Tunnelmikroskop

Rastertunnelmikroskop

Das Rastertunnelmikroskop (abgekürzt RTM, oder STM von englisch scanning tunneling microscope) ist ein Mikroskop, das in der Oberflächenphysik und Oberflächenchemie eingesetzt wird, um die Oberfläche einer Probe abzubilden. Die Rastertunnelmikroskopie unterscheidet sich von den länger bekannten und verwendeten oberflächensensitiven Beugungsmethoden wie z. B. der Beugung langsamer Elektronen (LEED) dadurch, dass sie ein „reales“ Abbild der Probenoberfläche erzeugt (Abbildung im Ortsraum). Dadurch kann die Rastertunnelmikroskopie, im Gegensatz zu den Beugungsmethoden (die im inversen Raum abbilden), auch nicht-periodische, lokale Strukturen – wie z. B. Oberflächendefekte und Nanostrukturen – sichtbar machen.

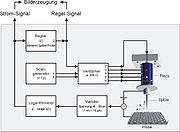
Bei der rastertunnelmikroskopischen Messung wird eine elektrisch leitende Spitze (auch Nadel) systematisch (in einem Raster) über das ebenfalls leitende Untersuchungsobjekt gefahren. Die Spitze und die Objektoberfläche sind dabei nicht in elektrischem Kontakt, und wegen des isolierenden Mediums dazwischen (Luft oder Vakuum) findet bei makroskopischem Abstand kein kontinuierlicher Stromfluss statt. Nähert man jedoch die Spitze der Oberfläche auf atomare Größenordnungen (Nanometer) an, so überlagern sich die quantenmechanischen Zustände der Elektronen (Orbitale) von Oberfläche und Spitze, so dass mit einer Wahrscheinlichkeit größer Null ein Austausch von Elektronen auftritt, was bei Anlegen einer kleinen Spannung zu einem Tunnelstrom (Tunneleffekt) führt. Dieser Tunnelstrom ist sehr empfindlich auf kleinste Abstandsänderungen, da die Intensität negativ exponentiell mit dem Abstand skaliert. Beim Abrastern der Probenoberfläche wird die Höhe der Spitze mittels einer Feinmechanik (Piezoelemente) so geregelt, dass der Tunnelstrom entlang der Bewegung konstant bleibt. Damit fährt die Spitze ein „Höhenprofil“ der Oberfläche nach, wobei das Höhen-Regelsignal zur Darstellung der Probenoberfläche benutzt wird. Die Rastertunnelmikroskopie ist ein indirektes Abbildungsverfahren, da das Gesamtbild einer Messung aus den an jedem Rasterpunkt gemessenen und in Graustufen umgerechneten Werten des Höhen-Regelsignals zusammengesetzt wird.

Funktionsprinzip des STM

Da das Prinzip der Rastertunnelmikroskopie auf der Messung eines Stromflusses zwischen der Probe und der Spitze des Rastertunnelmikroskops beruht, können nur elektrisch leitende Proben (Metalle, Halbleiter oder Supraleiter) direkt untersucht werden. Nicht leitende Proben zeigen zwar ebenfalls Tunnelphänomene, der Tunnelstrom kann jedoch nicht durch die Probe an die Gegenkathode gelangen und gemessen werden. Daher müssen sie vorher mit einer feinen elektrisch leitenden Schicht bedampft werden (Graphit, Chrom oder Gold), welche am Rand der Probe Kontakt zur Probenhalterung hat. Eine weitere Möglichkeit ist die Untersuchung sehr dünner Schichten eines Isolators auf einem leitenden Substrat.

Die durch konstanten Tunnelstrom gewonnenen Abbildungen entsprechen allerdings nicht zwangsweise der Topographie der Oberfläche. Vielmehr wird hierbei vorrangig die elektronische Struktur der Oberfläche abgetastet. Alternativ kann auch der Abstand der Spitze zur Oberfläche konstant gehalten werden, und durch die Variation des Tunnelstromes eine Rekonstruktion der Oberfläche aufgezeichnet werden. Letztere Methode ist empfindlicher auf elektronische Oberflächeneffekte als auf geometrische, und durch den Vergleich beider Bilder kann die Abweichung Topographie – Elektronenstruktur abgeschätzt werden.

Experimentelle Randbedingungen

STM-Messung der Rekonstruktion der (100)-Fläche eines Au-Einkristalls

STM-Aufnahme einer Graphitoberfläche in atomarer Auflösung.

STM-Aufnahme von selbstassemblierten Molekülketten

Rastertunnelmikr. Aufnahme von Verunreinigungen einer Eisenkristall-Oberfläche mit Chromatomen (kleine Spitzen)

Aufgrund des sehr kleinen Abstandes zwischen Spitze und Probenoberfläche von etwa 1 nm (Nanometer) muss ein Rastertunnelmikroskop in der Regel gegenüber der Umwelt schwingungsisoliert werden. Dies geschieht meist mit einer Kombination aus einem Federsystem und einer Dämpfung (oft in Form einer Wirbelstrombremse). Ferner sind Temperaturschwankungen zu vermeiden, da diese Verzerrungen und Längenänderungen im Aufbau bewirken (Drift), die schnell mehr als 1 nm betragen können. Auch eine elektromagnetische Abschirmung gegenüber der Umwelt ist aufgrund der oft nur 10 bis 1000 pA (Picoampere) betragenden Tunnelströme notwendig.

Die Tunnelspannungen zwischen Spitze und Probe betragen in der Regel wenige bis zu einigen 100 mV bei Metallen, Halbmetallen und Supraleitern und einige Volt bei Halbleitern. Bei der Untersuchung von selbstassemblierten organischen Adsorbatschichten auf Halbmetallen sind Tunnelspannungen um 1 Volt in Verbindung mit Tunnelströmen zwischen 100 und 500 pA zu empfehlen, da bei niedrigeren Spannungen bzw. höheren Strömen der Spitze-Probe-Abstand so gering und damit die elektrostatischen Wechselwirkungen zwischen Spitze und Adsorbatschicht so hoch werden, dass die Schicht beim Rastern zerstört wird (siehe Objektveränderung).

Sowohl die zu untersuchende Oberfläche als auch die benutzte Spitze müssen an der Oberfläche elektrisch leitend sein. Besteht die zu untersuchende Oberfläche aus Metallen, die an Luft oxidieren können (z. B. Kupfer, Silizium oder Silber), ist die Rastertunnelmikroskopie im Ultrahochvakuum durchzuführen, was einen nicht zu unterschätzenden technischen Aufwand bedeutet. Als Oberflächen, die dagegen unter Normalbedingungen verwendet werden können, kommen leitfähige Schichtkristalle wie Graphit oder Vertreter der schichtkristallinen Übergangsmetall-Dichalkogenide wie Molybdändisulfid (MoS₂), Tantaldisulfid (TaS₂) oder Tantaldiselenid (TaSe₂) in Frage. Eine frische, atomar glatte Oberfläche lässt sich bei diesen Schichtkristallen einfach durch Abziehen der obersten Schichten mit einem Klebeband erreichen, da die einzelnen Schichten nur über relativ schwache Van-der-Waals-Wechselwirkungen verbunden sind.

Die Bewegung der Spitze relativ zur Probenoberfläche wird mit Hilfe von piezoelektrischen Keramiken bewerkstelligt. Diese lassen eine hochpräzise Kontrolle im Sub-Nanometer-Maßstab über angelegte elektrische Spannungen zu.

Theorie

Der Tunneleffekt im Vakuum zwischen zwei Metallen, die durch eine dünne Oxidschicht separiert sind, wurde 1961 von John Bardeen mit Hilfe der zeitabhängigen Störungstheorie erster Ordnung (Fermis Goldene Regel) erklärt^[1]. Überträgt man diese Theorie auf die Rastertunnelmikroskopie, so ist eine atomar genaue Kenntnis der Spitze notwendig, um die gemessenen Bilder zu interpretieren. Eine wesentliche Vereinfachung stellt die sogenannte Tersoff-Hamann-Theorie^[2] dar, die den Einfluss der Spitze auf die Messung vernachlässigt und Aussagen über die elektronische Struktur der Probe liefert. Die Spitze wird dabei als ein Metallatom mit linearer elektronischer Zustandsdichte und kugelsymmetrischen s-Wellenfunktionen angenommen. Eine Erweiterung dieser Theorie lieferte C. Julian Chen^[3], der komplexere Spitzengeometrien berechnete. Eine wirklich dreidimensionale Theorie zum Rastertunnelmikroskop ist zwar analytisch aufstellbar, jedoch in der Regel kaum lösbar und damit von untergeordneter Bedeutung. Dreidimensionale Systeme können nur näherungsweise numerisch berechnet werden, meist unter der Zuhilfenahme mehrerer abgeschätzter Parameter. Simulationen von STM-Bildern von organischen Molekülen auf Oberflächen sind durch Überlagerungen von besetzten bzw. unbesetztes Molekülorbitalen der Moleküle im Vakuum möglich, die man z.B. aus der Dichtefunktionaltheorie (Quantenphysik) erhält.

Mess-Modi

Ein Rastertunnelmikroskop arbeitet mit einem Abstand der Spitze von der Probe bzw. mit einer Auflösung, die geringer als die Wellenlänge der Tunnelelektronen (vergleiche Materiewellen und De-Broglie-Gleichung) sind. Wird eine elektrische Spannung (englisch bias oder tunneling bias) zwischen dem Untersuchungsobjekt und der Spitze angelegt, so kann ein Strom, der so genannte Tunnelstrom fließen.

Den drei im folgenden beschriebenen Methoden (CHM, CCM und STS-Bilder mit Ausnahme der Punktspektroskopie) ist gemein, dass die Messspitze linienhaft über die Probe bewegt wird, bevor sie seitlich versetzt eine benachbarte Linie erfasst. Hieraus ergibt sich ein Linienraster auf der Oberfläche.

Modus konstanter Höhe

Die Höhe der Spitze wird konstant gehalten, der Tunnelstrom variiert. Es besteht Crash-Gefahr durch große Strukturen.

(constant height method, abgekürzt CHM)

Die absolute Höhe der Spitze über der Probe wird nicht verändert. Da die Stärke des Tunnelstroms sehr stark (exponentiell) vom Abstand der Nadel zum Objekt abhängt, lässt sich für jeden Rasterpunkt so der Abstand der Nadel zum Objekt rekonstruieren, wodurch ein dreidimensionales Bild des Objektes hergestellt wird. Das ist nur für im Wesentlichen flache Proben möglich. Allerdings ermöglicht dieser Modus ein sehr schnelles Abrastern der Probenoberfläche. Dies ist für die Erstellung von zeitaufgelösten Filmen von Veränderungen an der Probenoberfläche wichtig. Ansonsten hat dieser Modus kaum praktische Bedeutung.

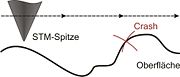
Neben dem Aufsetzen der Spitze hat die Methode der konstanten Höhe den Nachteil, dass sich die Spitze bei Vertiefungen soweit entfernen kann, dass der Strom nicht mehr messbar ist. Im Falle von Bergen auf der Oberfläche rammt die Spitze meist in die Probenoberfläche und wird dadurch zerstört. Der Vorteil dabei ist jedoch, dass der Abstand nicht nachgeführt werden muss und damit schnelle Aufnahmen möglich sind (Video-RTM). Bei statischen Proben ist es sinnvoller, den Abstand beim Rastern so zu variieren, dass der Tunnelstrom konstant bleibt (CCM).

Modus konstanten Tunnelstroms

Der Tunnelstrom wird konstant gehalten,die Spitze folgt der Oberfläche.

(constant current method, abgekürzt CCM oder constant gap width mode, abgekürzt CGM)

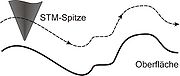
Eine andere Methode der Abbildung beruht darauf, die Höhe der Spitze fortlaufend so zu verändern, dass der Strom konstant bleibt. Dies geschieht über einen elektronischen Regelkreis zur Abstandsregelung. Somit lässt sich nun über die Position der Spitze das dreidimensionale Bild der Oberfläche direkt bestimmen. Die Auflösung ist bei diesem Verfahren so hoch, dass die atomare elektronische Struktur der Oberfläche sichtbar wird. Der Bildkontrast darf jedoch nicht direkt als atomare Struktur verstanden werden. Inzwischen sind mindestens neun verschiedene Kontrastmechanismen bekannt, die die Bildentstehung beeinflussen und bei der Interpretation beachtet werden müssen. Allerdings ist die Methode durch den Regelkreis in ihrer Messgeschwindigkeit begrenzt, die Aufnahme eine Bildes dauert in der Regel mehrere zehn Sekunden bis zu Stunden. In der Praxis wird meistens dieser Modus benutzt.

Die Breite einer Tunnelbarriere kann über die heisenbergsche Unschärferelation abgeschätzt werden. Betrachtet man ein Elektron mit der Masse m_e, welches eine Potentialdifferenz U durchtunnelt, so ergibt sich für die Ortsunschärfe und somit die minimale Breite der Tunnelbarriere

$\Delta x \geq \frac{\hbar}{\sqrt{8 m_e e U}}$.

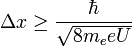Bei einer Potentialdifferenz von 100 mV, wie sie bei der Rastertunnelmikroskopie typischerweise vorkommt, ergibt sich aufgrund dieser Beziehung eine kleinste Tunnelbarriere von etwa 0,3 nm, was sich gut mit experimentellen Beobachtungen deckt.

Spektroskopiemodus

Siehe auch Rastertunnelspektroskopie (STS) (englisch: scanning tunneling spectroscopy).

Da man mit dem Rastertunnelmikroskop, über den Tunneleffekt vermittelt, zunächst die lokale elektronische Struktur der Probenoberfläche misst, kann man es auch direkt zur Bestimmung dieser ausnutzen. Zum Beispiel erscheint ein einzelnes Sauerstoffatom auf einer Oberfläche des Halbleitermaterials Galliumarsenid mal als Mulde und mal als Hügel, je nachdem, ob man positive oder negative Spannung zwischen Spitze und Probe anlegt.

Man kann das ausnutzen, um entweder die energetischen Lagen der Oberflächenzustände an einem Ort der Probe (TS-Spektren an einem Ort, sogenannte Punktspektroskopie) oder die Orte an denen sich Elektronen bei einer bestimmten Energie (entspricht der Tunnelspannung) aufhalten dürfen (STS-Bilder bei konstanter Tunnelspannung) zu bestimmen. Man muss dazu der Tunnelspannung eine kleine hochfrequente Wechselspannung überlagern und kann dann aus der Ableitung des Stromes nach der Spannung die so genannte Zustandsdichte errechnen. Die Rastertunnelspektroskopie wird oft bei tiefen Temperaturen von wenigen Kelvin durchgeführt, da die energetische Auflösung über die Fermi-Verteilung von der Temperatur abhängt. Der Spektroskopiemodus ist weiterhin in diverse Untermodi unterteilt.

Video-Rastertunnelmikroskopie

Bei Scanraten ab einem Bild pro Sekunde spricht man von Video-Rastertunnelmikroskopie. Die Bildrate geht dabei bis zu 50 Hertz. Mit dieser Methode können je nach System Diffusionsprozesse in Echtzeit beobachtet werden^{[4] [5]}.

Line-Scan

Beim Scannen in einer Linie über einer Phasengrenze oder atomaren Stufe, die sich im dynamischen Gleichgewicht mit ihrer Umgebung befindet, kann man sogenannte Pseudobilder (auch: x-t scan) messen. Aus diesen Messdaten, bei denen die x-Achse eine zeitliche Angabe und die y-Achse eine Ortsangabe ist, kann man wiederum die Stufenkorrelationsfunktion berechnen, aus der sich Informationen über die Diffusionsprozesse an der entsprechenden Stelle ergeben.

Objektveränderung

Eine weitere Anwendung des Rastertunnelmikroskops ist die gezielte Veränderung eines Objektes. Hierbei wird die Nadel an die gewünschte Stelle des Objektes gebracht. Durch Anlegen einer (im Vergleich zur Abbildungsrasterung) hohen Spannung kann man nun Atome aus der Oberfläche lösen und an die Spitze kleben. Wird die Spitze nun von der Probe weggezogen, so reißt das Atom aus der Oberfläche heraus. An der neuen Position kann es anschließend durch ein sehr kurzes Anlegen einer hohen Spannung wieder abgelegt werden. Weiterhin gibt es auch die Möglichkeit des Schubsens oder Mitziehens von einzelnen Atomen oder Molekülen auf der Oberfläche durch geeignete, meist hohe Tunnelspannungen an der Spitze. Mit Hilfe dieser Methoden wurde das so genannte atomare Schreiben durchgeführt, das Schriftzüge wie IBM, Logos einzelner Hochschulen oder Landkartenskizzen mit einzelnen Atomen auf Oberflächen darstellt.

Auf dem Gebiet der Magnetischen Datenspeicherung hat IBM ein Scanning-Tunnelmikroskop entwickelt, das bei sehr niedrigen Temperaturen funktioniert (~4 K). Damit sollen erfolgreiche Versuche durchgeführt worden sein, einzelne Atome in ihrer Spin-(magnetischen)-Ausrichtung in einer Magnetschicht zu verändern und gezielt zu beeinflussen. Die Methode wird Spin-Anregungs-Spektroskopie (Spin-Excitation-Spektroskopie) genannt. (Science Express. 2006, 4)

Forschungsgeschichte

Das erste erfolgreiche Experiment zum Nachweis eines abstandsabhängigen Tunnelstromes konnte am 18. März 1981 im IBM-Forschungslabor in Rüschlikon (CH) durchgeführt werden. Die beiden Physiker Gerd Binnig (Deutschland) und Heinrich Rohrer (Schweiz), die das Experiment durchführten und das Rastertunnelmikroskop letztlich auch zum einsetzbaren Instrument machten, erhielten hierfür 1986 den Nobelpreis für Physik. Ferner waren auch Christian Gerber und E. Weibel an der Entwicklung beteiligt.

Es gibt aber schon frühere Arbeiten auf diesem Gebiet, in denen die wesentlichen Aspekte eines RTM/STM demonstriert wurden – insbesondere das Auftreten eines Tunnelstromes. Dieses Gerät wurde von Russel Young, John Ward und Fredric Scire Ende der 1960er Jahre als sog. Topografiner^[6] entwickelt. Es gab jedoch bürokratische und technische Schwierigkeiten, beispielsweise störten die Vibrationen der Klimaanlage die Messungen. Das Nobelpreiskomitee erkannte jedoch später ihre Leistungen an.

Das Rastertunnelmikroskop ist der Vater aller anderen Rastersondenmikroskope mit Ausnahme des Rasterelektronenmikroskops. In der Folgezeit wurden vor allem das Rasterkraftmikroskop (AFM für atomic force microscope) und das optische Rasternahfeldmikroskop (SNOM für scanning near-field optical microscope) entwickelt, welche sich einer anderen atomaren Wechselwirkung bedienen. Die Entwicklung aller dieser Rastersondenmikroskope war ein wesentlicher Schritt in Richtung der Nanowissenschaften, da man mit ihnen auf recht einfache und vergleichsweise preiswerte Art und Weise nanoskopische Objekte (Objekte, die kleiner sind als die Lichtwellenlänge von 400 bis 800 nm) beobachten und darüber hinaus auch manipulieren kann.

Ferner hat die Rastertunnelmikroskopie wesentlich zur Veranschaulichung der Quantenmechanik beigetragen. Anfang der 1990er Jahre wurden sogenannte Quantum Corrals erzeugt und gemessen. Quantum Corrals sind einfache geometrische Quantensysteme auf Oberflächen. Anhand dieser Quantum Corrals konnte extrem anschaulich die Analogie zwischen Elektronenwellen und Wasserwellen dargestellt werden, was eine bis dahin nicht vorhandene direkte Bestätigung der Quantenmechanik im Realraum ist. Die Abbildungen dieser Quantum Corrals gehen inzwischen um die Welt: Sie sind die meist-dargestellten STM-Bilder in Büchern und darüber hinaus auch in Tageszeitungen zu finden. Solche Bilder, ihre Interpretation und Wirkung sind inzwischen sogar Forschungsgegenstand der Bildwissenschaften (vergleiche Horst Bredekamp) und der Kunstgeschichte.

Einzelnachweise

1. ↑ J. Bardeen: Tunnelling from a many-particle point of view. In: Physical Review Letters. 6 (2), 1961, S. 57–59.
2. ↑ J. Tersoff, D. Hamann: Theory of the scanning tunneling microscope. In: Physical Review B. 31, 1985, S. 805–813.
3. ↑ C. J. Chen: Origin of Atomic Resolution on Metal Surfaces in Scanning Tunneling Microscopy. In: Physical Review Letters. 65 (4), 1990, S. 448–451.
4. ↑ Hochgeschwindigkeits-Rastertunnelmikroskopie (Video-STM)
5. ↑ Organische Moleküle abgebildet mit Video-STM (englisch)
6. ↑ Siehe das letzte der folgenden Zitate

Literatur

• Gerd Binnig und Heinrich Rohrer: Gerät zur rasterartigen Oberflächenuntersuchung unter Ausnutzung des Vakuum-Tunneleffekts bei kryogenischen Temperaturen. Europäische Patentanmeldung 0 027 517, Priorität: 20. September 1979 CH 8486 79.
• Gerd Binnig, Heinrich Rohrer, C. Gerber und E. Weibel: Tunneling through a Controllable Vacuum Gap. In: Appl. Phys. Lett. 40, 1982, S. 178.
• G. Binnig, H. Rohrer, Ch. Gerber, E. Weibel: Surface Studies by Scanning Tunneling Microscopy. In: Physical Review Letters. 49, 1982, S. 57.
• G. Binnig, H. Rohrer, Ch. Gerber, E. Weibel: 7 × 7 Reconstruction on Si(111) Resolved in Real Space. In: Phys. Rev. Lett. 50, 1983, S. 120–123.
• C. Hamann, M. Hietschold: Raster-Tunnel-Mikroskopie. Akademie Verlag, Berlin 1991, ISBN 3-05-501272-0.
• C. Julian Chen: Introduction to Scanning Tunneling Mircoscopy. Oxford University Press, Oxford 1993, ISBN 0-19-507150-6. (englisch)
• Roland Wiesendanger: Scanning Probe Microscopy and Spectroscopy – Methods and Applications. Cambridge University Press, Cambridge 1994, ISBN 0-521-42847-5. (englisch)
• Russell Young, John Ward, Fredric Scire: The Topografiner. An Instrument for Measuring Surface Microtopography. In: Review of scientific instruments, with physics news and views. American Institute of Physics, Lancaster PA, 43, 1972, S. 999. ISSN 0034-6748

Weblinks

• Rasterelektronenmikroskop filmt Rastertunnelmikroskop beim Scannen (MPG, AVI)
• Rastertunnelmikroskop im Eigenbau
• Video-Rastertunnelmikroskopie von großen organischen Molekülen (englisch)
• Zooming in Nanometerstrukturen (Animation aus STM-Bildern)
• STM builds a molecule
• Links zum Thema Hersteller von Rastertunnelmikroskopen (englisch) im Open Directory Project