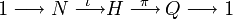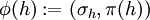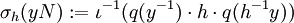U+2240

≀_X

Das Kranzprodukt (engl. wreath product) ist ein Begriff aus der Gruppentheorie und bezeichnet ein spezielles semidirektes Produkt von Gruppen.

Definition

Sind G und J Gruppen und operiert J auf einer Menge Y, so wird dadurch eine Operation von J auf G^Y (der Gruppe aller Abbildungen von Y nach G mit punktweise Verknüpfung) induziert durch:

$\forall j\in J, f\in G^Y: (^jf)(y)=f(^{j^{-1}}y)$

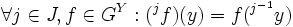
Jedes 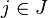$j\in J$ definiert auf diese Weise einen Automorphismus von G^Y.

Somit kann das Kranzprodukt 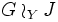$G \wr_Y J$ als das semidirekte Produkt aus G^Y und J bezüglich ebendieser Operation definiert werden.

Eigenschaften

Aus der Definition lässt sich sofort die Kardinalität von Kranzprodukten ableiten: $\left|G \wr_Y J\right|=\left|G\right|^{\left|Y\right|}\cdot\left|J\right|$

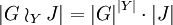
Da jede Gruppe auf sich selbst durch Linksmultiplikation operiert, ist es auch oft so, dass nur das entsprechende Kranzprodukt 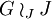$G \wr_J J$ definiert wird. Ebenso üblich ist es, Y als endliche Menge {1,...,n} festzusetzen und für J nur Untergruppen von Sym(n) mit der kanonischen Operation auf Y zuzulassen.

Operationen

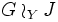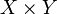Operiert G auf einer Menge X, so wird dadurch und durch die Operation von J auf Y eine Operation von $G \wr_Y J$ auf $X\times Y$ induziert: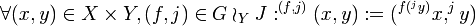

$\forall (x,y)\in X\times Y, (f,j)\in G \wr_Y J: ^{(f,j)}(x,y):=(^{f(^jy)}x,^jy)$

Diese Operation ist genau dann treu/transitiv wenn die Operationen von G auf X und J auf Y treu/transitiv sind.

Gruppenerweiterungen

Ist H eine Erweiterung von N durch Q, so lässt sich H als eine Untergruppe eines Kranzprodukts aus N und Q darstellen. Dies ist vielleicht eine der wichtigsten Eigenschaften von Kranzprodukten, da jede endliche Gruppe durch Erweiterungen einfacher endlicher Gruppen darstellbar ist.

Gegeben ist also eine exakte Sequenz

$1\longrightarrow N \longrightarrow^{\!\!\!\!\!\!\!\!\!\iota}\ \, H \longrightarrow^{\!\!\!\!\!\!\!\!\!\pi}\ \, Q \longrightarrow 1$

Außerdem sei eine Abbildung 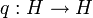$q:H\to H$ gegeben, die 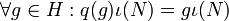$\forall g\in H:q(g)\iota(N)=g\iota(N)$ erfüllt und jedem Element einen festen Repräsentanten seiner jeweiligen Nebenklasse zuordnet. Weiterhin muss gelten 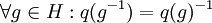$\forall g\in H:q(g^{-1})=q(g)^{-1}$. (Ist N unendlich, so ist eine solchen Funktion möglicherweise nur mit dem Auswahlaxiom zu finden)

Die Einbettung 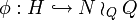$\phi:H\hookrightarrow N\wr_Q Q$ (Q operiert auf sich selbst durch Linksmultiplikation) ist dann gegeben durch:

$\phi(h):=(\sigma_h,\pi(h))\,$

Hierbei ist 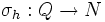$\sigma_h:Q\to N$ wie folgt definiert:

$\sigma_h(yN):=\iota^{-1}(q(y^{-1})\cdot h\cdot q(h^{-1}y))$

Diese Einbettung geht zurück auf L.Kaloujnine und M.Krasner^[1].

Beispiele

Die p-Sylowgruppen der Symmetrischen Gruppe S_n lassen sich als iterierte Kranzprodukte zyklischer Gruppen darstellen.

Dazu definiert man rekursiv eine Folge von Gruppen durch W_p,0: = {1} und $W_{p,n+1}:=W_{p,n} \wr_{\mathbb{Z}_p} \mathbb{Z}_p$ wobei die Operation von 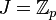$J=\mathbb{Z}_p$ auf $Y=\mathbb{Z}_p$ durch Linksmultiplikation gegeben ist.

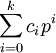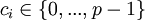Stellt man n zur Basis p dar, d. h. als Summe $\sum_{i=0}^{k}{c_ip^i}$ mit $c_i\in\{0,...,p-1\}$, so sind die p-Sylowgruppen von S_n dann isomorph zu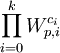 $\prod_{i=0}^{k}{W_{p,i}^{c_i}}$

Zum Symbol

Die senkrechte Tilde, die für das Kranzprodukt verwendet wird, befindet sich im Unicode-Block Mathematische Operatoren auf Positition U+2240^[2], in TeX und LaTeX kann es mit \wreath bzw. \wr dargestellt werden.

Quellen

1. ↑ "Produit complet des groupes de permutations et probleme d’extension de groupes", L. Kaloujnine, M. Krasner - I, Acta Sci. Math. Szeged, 1950
2. ↑ Unicode Character 'WREATH PRODUCT' (U+2240), fileformat.info