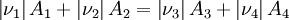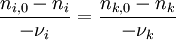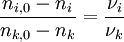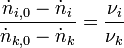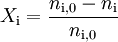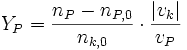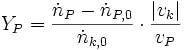Umsatzgrad

Die Stöchiometrie (von gr. στοιχειον, „Grundstoff“ und μετρειν, „messen“) ist ein grundlegendes mathematisches Hilfsmittel in der Chemie und dient der Berechnung von quantitativen Informationen, die aus einer Reaktionsgleichung gewonnen werden können.

Grundlagen

Die Berechnungsgrundlagen der modernen Stöchiometrie basieren (auch historisch betrachtet) auf folgenden Gesetzen:

• Gesetz der konstanten Proportionen
• Gesetz der multiplen Proportionen
• Massenerhaltungssatz

Die Gesetze der Stöchiometrie leiten sich also aus dem Wissen über den Aufbau der Materie aus Atomen und Molekülen her.

Begriffe

Stöchiometrische Bilanz

Bei den stöchiometrischen Rechnungen geht es darum, die Menge an Ausgangsstoff, Edukt(en), zu berechnen, die bei einer chemischen Reaktion eingesetzt werden muss. Die Berechnung lässt sich umkehren, so dass man bei Kenntnis der Menge an Edukt(en) die Menge an Produkt(en) bestimmen kann.

Um jede beliebige Reaktion bilanzieren zu können, wird zu einer allgemeineren Symbolschreibweise übergegangen. Für eine einfache chemische Reaktion lautet sie beispielsweise:

$\left| \nu_1 \right| A_1 + \left| \nu_2 \right| A_2 = \left| \nu_3 \right| A_3 + \left| \nu_4 \right| A_4$

• wobei ν_i die stöchiometrische Verhältniszahlen (auch stöchiometrische Koeffizienten genannt) sind.

Da sich für eine Reaktion unterschiedliche Reaktionsgleichungen aufstellen lassen

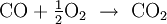($\mathrm{CO} + \tfrac {1}{2} \mathrm O_2 \ \to \ \mathrm{CO}_2$ oder $2 \, \mathrm{CO} + \mathrm{O}_2 \ \to \ 2 \, \mathrm{CO}_2$),

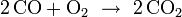müssen vor der Bilanzierung die stöchiometrische Verhältniszahlen festgelegt werden. Dabei gilt:

• Edukte bekommen immer eine negative stöchiometrische Verhältniszahl
• Produkte eine positive stöchiometrische Verhältniszahl
• und Begleitstoffe (Stoffe, die nicht an der Reaktion teilnehmen) bekommen eine stöchiometrische Verhältniszahl von 0

Bei der Reaktion verändern sich die Mengenanteile (genauer die Molenbrüche (n)) der Reaktanten in dem Maße, wie die stöchiometrischen Verhältniszahlen es vorgeben. Die stöchiometrische Bilanz für die Reaktanten i und k ergibt sich als:

${n_{i,0} - n_i \over -\nu_i} = {n_{k,0} - n_k \over -\nu_k}$

Durch einfache Umformung erhält man für den Satzbetrieb

${n_{i,0} - n_i \over n_{k,0} - n_k} = {\nu_i \over \nu_k}$

und entsprechend für den Fließbetrieb

${\dot n_{i,0} - \dot n_i \over \dot n_{k,0} - \dot n_k} = {\nu_i \over \nu_k}$

Umsatz (X_i)

Dies ist ein Begriff aus der chemischen Reaktionstechnik und beschreibt, wie viel Edukt bei einer Reaktion reagiert. Mit dem Umsatz(grad) wird angegeben, welcher Anteil eines Ausgangsstoffes beim Verlassen des Reaktors in andere chemische Stoffe durch chemische Reaktion umgewandelt wurde. Etwas mathematischer ausgedrückt: Der Umsatz ist der Anteil der umgesetzten Menge einer Komponente i bezogen auf die eingesetzte Menge n_i,0

$X_\mathrm{i} ={ n_\mathrm{i,0} - n_\mathrm{i} \over n_\mathrm{i,0} }$

• wobei n_i die noch vorhandene Menge der Komponente i ist

Sind mehrere Ausgangsstoffe beteiligt, so wird der Umsatzgrad per Konvention für denjenigen Stoff angegeben, der limitierend ist bzw. im Unterschuss vorliegt.

Ausbeute

Die Ausbeute ist ein Begriff aus der chemischen Reaktionstechnik. Mit der Ausbeute (Y) wird angegeben, welcher Anteil eines Eduktes beim Verlassen des Reaktors in das gewünschte Produkt (P) durch chemische Reaktion umgewandelt wurde. Sind mehrere Edukte beteiligt, so wird die Ausbeute bezogen auf die Leitkomponente (k) angegeben. Die Leitkomponente ist per Konvention derjenige Stoff, der nicht im Überschuss vorliegt.

Für einen Satzbetrieb gilt:

$Y_P = {n_P - n_{P,0} \over n_{k,0}} \cdot {\left| v_k \right| \over v_P}$

Für einen Durchflussbetrieb gilt entsprechend:

$Y_P = {\dot n_P - \dot n_{P,0} \over \dot n_{k,0}} \cdot {\left| v_k \right| \over v_P}$

Selektivität

Selektivität ist ein Begriff aus der chemischen Reaktionstechnik. Die Selektivität einer chemischen Umsetzung oder eines Reaktors gibt an, welcher Anteil des insgesamt umgesetzten Ausgangsproduktes unter Berücksichtigung der Stöchiometrie in das gewünschte Zielprodukt umgesetzt wurde. In der Regel setzen sich nicht alle Moleküle zu dem gewünschten Produkt um, da durch Folge oder Konkurrenzreaktionen andere Produkte entstehen können.

$S_p = {\mathrm{gebildete\;Menge}\,(k) \over \mathrm{umgesetzte\;Menge}\,(i)} = {(n_p - n_{p,0}) \cdot \left|v_k \right| \over (n_{k,0} - n_k) \cdot v_p} = {Y_p \over X_i}$

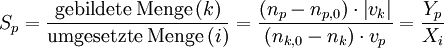
Umsatz, Ausbeute und Selektivität

Kombiniert man die Definitionen für Umsatz, Ausbeute und Selektivität miteinander, erhält man einen einfachen Zusammenhang der drei Größen:

$Y_P = X_i \cdot S_P$

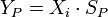
Das bedeutet, dass wenn es nur eine mögliche Reaktion gibt, ist S=1 und die Ausbeute X gleich dem Umsatz Y.

Es gilt ferner:

∑	S = 1
alleS

und:

∑	Y = X
alleY

Die „Anfangsgründe der Stöchiometrie“

Der Begriff der Stöchiometrie ist ursprünglich theologisch-alchemistischer Prägung, nachdem das grundlegende Hauptwerk „Anfangsgründe der Stöchiometrie“ von Jeremias Benjamin Richter, welches zwischen 1792 und 1794 in drei Bänden erschien, ein Werk der christlich-platonischen Naturtheologie (Physikotheologie) war und sich der Universalschemata der Weltseele in Platons Timaios bediente. Richter versuchte, mit Hilfe geometrischer, arithmetischer und triangularer Zahlenfolgen Stöchiometriegesetze zu definieren. Den Nachweis geometrischer Reihen in chemischen (stöchiometrischen) Verbindungen sah er dabei als christliche Gottesbeweise an, was er in seiner lateinischen Doktorarbeit als „Physicotheologiae probationes de existentia dei“ bezeichnete.

Aus den geometrischen Figuren Hexaeder, Tetraeder und Oktaeder bildete Richter, ähnlich den Planetenbahnen Johannes Keplers, Salz- und Schneekristalle in der Chemie nach und versuchte auf diese Weise, einen Zusammenhang zwischen der Form von Kristallen und der Form der Planeten-Umlaufbahnen zu charakterisieren.

Die Mathematisierung der Chemie, die man als „Stöchiometrie“ bezeichnet, sollte nach Richters Auffassung

• mit der Mathematisierung der Musik durch Platons Timaios und
• mit der Mathematisierung der Astronomie durch Keplers Weltharmonik

koordiniert und vernetzt werden, sodass zur Analyse eines chemischen Experimentes zugleich die Analyse der Planetenkonstellation stattfinden sollte, die zur Zeit des Chemie-Experimentes herrschte. Er glaubte, dass diese Planetenkonstellation über die von ihr ausgehenden Gravitationskräfte Einfluss auf das Resultat des chemischen Experimentes ausüben würde.

Das Werk Anfangsgründe der Stöchiometrie ist daher ein astro-chemisch, alchemistisch und spagyrisch geprägtes Werk, das starke Affinitäten

• zur platonischen Sphärenharmonie des Timaiosdialogs
• zur Spagyrik des Mediziners, Theologen und Philosophen Paracelsus und
• zur Astronomie von Kepler besitzt.

Da im Werk Anfangsgründe der Stöchiometrie chemische Experimente in eine mathematische Beziehung zu den Gravitationskräften der Planetenkonstellationen gesetzt wurden, soll jedes Chemieexperiment praktisch einmalig und nicht wiederholbar sein, weil sich die Planetenkonstellationen eine Stunde oder einen Tag nach dem ersten Experiment bereits geändert haben.

Den Begriff der „mathematischen Chemie“ soll wiederum Georg Helm mit seinem Buch Grundzüge der mathematischen Chemie im Jahr 1894 geprägt haben.

Literaturangaben

• Werner Kullbach: Mengenberechnungen in der Chemie. Verlag Chemie, Weinheim 1980, ISBN 3-527-25869-8
• Uwe Hillebrand: Stöchiometrie, Eine Einführung in die Grundlagen mit Beispielen und Übungsaufgaben, Springer-Verlag Berlin Heidelberg 2007, ISBN 978-3-540-36153-4

Weblinks