Ungerade Zahl

Eine ganze Zahl heißt gerade, wenn sie durch 2 teilbar ist; andernfalls heißt sie ungerade. In der Algebra und allgemein in der Mathematik wird dieses Charakteristikum als Parität bezeichnet. Das Konzept wird auch allgemeiner angewendet, die zugrunde liegende Menge wird dabei im Normalfall in zwei gleichmächtige disjunkte Teilmengen zerlegt (lateinisch: paritas „Gleichheit, gleich stark“).

Bei vielen Fragestellungen liefert die Parität eine hilfreiche Invariante und zählt zu den wichtigen Hilfsmitteln in der elementaren Zahlentheorie, zum Beispiel als Anwendung bei Permutationen, dem 15-Puzzle und dem Zauberwürfel. Die Begriffe gerade und ungerade und einfache Eigenschaften gerader und ungerader Zahlen werden schon in der Grundschule gelehrt.

Gerade und ungerade Zahlen

Definition

Eine natürliche oder ganze Zahl heißt gerade, wenn sie durch Zwei teilbar ist, ansonsten ungerade. Gerade Zahlen werden durch 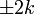$\pm 2k$ charakterisiert, ungerade Zahlen durch 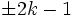$\pm 2k -1$ für beliebiges 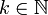$k\in \N$. Dementsprechend wird die Null als gerade angesehen.

Das heißt, ungerade Zahlen hinterlassen bei Division durch 2 stets einen Rest von 1, gerade Zahlen den Rest 0. Sie werden also durch ihre prime Restklasse modulo Zwei charakterisiert. Da ( − 1)⁰ = 1 und ( − 1)¹ = − 1 gilt, wird die Parität manchmal auch mit positivem oder negativem Vorzeichen symbolisiert, siehe auch: Paritätsbit. Allerdings ist es falsch, das Vorzeichen von positiven und negativen Zahlen als Paritätseinteilung zu verstehen.

Rechenregeln

Die Rechenregeln für Paritäten folgen den Gesetzen des Restklassenkörpers mit zwei Elementen. Dabei stehen null und eins für die entsprechenden Reste modulo 2 und damit für gerade oder ungerade. Insbesondere erhält Quadrieren die Parität.

Addition: + 0 1 0 0 1 1 1 0

Multiplikation: * 0 1 0 0 0 1 0 1

Im Dezimal-, Binär- und allgemein in jedem Stellenwertsystem mit gerader Basis erkennt man die Parität daran, ob die letzte Ziffer durch 2 teilbar ist.

Bemerkungen

• Die Hausnummern in vielen europäischen Städten laufen wechselseitig, so dass gerade und ungerade Nummern je auf einer Straßenseite liegen. Die Idee beruht auf der einfacheren Fortführung der Nummerierung bei einer späteren Verlängerung der Straße.

• Die geraden Zahlen bilden ein Ideal im Ring der ganzen Zahlen, die ungeraden tun dies nicht. Die geraden Zahlen sind die Folge A005843 in OEIS, die ungeraden sind die Folge A005408 in OEIS.

• Im Englischen wird die Zahl 2 manchmal als „the oddest prime“ bezeichnet. Dies ist ein Wortspiel mit den Bedeutungen merkwürdig und ungerade des Wortes odd, denn die Primzahl 2 ist eine besondere oder merkwürdige (odd) Primzahl, da sie als einzige nicht ungerade (odd) ist.

• Eine natürliche Zahl 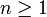$n \geq 1$ kann stets eindeutig als Produkt einer (geraden) Zweierpotenz und einer ungeraden Zahl u geschrieben werden: 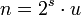$n= 2^s \cdot u$, wobei 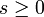$s \geq 0$ und $u \geq 1$

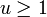
• Jede bisher bekannte vollkommene Zahl ist gerade. Ob ungerade vollkommene Zahlen überhaupt existieren, ist noch unbekannt.

• Euklids Beweis der Irrationalität der Wurzel aus 2 beruht zum großen Teil auf Paritätsvergleichen, bei der goldbachschen Vermutung spielt die Parität jedoch nur eine untergeordnete Rolle.

• Eulers geniale Leistung bei der Lösung des Königsberger Brückenproblem liegt in dem abstrakten Ansatz: Hat man erstmal verstanden, wie ein Stadtteil mit Wegen als Graph aufgefasst werden kann, so erkennt man leicht, dass ein geschlossener Rundgang über alle Wege nur dann existieren kann, wenn an jedem Punkt eine gerade Anzahl von Linien abgeht - denn jeden Punkt, den man verlässt, muss man über einen anderen Weg erreicht haben. Beim Königsberger Problem war dies nicht der Fall; ein geschlossener Weg ist dort nicht möglich. Auch dies zählt zu den klassischen Paritätsargumenten.

Parität in sonstigen mathematischen Zusammenhängen

Um die Parität von anderen mathematischen Objekten angeben zu können, muss mindesten eine sinnvolle Abbildung existieren, die jedem dieser Objekte eine ganze Zahl zuordnet. Insbesondere muss Division mit Rest möglich sein, für eine beliebige reelle Zahl lässt sich beispielsweise keine Parität angeben.

Dabei ist zweitrangig, mit welchen Begriffen eine Parität belegt wird, hauptsächlich geht es darum, dass man sie vergleichen kann und dass jedem Objekt genau eine Parität zugeordnet wird. Entsprechend nennt man zwei ganze Zahlen a und b von gleicher Parität, wenn ihre Differenz a - b gerade ist, andernfalls sind sie von verschiedener Parität.

So haben 15 und 33 die gleiche Parität (die Differenz 18 ist gerade), 3 und 20 jedoch eine unterschiedliche Parität (Differenz 17). Ob die Parität jeweils gerade oder ungerade ist, lässt sich auf diese Weise innerhalb eines Vergleichs nicht erkennen.

Permutationen

Permutationen bilden das prominenteste Beispiel für eine verallgemeinerte Anwendung der Parität. Jede Permutation lässt sich als Produkt von endlich vielen Transpositionen schreiben - allerdings nicht eindeutig, es lassen sich immer noch Transpositionen hinzunehmen, ohne dass sich das Produkt ändert. Betrachtet man aber die Anzahl der multiplizierten Transpositionen, so lässt sich beweisen: Jede Permutation ist immer Produkt einer entweder geraden oder einer ungeraden Anzahl von Transpositionen. Gemäß dieser Invarianz nennt man eine Permutation auch gerade oder ungerade.

Weiteres

• Der Beweis der Unlösbarkeit des originalen 15-Puzzles wird mit Hilfe einer Parität geführt, die letztendlich auf der Parität von Permutationen beruht. Mit ihr kann angegeben werden, inwieweit zwei Steine vertauscht sind oder nicht. Der gleiche Ansatz schließt bei dem Zauberwürfel alle Stellungen aus, bei denen nur zwei Kantensteine vertauscht wären.

• Die partielle Unterteilung einer Menge von Funktionen in gerade und ungerade Funktionen kann nur mit Einschränkungen als Parität dienen.
• Die Parität der Ordnung von Null- und Polstellen liefert schon einige Informationen, so kommt es bei ungeraden Null- oder Polstellen von reellwertigen Funktionen stets zu einem Vorzeichenwechsel.

• Eine Menge mit mehr als zwei Paritäten zu versehen wäre von der Wortbedeutung her denkbar, wird aber offenbar nicht praktiziert.

Siehe auch

• Boolesche Algebra
• Kongruenz (Zahlentheorie)
• Gerade und Ungerade

Literatur

• Günter Scheja, Uwe Storch: Lehrbuch der Algebra - Band 1. Vieweg+Teubner Verlag 1994, ISBN 3-519-12203-0

Weblinks

• Eric W. Weisstein: Parity auf MathWorld (englisch)