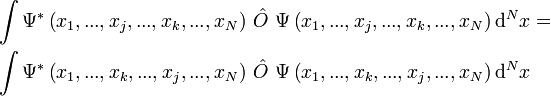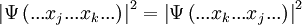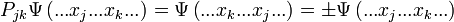Ununterscheidbarkeit

Ununterscheidbare Teilchen sind ein Begriff aus der Physik und dadurch gekennzeichnet, dass diese Teilchen sich in keiner Weise voneinander unterscheiden lassen. Ein System aus ununterscheidbaren Teilchen hat im Vergleich zu einem System aus gleich vielen unterscheidbaren Teilchen eine geringere Anzahl von Zuständen.

Ununterscheidbarkeit in der statistischen Physik

In der statistischen Physik ist die Ununterscheidbarkeit ein wichtiger Punkt, welcher bei der Zählung der Zustände eines Systems berücksichtigt werden muss. Scheinbar verschiedene Zustände, bei denen lediglich Teilchen gegeneinander vertauscht wurden, sind in Wirklichkeit immer ein und derselbe Zustand. Da es N! Möglichkeiten gibt, N Teilchen gegeneinander zu vertauschen, führt das Prinzip der Ununterscheidbarkeit zu einem zusätzlichen Faktor 1 / N! in der Zustandssumme.

Illustration zum beschriebenen Gedankenexperiment. Zwei Teilchen stoßen in einer Box. Die linke Seite zeigt den Ausgang, wenn die Teilchen unterscheidbar sind, die rechte Seite den Fall für ununterscheidbare Teilchen.

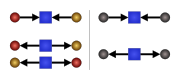
Zum besseren Verständnis kann man folgendes Gedankenexperiment durchspielen. Zwei Teilchen fliegen in eine von außen nicht einsehbare Box, in der sie zusammenstoßen und dadurch ihre Flugrichtung ändern. Der Einfachheit halber sei angenommen, dass die Teilchen die Box anschließend an gegenüberliegenden Seiten verlassen. Unterscheiden sich die Teilchen, so gibt es zwei mögliche Szenarien („Zustände“): Entweder verlässt Teilchen 1 die Box auf der linken und Teilchen 2 auf der rechten Seite oder umgekehrt. Sind die Teilchen hingegen ununterscheidbar, so kann man Teilchen 1 und Teilchen 2 nicht mehr auseinander halten. Daher gibt es nur noch einen möglichen Ausgangswert, nämlich dass das eine Teilchen die Box auf der linken und das andere die Box auf der rechten Seite verlässt.

Ununterscheidbarkeit in der Quantenmechanik

In der Quantenmechanik hat die Ununterscheidbarkeit eine erweiterte Bedeutung. Hier werden sowohl einzelne Teilchen, wie auch das gesamte System durch Wellenfunktionen beschrieben. Bei gleichartigen Teilchen gilt wie in der statistischen Physik, dass das Vertauschen zweier Teilchen zu keinem neuen Zustand führen kann.

Ein System N ununterscheidbarer Teilchen ist definiert durch:

$\begin{align} & \int{\Psi ^{*}\left( x_{1},...,x_{j},...,x_{k},...,x_{N} \right)\,\hat{O}\ \Psi \left( x_{1},...,x_{j},...,x_{k},...,x_{N} \right)\operatorname{d}^{N}x}= \\ & \int{\Psi ^{*}\left( x_{1},...,x_{k},...,x_{j},...,x_{N} \right)\,\hat{O}\ \Psi \left( x_{1},...,x_{k},...,x_{j},...,x_{N} \right)\operatorname{d}^{N}x} \\ \end{align}$  

für alle Paare (j,k). 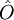${\hat{O}}$ sei eine beliebige Observable; folgende Kurzschreibweisen wurden verwendet:

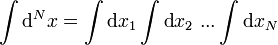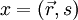$\int{\operatorname{d}^{N}x}=\int{\operatorname{d}x_{1}}\int{\operatorname{d}x_{2}}\ ...\int{\operatorname{d}x_{N}}$ ,   $x=(\vec r,s)$   und   $\int{\operatorname{d}x} =\sum\limits_{s}{{}}\int{d^{3}r}$

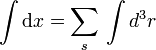
Insbesondere folgt aus obiger Definition, dass das Betragsquadrat der Gesamtwellenfunktion eines Systems aus ununterscheidbaren Teilchen unter Teilchenvertauschung invariant ist:

$\left| \Psi \left( ...x_{j}...x_{k}... \right) \right|^{2}=\left| \Psi \left( ...x_{k}...x_{j}... \right) \right|^{2}$

Jedoch folgt zusätzlich aus der Operatorformulierung der Quantenmechanik, dass die Wellenfunktion bei Vertauschung zweier Teilchen ein negatives oder ein positives Vorzeichen erhält. D. h. der Eigenwert des Transpositionsoperators P_jk ist 1 oder -1:

$P_{jk}\Psi \left( ...x_{j}...x_{k}... \right)=\Psi \left( ...x_{k}...x_{j}... \right)=\pm \Psi \left( ...x_{j}...x_{k}... \right)$

In einem System aus ununterscheidbaren Teilchen führt eine solche Vertauschung dabei immer zu dem gleichen Vorzeichen, egal welche Teilchen nun vertauscht werden. Wellenfunktionen, die immer ein negatives Vorzeichen erhalten, heißen total antisymmetrisch und die Teilchen des Systems nennt man Fermionen. Tritt dagegen immer ein positives Vorzeichen auf, so bezeichnet man die Wellenfunktion als total symmetrisch und die Teilchen als Bosonen.

Mathematisch kann man die Gesamtwellenfunktion eines Systems konstruieren, indem man sie als ein Produkt aus den Wellenfunktionen der einzelnen Teilchen schreibt. Um die Ununterscheidbarkeit der Teilchen zu berücksichtigen, muss dieses Produkt im Fall von Bosonen noch symmetrisiert bzw. im Fall von Fermionen antisymmetrisiert werden. Speziell bei Fermionen geschieht das mit Hilfe der so genannten Slater-Determinanten. Diese verschwindet jedoch, sollten zwei Fermionen die gleiche Wellenfunktion besitzen. Es kann damit keine Gesamtwellenfunktion bzw. kein Systemzustand existieren, bei denen zwei Fermionen den gleichen (Einteilchen-)Zustand einnehmen. Als logische Konsequenz müssen Fermionen immer in verschiedenen Zuständen sitzen. Dieses Prinzip wird als Paulisches Ausschlussprinzip bezeichnet. Eine derartige Einschränkung gibt es hingegen nicht in bosonischen Systemen. Bei tiefen Temperaturen sitzen Bosonen daher bevorzugt im energetisch tiefstmöglichen Zustand, was zu einem besonderen Systemzustand, dem so genannten Bose-Einstein-Kondensat, führt.

Siehe auch

• Identität
• Gibbssches Paradoxon
• Austauschentartung