V.34

Die Trellis-Code-Modulation, oder auch als Ungerboeck-Code, Trellis-Codierung, Trellis-Modulation, abgekürzt als TCM bezeichnet, ist eine in der digitalen Signalverarbeitung eingesetzte Kombination aus Kanalcodierung zur Vorwärtsfehlerkorrektur von Übertragungsfehlern und einer Modulationstechnik um digitale Informationen über elektrische Leitungen, wie beispielsweise Telefonleitungen, übertragen zu können.

Die Trellis-Code-Modulation wurde 1982 von Gottfried Ungerböck entwickelt ^[1] und fand in den Folgejahren in Telefonmodems, die nach den ITU-T-Standards V.32, V.32bis, V.34 und V.fast arbeiten, breite Anwendung ^[2]. Sie wird aber auch in neueren Übertragungssystemen verwendet und wird beispielsweise bei Gigabit Ethernet (1000Base-T) in Kombination mit einer 5-PAM Modulationstechnik eingesetzt. Aber auch bei den symmetrischen DSL-Zugängen nach den Standards G.SHDSL und SHDSL.bis findet der Trellis-Code in Kombination mit einer 16-PAM bzw. 32-PAM Anwendung.

Die Trellis-Code-Modulation ist eine sehr effiziente Kanalcodierung bzw. Modulationstechnik, die knapp am theoretischen Limit der Kanalkapazität liegt und je nach konkreter Implementierung nur knapp durch die erst einige Jahre später entwickelten Verfahren wie den Turbo-Codes (Turbo-Convolutional-Code und Turbo-Product-Code) und den Low-Density-Parity-Check-Code (LDPC) übertroffen wird.

Verfahren

Die Trellis-Code-Modulation zählt zu den codierten Modulationstechniken und unterteilt sich in zwei wesentliche Funktionsblöcke:

1. Der Kanalcodierung, der bei der TCM immer ein Faltungscode mit einer Coderate von (k,k+1) ist. Das heißt, das am Encodereingang aus einer Menge von k Nutzdatenbits durch den Faltungscoder ein Codewort der Länge k+1 gebildet wird. Das zusätzliche Redundanzbit des Codewortes ist dabei von den k Nutzdatenbits abhängig und dient im Rahmen der Decodierung der Fehlererkennung möglicher Übertragungsfehler. Es können bei der TCM verschiedene Typen von Faltungscoder eingesetzt werden, die sich in Länge und Art des Faltungscodierer, ob linear oder nichtlinear, unterscheiden.
2. Der digitalen Modulation auf einen Träger. Die Modulation kann eine QPSK, 8-PSK, 16-QAM, 64-QAM oder dergleichen mehr eingesetzt werden. Dabei werden die k+1 Bits des Codewortes genau einem Sendesymbol zugeordnet. Es ist folglich eine Modulation nötig, die aus 2^k+1 Symbolen besteht. Wird beispielsweise eine 64-QAM Modulation gewählt, es stehen dabei 64 Sendesymbole zur Verfügung, ergibt sich k zu 5 Nutzdatenbits, die pro Symbol zugleich übertragen werden können.

Der wesentliche Unterschied der Trellis-Code-Modulation zu anderen voneinander getrennten Kanalcodierungen und den Verfahren der digitalen Modulation besteht darin, dass die Kanalcodierung und die Modulation bei der TCM funktional fest miteinander verknüpft sind. Ein Codewort darf bei der TCM immer nur genau so lange sein, um als Ganzes einem Sendesymbol bei der Modulation zugeordnet werden zu können.

Eine Folge daraus ist, die erst den zusätzliche Codegewinn der Trellis-Code-Modulation ergibt, besteht darin, dass zur Bewertung möglicher Fehler nicht wie bei für sich alleine entworfenen Kanalcodierungsverfahren von dem minimalen Hamming-Abstand zwischen zwei Codewörtern ausgegangen werden kann. Sondern statt dessen von der euklidischen Distanz, die den geometrischen Abstand zweier Punkte in einer komplexen Ebene beschreibt. Diese Ebene wird durch die Amplitude und Phasenlage der Trägerschwingung aufgespannt und ordnet den Sendesymbolen einzelne Punkte in dieser Ebene zu.

Encoder

Am Encoder erfolgt die Zuordnung der einzelnen Bitkombinationen, aus dem ein Codewort gebildet ist, zu den jeweiligen Symbol für die Modulation. Statt einer wie bei anderen Modulationstechniken üblichen Zuordnung, beispielsweise über den Gray-Code, wählte Ungerböck eine Struktur, die in der Mathematik als binärer Baum bezeichnet wird. Dabei kommen im obersten Knoten, so werden die einzelnen Verzweigungspunkte in einem binären Baum bezeichnet, alle 2^k+1 Symbole als vor. Das niederwertige Bit des Codewortes wird als Entscheidung genommen um im binären Baum eine Stufe nach unten zu steigen: Je nachdem ob das betreffende Bit des Codewortes logisch-0 oder logisch-1 ist. Dadurch entstehen auf der darunter liegenden Ebene zwei Knoten, die jeweils die Hälfte der insgesamt möglichen Symbole umfassen.

Die Aufteilung der einzelnen Symbole wird so gewählt, dass sich der euklische Abstand zwischen benachbarten Symbolen maximiert. Bei einer 8-PSK Modulation mit 8 Symbolen am Einheitskreis werden Symbole mit geraden Index rechts und Symbole mit ungeraden Index links im binären Baum angeschrieben. In der meist englischsprachigen Literatur wird dieses Verfahren als set partitioning bezeichnet: In jeder Ebene erfolgt eine Aufteilung (Halbierung) der zur Verfügung stehenden Sendesymbole.

Danach wird mit den nächsten Bit aus dem Codewort nach gleichen Schema verfahren, so lange bis alle Codewortbits entsprechende Übergänge im binären Baum zugewiesen sind. Bei einem Faltungscode mit einem 3 Bit langen Codewort, also 2 Nutzdatenbits am Eingang, muss eine Modulation mit 8 Symbolen (2³) wie beispielsweise 8-PSK verwendet werden. Damit ergeben sich im binären Baum 3 Übergänge zwischen den Ebenen. Erst in der untersten Ebene findet sich die konkrete Zuordnung eines bestimmten Symbols, welches in diesem Beispiel von den 3 Bits eines Codewortes ausgewählt wird.

Die Besonderheit liegt darin, dass sich bei jedem Schritt um eine Ebene nach unten im binären Baum die euklidische Distanz zwischen noch verbleibenden Symbolen auf dieser Ebene vergrößert. Je größer der euklidische Abstand zwischen den einzelnen Symbolen ist, desto größer muss eine Störung am Übertragungskanal sein, um am Decoder zu einer Fehlentscheidung zu kommen.

Wird als niederwertiges Codebit nun das durch den Faltungscoder hinzugefügte Redundanzbit gewählt, in dem Beispiel mit einem drei Bit langen Codewort das 3. Bit, so hat dieses Bit bei der Übertragung die größte Fehlerwahrscheinlichkeit falsch decodiert zu werden da es den geringsten Abstand zu benachbarten Symbolen aufweist. Zugleich trägt es aber auch die geringste Information, da es nur aus den anderen beiden Datenbits abgeleitet wird. Die höherwertigen Bits im Codewort sind bei der TCM, je nach gewählten Faltungscoder, oft gar nicht speziell codiert, sondern entsprechen direkt den Nutzdatenbits. Bei diesen Bits liegt durch die Symbolaufteilung (set partitioning) bereits ein wesentlich größerer euklidischer Abstand zwischen den Sendesymbolen vor und damit eine deutlich geringere Fehlerwahrscheinlichkeit bei der Decodierung.

Decoder

Trellis-Diagramm mit vier Zuständen über fünf Zeitpunkte.

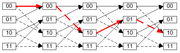
Bei der Decodierung von TCM-Signales werden die von Faltungscodes bekannten Verfahren wie der Viterbi-Algorithmus verwendet. Dargestellt werden kann der Decodierungsvorgang in einem sogenannten Trellis-Diagramm, wie es nebenstehend für einen Faltungscoder mit vier Zuständen abgebildet ist. Ein Trellis-Diagramm ist die Darstellung eines Zustandsübergangsdiagrammes, das über die Zeitachse „abgerollt“ wird. Die Übergänge von einem Zustand in den nächsten bekommen verschiedene Wahrscheinlichkeitswerte zugeordnet, wodurch in Folge sich über mehrere Zustände hinweg meist eindeutig ein einziger Pfad im Trellis herausbildet, der die geringste Summenfehlerwahrscheinlichkeit gegenüber allen anderen Pfaden aufweist. Die diesem Pfad zugeordneten Symbole werden dann vom Decoder als die am wahrscheinlichsten gesendeten Symbole angesehen.

Als Besonderheit ist bei der Decodierung der TCM zu beachten, dass durch die uncodierten, höherwertigen Datenbits sich in dem Trellis-Diagramm parallel verlaufende Zweige ergeben. (in nebenstehender Abbildung ist dieser bei TCM auftretender Umstand nicht dargestellt) Diese Mehrdeutigkeiten können durch Faltungscoder höherer Ordnung, mit mehreren Zuständen, vermieden werden.

Generell hat die Länge des Faltungscode wesentlichen Einfluss auf den Codegewinn, wobei gilt, dass je länger der Faltungscode ist, je mehr innere Zustände er umfasst, desto größer ist der damit verbundene Codegewinn. Da der Codegewinn bei der TCM auch von der verwendeten Modulation abhängt, ist in nachfolgender Tabelle nur für die Modulation 8-PSK, bei einer Bitfehlerrate (BER) von 10^-6 und in Abhängigkeit des konkreten Faltungscoders der ermittelte Codegewinn angegeben. Für andere Modulationen ergeben sich ähnliche Werte und ausführliche Tabellen finden sich dazu in unten angegebener Literatur.

Anzahl der Zustände im Faltungscoder	Codegewinn der TCM bei 8-PSK in dB
4	3
8	3,6
16	4,1
32	4,6
64	5,0
128	5,2
256	5,8
1024	6,1
4096	6,4
131072	6,9

Generell lässt sich sagen, dass Faltungscoder mit nur vier inneren Zuständen bei TCM keinen Vorteil bieten, da ein Faltungscode mit vier Zuständen für sich alleine bereits einen Codegewinn von 3,6 dB aufweist. Ab einem Faltungscode von acht Zuständen aufwärts ist allerdings die TCM als Kombination immer dem alleinigen Faltungscode im Codegewinn überlegen.

Erweiterungen realer Implementierungen

Bei realen Implementierungen der Trellis-Coded-Modulation, wie in dem ITU-T Standard V.34, kommen noch weitere Verfahren zur Verbesserung der Übertragungseigenschaften zum Einsatz. Diese Erweiterungen umfassen unter anderem folgende Punkte:

1. Einsatz von nichtlinearen Faltungscodern. Dies sind Faltungscoder, die verschiedenartige Rückkopplungen zwischen den Zustandsspeichern aufweisen. Die Auswahl verwendbarer, nichtlinearer Faltungscoder ist ungleich schwieriger als die Auswahl bei linearen, vorwärtsbasierenden Faltungscodern und in Ermangelung systematischer Konstruktionsverfahren meist nur durch umfangreiche Simulationen zu bewerkstelligen. Der Grund für den Einsatz entsprechend ausgewählter, nichtlinearer Faltungscoder besteht unter anderem darin, dass damit der Decoder die korrekte Referenzphasenlage (Drehung der komplexenen Ebene) direkt ohne Fehlerabschätzung bei der Decodierung erfassen kann und damit längere Synchronisationszeiten bzw. laufende Resynchronisationszeiten im Betrieb vermieden werden können.
2. Einsatz höherdimensionaler bzw. multidimensionaler TCM. Dabei werden die Symbole in der komplexen Ebene in einzelne Teilbereiche, so genannte Lattice, aufgeteilt, und innerhalb jeder dieser Teilbereiche eine eigene TCM durchgeführt. Damit kann unter anderem die spektrale Effizienz des gesamten Übertragungssystems gesteigert werden.

Literatur

• Todd K. Moon: Error correction coding: mathematical methods and algorithms. John Wiley & Sons, 2005, ISBN 0-471-64800-0, S. 535 bis 580. 

Weblinks

• Trellis Coded Modulation Tutorial (engl.)

Einzelnachweise

1. ↑ Gottfried Ungerböck: Channel coding with multilevel/phase signals, IEEE Trans. Inform. Theory, Volumen IT-28, Seite 55 bis 67, 1982
2. ↑ Gottfried Ungerböck: Trellis-coded modulation with redundant signal sets part I: introduction, IEEE Communications Magazine, Volumen 25-2, Seiten 5 bis 11, 1987

Technische Modulationsverfahren

Übersicht: Modulator 

Analoge Modulationsverfahren: AM | SSB | DSBSC | SSBSC | FM | PM | VM 

Digitale Modulationsverfahren: ASK | FSK | GFSK | QPSK | QAM | OFDM | DMT | TCM 

Pulsmodulationsverfahren: PWM | PAM | PFM | PPM | PCM 

Spezielle Modulationsverfahren: FHSS | DSSS 

Optische Modulationsverfahren: Allgemein | Polarisationsmodulatoren | Akustooptischer Modulator | Photoelastischer Modulator