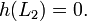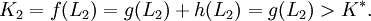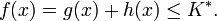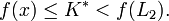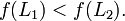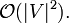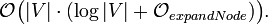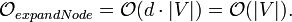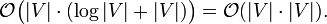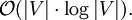A-Stern-Algorithmus

Der A*-Algorithmus („A Stern“ oder englisch „a star“) gehört zur Klasse der informierten Suchalgorithmen. Er dient in der Informatik der Berechnung eines kürzesten Pfades zwischen zwei Knoten in einem Graphen mit positiven Kantengewichten. Er wurde das erste Mal 1968 von Peter Hart, Nils Nilsson und Bertram Raphael beschrieben.

Im Gegensatz zu uninformierten Suchalgorithmen verwendet der A*-Algorithmus eine Schätzfunktion (Heuristik), um zielgerichtet zu suchen und damit die Laufzeit zu verringern. Der Algorithmus ist optimal. Das heißt, es wird immer die optimale Lösung gefunden, falls eine existiert.

Inhaltsverzeichnis

1 Idee des Algorithmus
2 Funktionsweise
3 Anwendungsgebiete
4 Beispiel
5 Heuristiken
- 5.1 Zulässige Heuristik
- 5.2 Monotone Heuristik
6 Eigenschaften
7 Verwandte Algorithmen
8 Literatur
9 Weblinks

Idee des Algorithmus

Der A*-Algorithmus untersucht immer die Knoten zuerst, die wahrscheinlich schnell zum Ziel führen. Um den vielversprechendsten Knoten zu ermitteln, wird allen bekannten Knoten $x$ jeweils ein Wert $f (x)$ zugeordnet, der angibt, wie lange der Pfad vom Start zum Ziel unter Verwendung des betrachteten Knotens im günstigsten Fall ist. Der Knoten mit dem niedrigsten $f$ Wert wird als nächstes untersucht.

$f (x) = g (x) + h (x)$

Für einen Knoten $x$ bezeichnet $g (x)$ die bisherigen Kosten vom Startknoten aus, um $x$ zu erreichen. $h (x)$ bezeichnet die geschätzten Kosten von $x$ bis zum Zielknoten. Die verwendete Heuristik darf die Kosten nie überschätzen. Für das Beispiel der Wegsuche ist die Luftlinie eine geeignete Schätzung: Die tatsächliche Strecke ist nie kürzer als die direkte Verbindung.

Funktionsweise

Die Knoten werden während der Suche in drei verschiedene Klassen eingeteilt:

unbekannte Knoten: Diese Knoten wurden während der Suche noch nicht gefunden. Zu ihnen ist noch kein Weg bekannt. Jeder Knoten (außer dem Startknoten) ist zu Beginn des Algorithmus unbekannt.
bekannte Knoten: Zu diesen Knoten ist ein (möglicherweise suboptimaler) Weg bekannt. Alle bekannten Knoten werden zusammen mit ihrem $f$ -Wert in der sogenannten Open List gespeichert. Aus dieser Liste wird immer der vielversprechendste Knoten ausgewählt und untersucht. Die Implementierung der Open List hat großen Einfluss auf die Laufzeit und wird oft als einfache Prioritätswarteschlange (z. B. binärer Heap) realisiert. Zu Beginn ist nur der Startknoten bekannt.
abschließend untersuchte Knoten: Zu diesen Knoten ist der kürzeste Weg bekannt. Die abschließend untersuchten Knoten werden in der sogenannten Closed List gespeichert, damit sie nicht mehrfach untersucht werden. Die Closed List ist zu Beginn leer.

Jeder bekannte oder abschließend besuchte Knoten enthält einen Zeiger auf seinen Vorgängerknoten. Mit Hilfe dieser Zeiger kann der Pfad bis zum Startknoten rückverfolgt werden.

Wird ein Knoten $x$ abschließend untersucht (auch expandiert oder relaxiert), so werden seine Nachfolgeknoten in die Open List eingefügt und $x$ auf die Closed List gesetzt. Die Vorgängerzeiger der Nachfolgeknoten werden auf $x$ gesetzt. Ist ein Nachfolgeknoten bereits auf der Closed List, so wird er nicht erneut in die Open List eingefügt und auch sein Vorgängerzeiger nicht geändert. Ist ein Nachfolgeknoten bereits auf der Open List, so wird der Knoten nur aktualisiert ( $f$ -Wert und Vorgängerzeiger), wenn der neue Weg dorthin kürzer ist als der bisherige.

Falls der Zielknoten abschließend untersucht wird, terminiert der Algorithmus. Der gefundene Weg wird mit Hilfe der Vorgängerzeiger rekonstruiert und ausgegeben. Falls die Open List leer ist, gibt es keine Knoten mehr, die untersucht werden könnten. In diesem Fall terminiert der Algorithmus, da es keine Lösung gibt.

Bedingt durch die Vorgängerzeiger wird der gefundene Weg vom Ziel ausgehend rückwärts bis zum Start ausgegeben. Um den Weg in der richtigen Reihenfolge zu erhalten kann z. B. vor der Wegsuche Start und Ziel vertauscht werden. Somit wird vom eigentlichen Ziel zum Start gesucht und die Wegausgabe beginnt beim ursprünglichen Startknoten.

Anmerkung: Die Closed List kann auch indirekt implementiert werden. Dazu speichern auch die abschließend untersuchten Knoten ihren

f

-Wert. Wird nun ein abschließend untersuchter Knoten erneut gefunden, ist sein alter

f

-Wert geringer als der neue, da der kürzeste Weg zu diesem Knoten bereits gefunden wurde. Der Knoten wird also nicht erneut in die Open List eingefügt.

Wird keine Closed List benutzt, muss anderweitig sicher gestellt werden, dass Knoten nicht mehrfach untersucht werden. Ansonsten wird die worst-case Laufzeit schlechter als quadratisch. Außerdem terminiert der Algorithmus nicht mehr, wenn es keine Lösung gibt. Die Knoten werden dann unendlich oft untersucht, da die Open List nie leer wird.

program a-star
    // Initialisierung der Open List, die Closed List ist noch leer
    // (die Priorität bzw. der f Wert des Startknotens ist unerheblich)
    openlist.enqueue(startknoten, 0)
    // diese Schleife wird durchlaufen bis entweder
    // - die optimale Lösung gefunden wurde oder
    // - feststeht, dass keine Lösung existiert
    repeat
        // Knoten mit dem geringsten f Wert aus der Open List entfernen
        currentNode := openlist.removeMin()
        // Nachfolgeknoten auf die Open List setzen
        expandNode(currentNode)
        // wurde das Ziel gefunden?
        if currentNode == zielknoten then
            return PathFound
        // der aktuelle Knoten ist nun abschließend untersucht
        closedlist.add(currentNode)
    until openlist.isEmpty()
    // die Open List ist leer, es existiert kein Pfad zum Ziel
    return NoPathFound
end

// überprüft alle Nachfolgeknoten und fügt sie der Open List hinzu, wenn entweder
// - der Nachfolgeknoten zum ersten Mal gefunden wird oder
// - ein besserer Weg zu diesem Knoten gefunden wird
function expandNode(currentNode)
    foreach successor of currentNode
        // wenn der Nachfolgeknoten bereits auf der Closed List ist - tue nichts
        if closedlist.contains(successor) then
            continue
        // f Wert für den neuen Weg berechnen: g Wert des Vorgängers plus die Kosten der
        // gerade benutzten Kante plus die geschätzten Kosten von Nachfolger bis Ziel
        f := g(currentNode) + c(currentNode, successor) + h(successor)
        // wenn der Nachfolgeknoten bereits auf der Open List ist,
        // aber der neue Weg länger ist als der alte - tue nichts
        if openlist.contains(successor) and f > openlist.find(successor).f then
            continue
        // Vorgängerzeiger setzen
        successor.predecessor := currentNode
        // f Wert des Knotens in der Open List aktualisieren
        // bzw. Knoten mit f Wert in die Open List einfügen
        if openlist.contains(successor) then
            openlist.decreaseKey(successor, f)
        else
            openlist.enqueue(successor, f)
    end
end

Anwendungsgebiete

Der A*-Algorithmus findet allgemein einen optimalen Pfad zwischen zwei Knoten in einem Graphen. Optimal kann dabei am kürzesten, am schnellsten oder auch am einfachsten bedeuten, je nach Art der Gewichtungsfunktion, die den Kanten ihre Länge zuordnet. Theoretisch kann der Algorithmus alle Probleme lösen, die durch einen Graphen dargestellt werden können und bei denen eine Schätzung über die Restkosten bis zum Ziel gemacht werden kann. Zu den Beschränkungen von A* siehe den Abschnitt Nachteile.

A* wird oft zur Wegsuche bei Routenplanern oder in Computerspielen benutzt. Als Heuristik wird dabei meist der Abstand zum Ziel verwendet. Weitere Anwendungsgebiete sind Spiele wie das 15-Puzzle oder das Damenproblem, bei dem ein vorgegebener Zielzustand erreicht werden soll. Als Heuristik kann dabei die Anzahl der falsch platzierten Steine verwendet werden.

Beispiel

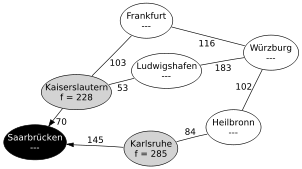
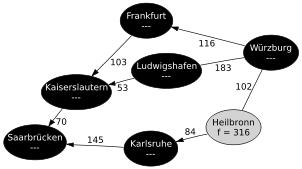
Landkarte als Graph. (Angaben in Kilometern)

Im Beispiel soll der kürzeste Weg von Saarbrücken nach Würzburg gefunden werden. Das Diagramm zeigt eine kleine Auswahl an Städten und Wegen. Die Kantenbeschriftung entspricht den Kosten (hier: Entfernung in Kilometern), um von einer Stadt zur nächsten zu kommen. Jeder Knoten enthält die geschätzte Entfernung zum Zielknoten (Wert der $h$ Funktion). Als Heuristik wird hier die Luftlinie verwendet.

Auf den Schritt-für-Schritt Bildern zeigt die Farbe eines Knotens seinen Status an:

weiß: noch nicht gefunden
grau: gefunden, befindet sich auf der Open List
schwarz: untersucht, befindet sich auf der Closed List

Sobald ein Knoten erreicht wurde, zeigt eine Kante auf den Vorgängerknoten. Für alle Knoten auf der Open List ist der $f$ Wert angegeben.

Schritt 1: Der Startknoten Saarbrücken wurde erkundet.

Schritt 1: Es werden alle Nachfolgeknoten vom Startknoten Saarbrücken betrachtet:

Kaiserslautern wird mit $f K L = g (S B) + c (S B, K L) + h (K L) = 0 + 70 + 158 = 228$ in die Open List eingefügt. (Die Kosten, um von Saarbrücken nach Saarbrücken zu kommen sind 0, die Kosten der Kante Saarbrücken–Kaiserslautern betragen 70, und die geschätzten Restkosten Kaiserslautern–Würzburg liegen bei 158. Dabei bezeichnet $c (k, k')$ die Kosten der Kante zwischen den Knoten $k$ und $k'$ .)
Karlsruhe wird mit $f K A = g (S B) + c (S B, K A) + h (K A) = 0 + 145 + 140 = 285$ in die Open List eingefügt.

Saarbrücken wird in beiden Knoten als Vorgängerknoten eingetragen. Der Knoten Saarbrücken ist nun abschließend betrachtet und wird auf die Closed List gesetzt. (Intuitiv: Es ist sinnlos, erst eine Weile umherzufahren, dabei wieder am Start anzukommen, dann irgendwann anzukommen und zu behaupten, das wäre der optimale Weg.)

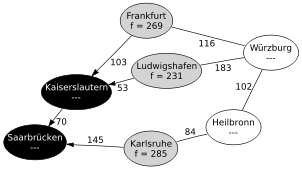
Schritt 2: Kaiserslautern wurde erkundet.

Schritt 2: Die Open List enthält nun zwei Punkte. Da Kaiserslautern den geringeren $f$ Wert hat, wird nun Kaiserslautern als nächstes untersucht und seine Nachfolgeknoten betrachtet. (Der Weg über Kaiserslautern ist mindestens 228 km lang, der über Karlsruhe mindestens 285 km. Daher ist es am geschicktesten, zuerst Kaiserslautern genauer zu überprüfen.)

Saarbrücken ist bereits auf der Closed List und wird nicht weiter betrachtet.
Frankfurt wird mit $f F = g (K L) + c (K L, F) + h (F) = 70 + 103 + 96 = 269$ in die Open List eingefügt. Die Kosten bis Frankfurt berechnen sich aus den Kosten bis Kaiserslautern plus die Kosten der zuletzt genutzten Kante (Kaiserslautern–Frankfurt). Kaiserslautern wird als Vorgängerknoten gespeichert.
Ludwigshafen wird mit $f L U = g (K L) + c (K L, L U) + h (L U) = 70 + 53 + 108 = 231$ in die Open List eingefügt. Kaiserslautern wird als Vorgängerknoten gespeichert.

Kaiserslautern wird auf die Closed List gesetzt.

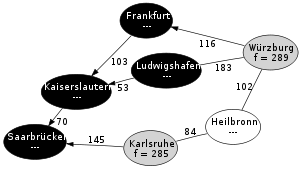
Schritt 3: Ludwigshafen wurde erkundet.

Schritt 3: Der Knoten mit dem geringsten $f$ Wert ist Ludwigshafen. (Die tatsächlichen Kosten von Ludwigshafen nach Würzburg weichen deutlich von der Schätzung ab, da in diesem Beispiel nur Autobahnen verwendet werden sollen.)

Kaiserslautern ist bereits auf der Closed List und wird nicht weiter betrachtet.
Der Zielknoten Würzburg wird gefunden, aber noch nicht als Lösung ausgegeben, sondern zunächst in die Open List eingefügt. Ludwigshafen wird als Vorgängerknoten gespeichert.

Ludwigshafen wird auf die Closed List gesetzt.

Hier wird ein wichtiger Unterschied zwischen „Knoten befindet sich auf der Open List“ und „Knoten befindet sich auf der Closed List“ deutlich: Solange ein Knoten nicht abschließend betrachtet wurde ist der Pfad zu diesem Knoten nur vorläufig. Eventuell gibt es noch einen besseren Pfad! Knoten auf der Closed List hingegen sind abschließend betrachtet. Der kürzeste Pfad dorthin ist bekannt.

Schritt 4: Frankfurt wurde erkundet.

Schritt 4: Frankfurt wird erkundet. Als einziger Nachfolgeknoten, der sich noch nicht auf der Closed List befindet, wird Würzburg gefunden. Als $f$ Wert wird 289 berechnet, was geringer als der bisherige $f$ Wert für Würzburg ist. Dies bedeutet, dass der Weg über Frankfurt kürzer ist, als der zuerst gefundene Weg über Ludwigshafen. Daher wird der $f$ Wert von Würzburg geändert. Außerdem wird als Vorgängerknoten nun Frankfurt gespeichert.

Frankfurt wird auf die Closed List gesetzt.

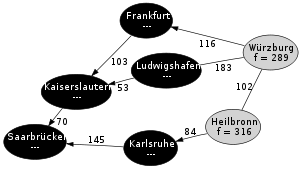
Schritt 5: Karlsruhe wurde erkundet.

Schritt 5: Da Karlsruhe nun den kleinsten $f$ Wert hat, wird dieser Knoten als nächstes untersucht. Heilbronn wird in die Open List eingefügt und Karlsruhe auf die Closed List gesetzt.

Schritt 6: Der Zielknoten Würzburg wurde erkundet.

Schritt 6: Jetzt hat Würzburg den geringsten $f$ Wert und wird untersucht: Das Ziel ist gefunden und der kürzeste Weg ist: Saarbrücken–Kaiserslautern–Frankfurt–Würzburg

Dieses Beispiel dient lediglich dem Verständnis der Funktionsweise des Algorithmus. Die Besonderheit des zielgerichteten Suchens wird hier nicht deutlich, da alle Knoten im Bereich der direkten Verbindungslinie Saarbrücken–Würzburg liegen. Unter Weblinks finden sich Java-Applets, die das zielgerichtete Suchen besser darstellen.

Heuristiken

Es gibt zwei Arten von Heuristiken für den A*-Algorithmus: Zulässige und monotone Heuristiken. Jede monotone Heuristik ist auch zulässig. Monotonie ist also eine stärkere Eigenschaft als die der Zulässigkeit. Im Allgemeinen werden monotone Heuristiken verwendet. Die Heuristik zur Abschätzung der Entfernung zweier Städte – die Luftlinie – ist zum Beispiel monoton.

Zulässige aber nicht monotone Heuristik. A*-Algorithmus mit Closed List nach dem dritten Schritt. Jeder Knoten wurde schon einmal gefunden und zeigt auf seinen Vorgängerknoten.

Zulässige Heuristik

Eine Heuristik ist zulässig, wenn die Kosten nie überschätzt werden. Das heißt, die geschätzten Kosten müssen stets im Intervall $[0; k]$ liegen, wenn $k$ die tatsächlichen Kosten bezeichnet. Ist die verwendete Heuristik nur zulässig, aber nicht monoton, dann ist zu einem expandierten Knoten nicht notwendigerweise der kürzeste Weg bekannt. Daher muss es möglich sein, einen Knoten mehrfach zu expandieren. Es darf also keine Closed List benutzt werden.

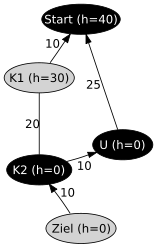
Im Diagramm rechts ist ein Beispielgraph und eine zulässige (aber nicht monotone) Heuristik dargestellt. Der beste Weg vom Start zum Ziel hat Kosten 40 und führt über die Knoten K1 und K2. Der Weg über den Umwegknoten U hat Kosten 45. Beim Startknoten schätzt die Heuristik Kosten von 40 und beim Knoten K1 Kosten von 30, was jeweils den tatsächlichen Kosten entspricht. Bei den Knoten K2, U und Ziel werden Kosten von 0 geschätzt. Da eine Heuristik nicht überschätzen darf, werden für einen Zielknoten immer Kosten von 0 geschätzt.

Beispiel mit Closed List

Im ersten Schritt wird der Startknoten expandiert. Die beiden Nachfolgeknoten K1 und U werden gefunden und mit den Werten $f K 1 = 10 + 30 = 40$ und $f U = 25 + 0 = 25$ in die Open List eingetragen.
Im zweiten Schritt wird der Knoten U expandiert, da sein $f$ Wert am niedrigsten ist. Der Nachfolgeknoten K2 wird gefunden und mit dem Wert $f K 2 = 35 + 0 = 35$ in die Open List eingetragen.
Im dritten Schritt besteht die Open List aus den Knoten K2 mit $f K 2 = 35$ und dem Knoten K1 mit $f K 1 = 40$ . Also wird der Knoten K2 expandiert. Die beiden Nachfolgeknoten K1 und Ziel werden gefunden. Der neue Wert $f K 1' = 55 + 30 = 85$ ist größer als der alte Wert. Daher wird der $f$ Wert für den Knoten K1 in der Open List nicht aktualisiert. Der Zielknoten wird mit $f Z i e l = 45 + 0 = 45$ in die Open List eingefügt.
Im vierten Schritt befinden sich die Knoten K1 mit $f K 1 = 40$ und Ziel mit $f Z i e l = 45$ in der Open List. Die Expansion von K1 erzeugt keine Nachfolgeknoten, da sich sowohl Start als auch K2 bereits auf der Closed List befinden. Die Verwendung der Closed List verhindert hier, dass die optimale Lösung gefunden wird.
Im fünften Schritt wird der einzige Knoten auf der Open List expandiert: der Zielknoten. Die gefundene Lösung ist also Start–U–K2–Ziel und mit Kosten 45 nicht optimal.

Beispiel ohne Closed List

Im ersten Schritt wird der Startknoten expandiert. Die beiden Nachfolgeknoten K1 und U werden gefunden und mit den Werten $f K 1 = 10 + 30 = 40$ und $f U = 25 + 0 = 25$ in die Open List eingetragen.
Im zweiten Schritt wird der Knoten U mit $f U = 25$ expandiert. Die Nachfolgeknoten K2 und Start werden gefunden und mit den Werten $f K 2 = 35 + 0 = 35$ und $f S t a r t = 50 + 40 = 90$ in die Open List eingetragen.
Im dritten Schritt wird der Knoten K2 expandiert. Die Nachfolgeknoten K1 ( $f K 1 = 55 + 30 = 85$ ), U ( $f U = 45 + 0 = 45$ ) und Ziel ( $f Z i e l = 45 + 0 = 45$ ) werden gefunden.
Im vierten Schritt werden die Nachfolgeknoten von K1 ( $f K 1 = 40$ ) in die Open List eingefügt: Start mit $f S t a r t = 20 + 40 = 60$ und K2 mit $f K 2 = 30 + 0 = 30$ .
Im fünften Schritt wird K2 zum zweiten Mal expandiert, jetzt mit $f K 2 = 30$ . Die Knoten K1 ( $f K 1 = 50 + 30 = 80$ ), U ( $f U = 40 + 0 = 40$ ) und Ziel ( $f Z i e l = 40 + 0 = 40$ ) werden gefunden.
Im sechsten Schritt befinden sich 8 Knoten auf der Open List ( $f Z i e l = 40$ , $f U = 40$ , $f U = 45$ , $f Z i e l = 45$ , $f S t a r t = 60$ , $f K 1 = 80$ , $f K 1 = 85$ , $f S t a r t = 90$ ). Die beiden Knoten U und Ziel haben jeweils mit 40 den niedrigsten $f$ Wert. Welcher Knoten expandiert wird hängt vom Zufall (genauer: Implementierungsdetails) ab. Auf die gefundene Lösung hat dies jedoch keinen Einfluss. Sobald der Zielknoten expandiert wird (entweder in diesem oder im nächsten Schritt) ist mit dem Pfad Start–K1–K2–Ziel die optimale Lösung gefunden.

Monotone Heuristik

Damit eine Heuristik monoton (oder konsistent) ist, muss sie zwei Bedingungen erfüllen:

Die Kosten dürfen nie überschätzt werden (Bedingung für eine zulässige Heuristik).
Für jeden Knoten $k$ und jeden Nachfolgeknoten $k'$ von $k$ muss gelten 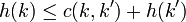$h(k) \le c(k, k') + h(k')$ . Hierbei bezeichnet $c (k, k')$ die tatsächlichen Kosten, um von $k$ nach $k'$ zu kommen.

Die zweite Bedingung ist eine Form der Dreiecksungleichung: Die geschätzten Kosten von einem Knoten $k$ dürfen nicht größer sein als die tatsächlichen Kosten zu einem Nachbarknoten $k'$ plus die geschätzten Kosten dieses Knotens.

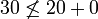Die zulässige Heuristik aus dem Beispiel verletzt diese Bedingung: Die Kosten von Knoten K1 werden mit 30 geschätzt. Bewegt man sich nun 20 in Richtung des Ziels zu Knoten K2 werden plötzlich keine Kosten mehr geschätzt. Hier gilt $30 \not\le 20 + 0$ .

Eine monotone Heuristik ist z. B. der euklidische Abstand.

Eigenschaften

Der A*-Algorithmus ist

vollständig: Falls eine Lösung existiert, wird sie gefunden.
optimal: Es wird immer die optimale Lösung gefunden. Existieren mehrere optimale Lösungen, wird eine davon gefunden (abhängig von Implementierungsdetails).
optimal effizient: Es gibt keinen anderen Algorithmus, der die Lösung unter Verwendung der gleichen Heuristik schneller findet. (genauer: A* expandiert eine minimale Anzahl an Knoten.)

Optimalität

Der A*-Algorithmus ist optimal, falls eine monotone Heuristik verwendet wird. Wenn keine Closed List verwendet wird, bleibt die Optimalität auch bei einer zulässigen Heuristik erhalten. Im Folgenden wird die Optimalität unter Verwendung einer monotonen Heuristik bewiesen.

Behauptung: Der A*-Algorithmus findet immer eine optimale Lösung.

Beweis: Sei $L 1$ eine optimale Lösung mit Kosten $K *$ und $L 2$ eine suboptimale Lösung. Da die Heuristik die Kosten bis zum Ziel nie überschätzt, gilt für jeden Zielknoten und insbesondere für $L 2$ :

$h(L_2)\!\, = 0.$

Da $L 2$ eine suboptimale Lösung ist, gilt für die Kosten $K 2$ :

$K_2\!\, = f(L_2) = g(L_2) + h(L_2) = g(L_2) &amp;gt; K^*.$

Die Heuristik schätzt die tatsächlichen Kosten oder unterschätzt sie. Also gilt für einen beliebigen Knoten $x$ auf dem kürzesten Pfad zur optimalen Lösung $L 1$ :

$f(x) = g(x) + h(x) \le K^*.$

Damit gilt:

$f(x) \le K^* &amp;lt; f(L_2).$

und insbesondere:

$f(L_1)\!\, &amp;lt; f(L_2).$

Dies bedeutet, dass der A*-Algorithmus die suboptimale Lösung $L 2$ nicht ausgibt, solange eine bessere Lösung existiert. Es wird also zuerst die optimale Lösung $L 1$ gefunden.

Zeitkomplexität

Die hier beschriebene Zeitkomplexität (oder asymptotische Laufzeit) hat nur geringe Bedeutung, da die Stärke des A*-Algorithmus im zielgerichteten Suchen liegt und im Vergleich zur Gesamtanzahl der Knoten meist nur ein kleiner Teil davon untersucht wird. Bei Labyrinthen ist dies jedoch oft nicht möglich und die tatsächliche Laufzeit nähert sich der angegebenen worst-case Laufzeit an. Die Zeitkomplexität wird hier nur unter Verwendung von vereinfachenden Annahmen abgeschätzt. Sie hängt sehr stark von zwei Faktoren ab:

Genauigkeit der verwendeten Heuristik: Ist die Heuristik nicht monoton, wird die Laufzeit exponentiell, da Knoten mehrfach expandiert werden. Je genauer die Kostenabschätzung ist, desto weniger Knoten werden untersucht.
Implementierung der Open und Closed List: Die kostenintensiven Operationen im A*-Algorithmus sind die Methoden, um Elemente in die Listen einzufügen und zu entfernen, sowie Elemente in der Open List zu ändern. Diese müssen von den verwendeten Datenstrukturen effizient unterstützt werden, um eine kurze Laufzeit zu ermöglichen.

Im Folgenden wird die Menge der Knoten des zu Grunde liegenden Graphen mit $V$ bezeichnet. Es wird angenommen, dass alle Knoten und Kanten im Voraus bekannt sind. (Dies ist bei einer Wegsuche meist der Fall.) Die verwendete Heuristik ist monoton. Die Open List wird als binärer Heap implementiert, die Closed List als Array. (Jeder Knoten besitzt ein Flag, ob er auf der Liste ist oder nicht.) Der A*-Algorithmus hat damit eine quadratische worst-case Laufzeit:

$\mathcal{O}(\vert V \vert^2).$

Diese Laufzeit ergibt sich wie folgt: Die Hauptschleife des Algorithmus wird für jeden Knoten maximal einmal ausgeführt. Die Funktionen openlist.removeMin, expandNode und closedlist.add werden also maximal $V$ -mal aufgerufen. openlist.removeMin enthält maximal $V$ Knoten und benötigt bei einem binären Heap logarithmische Laufzeit. closedlist.add benötigt bei einem Array nur konstante Laufzeit. Dadurch ergibt sich eine vorläufige Laufzeit von:

$\mathcal{O}\big(\vert V \vert \cdot (\log \vert V \vert + \mathcal{O}_{expandNode})\big).$

Die Laufzeit von expandNode setzt sich zusammen aus: closedlist.contains hat konstante Laufzeit. openlist.contains hat ebenfalls konstante Laufzeit, wenn man zu jedem Knoten auch ein Open List Flag speichert. Der Aufruf von openlist.find kann entfallen, wenn jeder Knoten auch seinen $f$ Wert speichert. Es wird entweder openlist.decreaseKey (benötigt lineare Laufzeit, um das entsprechende Element zu finden) oder openlist.enqueue (benötigt logarithmische Laufzeit) aufgerufen. Dabei wird die logarithmische von der linearen Laufzeit dominiert. Ein Schleifendurchlauf innerhalb von expandNode benötigt somit lineare Laufzeit.

Alle Funktionen werden für jeden Nachfolgeknoten aufgerufen. Es wird angenommen, dass jeder Knoten nur maximal $d$ ausgehende Kanten hat. Die Anzahl der Schleifendurchläufe innerhalb von expandNode ist somit konstant und kann bei der asymptotischen Laufzeitbetrachtung vernachlässigt werden. Diese Annahme gilt nicht für Graphen, in denen jeder Knoten mit fast jedem anderen Knoten verbunden ist.

$\mathcal{O}_{expandNode} = \mathcal{O}(d \cdot \vert V \vert) = \mathcal{O}(\vert V \vert).$

Die Gesamtlaufzeit ergibt sich als:

$\mathcal{O}\big(\vert V \vert \cdot (\log \vert V \vert + \vert V \vert)\big) = \mathcal{O}(\vert V \vert \cdot \vert V \vert).$

Optimierungspotential in Bezug auf die worst-case Laufzeit besteht vor allem bei openlist.decreaseKey. Das teure Suchen im Heap entfällt, wenn jeder Knoten die Position seines entsprechenden Eintrages im Heap speichert. Damit würde sich die Laufzeit von decreaseKey zu logarithmisch und die Gesamtlaufzeit zu linear-logarithmisch reduzieren:

$\mathcal{O}(\vert V \vert \cdot \log \vert V \vert).$

Nachteile

Der begrenzende Faktor bei A* ist oft nicht die Rechenzeit, sondern der Speicherplatz. Da alle bekannten Knoten im Speicher gehalten werden (Open und Closed List), ist A* für viele Probleme nicht geeignet. Schon beim einfachen 15-Puzzle hat der komplette Graph bereits $16! = 20.922.789.888.000$ Knoten. Bei einem entsprechend langen Lösungsweg reicht der verfügbare Speicher nicht aus und A* kann keine Lösung finden. Im Abschnitt Verwandte Algorithmen finden sich ähnliche Algorithmen, die versuchen, den Speicherplatzverbrauch zu beschränken.

Literatur

Stuart Russell, Peter Norvig: Künstliche Intelligenz – Ein moderner Ansatz, 2004, Prentice Hall, ISBN 3-8273-7089-2
P. E. Hart, N. J. Nilsson, B. Raphael: A Formal Basis for the Heuristic Determination of Minimum Cost Paths, IEEE Transactions on Systems Science and Cybernetics SSC4 (2), pp. 100–107, 1968.
P. E. Hart, N. J. Nilsson, B. Raphael: Correction to „A Formal Basis for the Heuristic Determination of Minimum Cost Paths“, SIGART Newsletter, 37, pp. 28–29, 1972.
Anthony Stentz: Optimal and Efficient Path Planning for Partially-Known Environments, Original D* paper, ICRA International Conference on Robotics and Automation, 1994.

Weblinks

Wikimedia Foundation.

Игры ⚽ Поможем решить контрольную работу

Schlagen Sie auch in anderen Wörterbüchern nach: