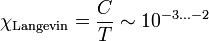Van Vleck-Paramagnetismus

Paramagnetismus ist eine Ausprägungsform von Magnetismus in Materie. Ein Paramagnet magnetisiert sich in einem externen Magnetfeld so, dass er das Magnetfeld in seinem Innern verstärkt. Die Magnetisierung ist proportional zur magnetischen Feldstärke; der Faktor wird durch die magnetische Suszeptibilität bestimmt. Paramagnetismus tritt in allen Materialien auf, deren Atome bzw. Moleküle ein magnetisches Moment besitzen. In der Physik werden alle Materialien mit positiver magnetischer Suszeptibilität und ohne magnetische Ordnung als paramagnetisch klassifiziert.

Ursprung

Illustrationen einer paramagnetischen Probe ohne äußeres Magnetfeld, ...

... in einem schwachen Magnetfeld ...

... und in einem starken Magnetfeld.

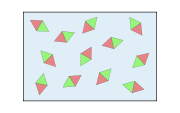
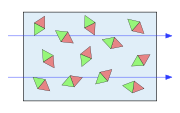
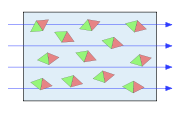
Modellhaft kann man sich eine paramagnetische Probe aus lauter kleinen Stabmagneten aufgebaut vorstellen, die sich zwar drehen, aber nicht verrutschen können. Bringt man die Probe in ein Magnetfeld, so werden sich die Stabmagnete bevorzugt in Richtung der magnetischen Feldlinien ausrichten. Ein wichtiges Merkmal dabei ist, dass die Stabmagnete einander nicht beeinflussen – sie richten sich alle unabhängig voneinander aus. Die Temperatur bewirkt eine ständige Neuorientierung der Stabmagnete, was bedeutet, dass eine zufällige Anordnung viel wahrscheinlicher als eine geordnete ist. Daher braucht man also umso stärkere Magnetfelder, je stärker man die Magnete ausrichten möchte.

Physikalisch ausgedrückt: Ursache eines paramagnetischen Verhaltens liegt in der Ausrichtung der mikroskopischen magnetischen Momente eines Stoffes in einem Magnetfeld. Die einzelnen magnetischen Momente sind dabei voneinander unabhängig. Im Unterschied zu Ferromagneten wird eine solche Ausrichtung nach Abschalten des Magnetfeldes durch thermische Fluktuationen sofort wieder zerstört. Die Magnetisierung M des Stoffes ist proportional zum angelegten Magnetfeld H

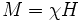$\left.M=\chi H\right.$ mit $\left.\chi>0\right.$.

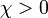Je größer dabei die magnetische Suszeptibilität χ des Stoffes ist, desto leichter lässt sich dieser demnach magnetisieren. Die Suszeptibilität ist also ein Maß für die Stärke des Paramagnetismus. Wegen des einfachen Zusammenhangs der Suszeptibilität mit der relativen magnetischen Permeabilität μ_r = χ + 1 wird auch häufig letztere als Maß genommen.

Häufig kann man lesen, dass eine sehr große Suszeptibilität bedeutet, eine Probe sei ferromagnetisch. Diese Aussage ist so nicht ganz richtig. Zwar ist die Suszeptibilität von Ferromagneten in vielen Fällen sehr groß, jedoch liegt die Ursache in der besagten Kopplung. Ferromagneten zeigen auch nach Abschalten des Magnetfeldes noch eine Magnetisierung, die sogenannte Remanenz, während bei Paramagneten, wie bereits gesagt, die Magnetisierung nach Abschalten des Feldes wieder verschwindet.

Arten

Eine klassische Betrachtung liefert keine Erklärung für das Vorhandensein der oben besprochenen magnetischen Momente. Diese lassen sich jedoch quantenmechanisch verstehen. Die für den Magnetismus wichtige Aussage dabei ist, dass der Gesamtdrehimpuls 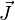$\vec J$ eines atomaren Zustandes immer mit einem magnetischen Moment 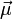$\vec \mu$ verknüpft ist

$\vec \mu=-g\mu_\mathrm{B}\vec J/{\hbar}$.

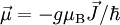Dabei ist g der Landé-Faktor und μ_B das Bohrsche Magneton. Der Gesamtdrehimpuls ergibt sich dabei aus drei Komponenten:

1. Spin und
2. Bahndrehimpuls der Elektronen sowie
3. Kernspin der Nukleonen.

Das zum Kernspin gehörende magnetische Moment ist – wegen der bedeutend größeren Masse der Nukleonen – allerdings zu schwach, um einen nennenswerten Beitrag zur Suszeptibilität liefern zu können. Daher wird dieser im Folgenden nicht weiter beachtet. Es sei aber darauf hingewiesen, dass das magnetische Moment des Kernes durchaus messbar ist, was in der Medizin bei der Magnetresonanztomografie (MRT) genutzt wird (daher wird das Verfahren auch Kernspintomografie genannt).

Die wesentlichen Beiträge zur Suszeptibilität rühren aus verschiedenen Quellen, die weiter unten aufgeführt werden. Da es jedoch immer auch diamagnetische Beiträge zur Suszeptibilität gibt, entscheidet erst eine Addition aller Beiträge, ob ein Stoff letztlich paramagnetisch ist. Tritt allerdings Langevin-Paramagnetismus (s.u.) auf, so ist dessen Beitrag üblicherweise dominant.

Magnetische Momente von Atomen im Grundzustand (Langevin-Paramagnetismus)

Der Gesamtdrehimpuls eines Atomes im Grundzustand lässt sich theoretisch über die sogenannten Hundschen Regeln bestimmen. Wichtigste Essenz daraus ist, dass sich der Gesamtdrehimpuls

1. einer abgeschlossenen Schale und
2. einer bis auf ein Elektron halb gefüllten Schale

immer zu Null addiert. In allen anderen Fällen besitzt das Atom also ein magnetisches Moment.

Die Temperaturabhängigkeit dieses Beitrags wird durch das Curiesche Gesetz

$\chi_\mathrm{Langevin}=\frac{C}{T} \sim 10 ^{-3\ldots-2}$

beschrieben, dabei ist C die Curie-Konstante (eine Materialkonstante).

Eine genauere Analyse des Langevin-Paramagnetismus geschieht mit Hilfe der Langevin- und der Brillouin-Funktion.

Magnetische Momente der Leitungselektronen (Pauli-Paramagnetismus)

Elektronen können sich praktisch frei in Metallen bewegen. Jedes Elektron besitzt ein magnetisches Moment – man erwartet also einen Curie-ähnlichen Beitrag zur Suszeptibilität. Es haben jedoch nur die angeregten Leitungselektronen wegen des Pauli-Prinzips die Freiheit, ihren Spin im Magnetfeld auszurichten. Deren Anzahl ist proportional zu T / T_F (T_F ist die Fermitemperatur, eine weitere Materialkonstante):

$\chi_\mathrm{Pauli}\sim\frac{C}{T}\cdot\frac{T}{T_\mathrm{F}}=\frac{C}{T_\mathrm{F}} \sim 10 ^{-6..-5}$.

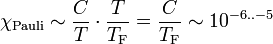Eine genaue Betrachtung zeigt allerdings, dass es eine Abhängigkeit von der Stärke des externen Magnetfeldes gibt.

Magnetische Momente von Atomen in angeregten Zuständen (Van Vleck-Paramagnetismus)

Auch wenn der Gesamtdrehimpuls eines Atomes in seinem Grundzustand Null ist, so muss das nicht für angeregte Zustände gelten. Bei einer endlichen Temperatur sind immer einige Atome in einem angeregten Zustand, daher kommt dieser Beitrag bei allen Stoffen vor. Von nennenswerter Größe ist er allerdings nur in Molekülkristallen; dort kann er den Langevin-Paramagnetismus sogar an Stärke übertreffen. Die Größe dieses Beitrages zu berechnen ist aber gerade für Moleküle recht aufwändig.

Vergleich der Größenordnungen

$\chi^{\text{van Vleck}} \approx \chi^{\text{Pauli}} \approx \chi^{\text{Larmor}} \approx 10 ^{-6\ldots-5} \ll \chi^{\text{Langevin}} \approx 10 ^{-3\ldots-2}$

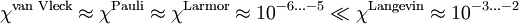
Superparamagnetismus

Die magnetischen Eigenschaften von gekörnten ferromagnetischen Festkörpern sind abhängig von der Korngröße. Bei Verkleinerung der Korngröße nimmt die Anzahl der magnetischen Bezirke (Weiss-Bezirk) pro Korn ab. Unterhalb einer kritischen Größe ist es energetisch ungünstig, mehrere dieser Bereiche auszubilden. Es existiert also nur noch ein Weiss-Bezirk pro Korn, d. h. alle atomaren magnetischen Momente eines Korns sind parallel zueinander angeordnet. Unterhalb einer weiteren kritischen Größe ist bei endlichen Temperaturen eine stabile Ausrichtung des magnetischen Gesamtmoments nicht mehr möglich, da die zur Ummagnetisierung benötigte Energie kleiner als die thermische Energie wird. Der Festkörper als Ganzes verhält sich nun paramagnetisch mit der Besonderheit, dass die magnetischen Momente nicht einzeln, sondern in Blöcken auf externe Magnetfelder reagieren. Diese besondere Form des Paramagnetismus wird als Superparamagnetismus bezeichnet.

Beispiele

Alkalimetalle

Die Elektronenhülle der Alkalimetalle besteht aus einer Edelgaskonfiguration und einem zusätzlichen s-Elektron. Nach den Hundschen Regeln besitzen die Atome im Grundzustand also ein magnetisches Moment. Dies ist der erste Fall (s.o.), der einen starken Beitrag zur Suszeptibilität liefert. Die Alkalimetalle sind demnach paramagnetisch.

Erdalkalimetalle

Im Gegensatz zu den Alkalimetallen besitzen die Erdalkalimetalle zwei s-Elektronen und damit eine abgeschlossene Unterschale. Jedoch gehören sie zu den Metallen und fallen damit in den zweiten Fall. Mit Ausnahme von Beryllium überwiegt dieser Beitrag den diamagnetischen, womit die Erdalkalimetalle schwach paramagnetisch sind.

Seltene Erden

Die Seltenen Erden gehören zu den technisch wichtigsten Materialien für Legierungen in Permanentmagneten. Die Ursache liegt darin, dass die entscheidende nicht vollständig besetzte Schale im Inneren der Elektronenhülle liegt (f-Elektronen) und somit keinen Einfluss auf die chemischen Eigenschaften der Atome hat. Fast alle seltene Erden sind daher paramagnetisch (nach dem ersten Fall), jedoch variiert dessen Stärke. Das macht sie zu idealen Kandidaten in Legierungen mit ferromagnetischen Materialien, wodurch sehr starke Permanentmagnete hergestellt werden können.

Moleküle

Da Moleküle häufig eine abgeschlossene Elektronenkonfigation haben und keine Metalle sind, zeigen sie nur einen Beitrag nach dem dritten Fall. Einige Beispiele für paramagnetische Substanzen sind:

• Stickstoffdioxid
• Sauerstoff

Magnetit

Magnetit (Fe₃O₄) zeigt normalerweise ferrimagnetisches Verhalten (Ferrimagnetismus).
Bei Teilchengrößen, welche kleiner als 20 bis 30nm sind, zeigt sich bei Raumtemperatur superparamagnetisches Verhalten. Bei Anwesenheit eines äußeren magnetischen Feldes richten sich alle Teilchen in Richtung dieses Feldes aus. Nach Entfernen des äußeren Feldes ist die thermische Energie groß genug, sodass die gemeinsame Ausrichtung der Teilchen relaxiert und die Magnetisierung wieder gegen Null geht.

Weiterführende Literatur

Siehe auch

• Elektronenspinresonanz
• Magnetochemie
• Faraday-Waage
• Ferrofluid
• Zeeman-Effekt
• Stern-Gerlach-Versuch
• Pyromagnetismus
• Diamagnetismus
• Ferromagnetismus

Literatur

• Dieter Meschede: Gerthsen Physik. 18.Auflage. Springer-Verlag, Berlin 1995, S. 390f., ISBN 3-540-59278-4 – Kurzer Überblick über den Paramagnetismus.
• Neil W. Ashcroft, N. David Mermin: Solid State Physics. International Edition. Harcourt, Orlando 1976, S. 643–670, ISBN 0-03-049346-3 (englisch) – Ausführliche theoretische Behandlung von Para- und Diamagnetismus.

Weblinks

• Klassifikation der magnetischen Elemente (englisch) – von der Applied Alloy Chemistry Group der University of Birmingham.
• Quantum Mechanics – The Key To Understanding Magnetism (englisch, PDF) – Vortrag von J. H. Van Vleck zur Nobelpreisverleihung 1977.