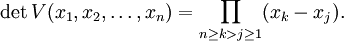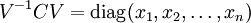- Vandermondematrix
-
Unter einer Vandermonde-Matrix (nach A.-T. Vandermonde) versteht man in der Mathematik eine Matrix, die eine im folgenden beschriebene spezielle Form hat.
Für ein n-Tupel
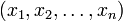 reeller Zahlen oder allgemeiner von Elementen in einem Körper ist die Vandermonde-Matrix definiert durch:
reeller Zahlen oder allgemeiner von Elementen in einem Körper ist die Vandermonde-Matrix definiert durch: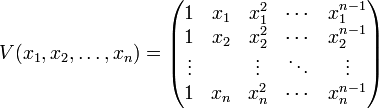
Die Determinante wird auch Vandermonde-Determinante genannt, sie hat den Wert
Insbesondere ist die Vandermonde-Matrix genau dann regulär, wenn die xi paarweise verschieden sind.
Anwendung: Polynominterpolation
Die Vandermonde-Matrix spielt bei der Interpolation von Funktionen eine wichtige Rolle: Um an den Stützstellen
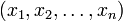 die Funktionswerte
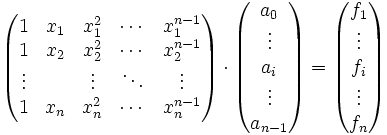
die Funktionswerte 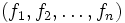 durch ein Polynom vom Grad n − 1 zu interpolieren, muss man das Lineare Gleichungssystem
durch ein Polynom vom Grad n − 1 zu interpolieren, muss man das Lineare Gleichungssystemlösen. Das Interpolationspolynom ist dann
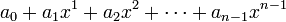 .
.Aus der oben genannten Eigenschaft der Determinante folgt insbesondere, dass das Interpolationsproblem genau dann eindeutig lösbar ist, wenn alle Stützstellen paarweise verschieden sind.
In der Standardbasis der Polynome ist die Matrix allerdings sehr schlecht konditioniert, weswegen man andere Darstellungen für die Polynome wählt.
Die Vandermonde-Matrix diagonalisiert die Begleitmatrix C des Polynoms
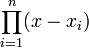 :
:
Wikimedia Foundation.