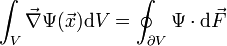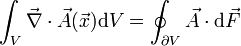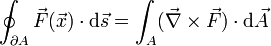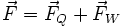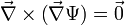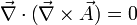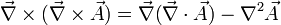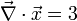- Vektoranalyse
-
Vektoranalysis ist ein Teilgebiet der Mathematik, das sich mit Vektoren in zwei oder mehr Dimensionen beschäftigt. Es besteht aus einem Satz von Formeln und Problemlösungstechniken, die für Ingenieurwesen und Physik sehr nützlich sind.
Betrachtet werden Vektorfelder, die jedem Punkt des Raumes einen Vektor zuordnen, und Skalarfelder, die jedem Punkt des Raumes einen Skalar zuordnen. Die Temperatur eines Swimmingpools ist ein Skalarfeld: Jedem Punkt wird der Skalarwert seiner Temperatur zugeordnet. Die Wasserbewegung in einem Swimmingpool ist dagegen ein Vektorfeld, da jedem Punkt ein Geschwindigkeitsvektor zugeordnet wird.
Die meisten analytischen Ergebnisse sind leichter mit Hilfe der Differentialgeometrie zu verstehen, einer Theorie, die die Vektoranalysis umfasst.
Inhaltsverzeichnis
Gängige Differentialoperatoren
Drei Rechenoperationen sind in der Vektorrechnung von Bedeutung (dabei ist
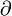 der Operator der partiellen Ableitung):
der Operator der partiellen Ableitung):- Gradient eines Skalarfeldes: Gibt die Richtung und Stärke der Veränderung eines Skalarfeldes an; der Gradient eines Skalarfeldes ist ein Vektorfeld.
- Divergenz eines Vektorfeldes: Gibt die Tendenz eines Vektorfeldes an, zu Punkten hin oder von Punkten weg zu fließen; die Divergenz eines Vektorfeldes ist ein Skalarfeld. Die Divergenz beschreibt somit die lokale Quellendichte eines Vektorfeldes.
- Rotation eines Vektorfeldes: Gibt die Tendenz eines Vektorfeldes an, um Punkte zu rotieren; die Rotation eines Vektorfeldes ist ein Vektorfeld von Pseudovektoren. Die Rotation beschreibt somit die lokale Wirbeldichte eines Vektorfeldes.
Inverse Integraloperatoren
Zu den oben vorgestellten Differentialoperatoren existieren bei entsprechender Definition auch die inversen Integraloperatoren. Sie sind vor allem in der englischen Fachliteratur üblich. Sie ermöglichen unter anderem in der Elektrodynamik in Kombinationen mit den Greenschen Funktionskernen oft einfachere und elegantere Lösungswege. Sie bedürfen analog zu den Differentialoperatoren im konkreten Einzelfall der Anpassung der Integration in einem entsprechenden Koordinatensystem.
- Integraloperator
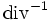 : Der Definitionsbereich des Operators ist die Menge aller Quellendichten
: Der Definitionsbereich des Operators ist die Menge aller Quellendichten 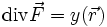 . Sein Wertebereich umfasst die Menge aller Vektorfelder mit verschwindender Wirbelfeldkomponente. Angewandt auf die Quellendichte liefert der Operator
. Sein Wertebereich umfasst die Menge aller Vektorfelder mit verschwindender Wirbelfeldkomponente. Angewandt auf die Quellendichte liefert der Operator 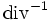 das zugehörige Quellenfeld.
das zugehörige Quellenfeld.
- Integraloperator
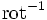 : Der Definitionsbereich des Operators ist die Menge aller Wirbeldichten
: Der Definitionsbereich des Operators ist die Menge aller Wirbeldichten 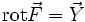 . Sein Wertebereich umfasst die Menge aller Vektorfelder mit verschwindender Quellenfeldkomponente. Angewandt auf die Wirbeldichte liefert der Operator
. Sein Wertebereich umfasst die Menge aller Vektorfelder mit verschwindender Quellenfeldkomponente. Angewandt auf die Wirbeldichte liefert der Operator 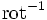 das zugehörige Wirbelfeld.
das zugehörige Wirbelfeld.
- Integraloperator
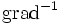 : Der Definitionsbereich des Operators ist die Menge aller Gradientenfelder
: Der Definitionsbereich des Operators ist die Menge aller Gradientenfelder 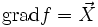 . Sein Wertebereich umfasst die Menge aller Potentialfelder mit verschwindendem ortsunabhängigen Anteil f0. Lässt man alle Potentialfelder zu, besitzt
. Sein Wertebereich umfasst die Menge aller Potentialfelder mit verschwindendem ortsunabhängigen Anteil f0. Lässt man alle Potentialfelder zu, besitzt 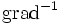 die Eigenschaft eines unbestimmten Integrals mit der dabei auftretenden Integrationskonstante f0.
die Eigenschaft eines unbestimmten Integrals mit der dabei auftretenden Integrationskonstante f0.
Integralsätze
Integralsätze haben insbesondere in der Physik (z. B. Elektrodynamik) eine große Bedeutung.
Satz von Gauß
Das Volumenintegral über eine skalare Größe kann mittels des Gradientbegriffs in ein Oberflächenintegral über dieses Volumen umgewandelt werden:
Dies ist ebenfalls für eine vektorielle Größe möglich, das Integral der Divergenz über das gesamte Volumen ist gleich dem Integral des Flusses über die Oberfläche:
Satz von Stokes
Das geschlossene Wegintegral einer vektoriellen Größe kann mittels der Rotation in ein Flächenintegral über eine vom Integrationsweg eingeschlossene Fläche umgewandelt werden:
Fundamentalsatz der Vektoranalysis
Der Fundamentalsatz der Vektoranalysis, auch Helmholtzscher Zerlegungssatz genannt, beschreibt den allgemeinen Fall, dass sich jedes Vektorfeld
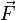 als eine Überlagerung eines Quellenfelds
als eine Überlagerung eines Quellenfelds 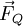 und eines Wirbelfeldes
und eines Wirbelfeldes 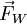 beschreiben lässt:
beschreiben lässt:Ein allgemeines Vektorfeld ist bezüglich seiner physikalischen Bedeutung daher nur dann eindeutig spezifiziert, wenn sowohl Aussagen über die Quellen- als auch Wirbeldichten und ggf. die notwendigen Randwerte vorliegen.
Identitäten
Diese Identitäten erweisen sich oft für Umformungen nützlich:
-
- wird häufig zur Herleitung der Wellengleichung in der Elektrodynamik verwendet.
Folgerung aus dem Verschwinden der Divergenz
Aus
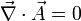 folgt
folgt  mit einem Vektorfeld
mit einem Vektorfeld 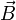 .
.Folgerung aus dem Verschwinden der Rotation
Aus
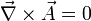 folgt
folgt 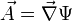 mit einem Skalarfeld Ψ.
mit einem Skalarfeld Ψ.Siehe auch
Literatur
- Klaus Jänich: Vektoranalysis Springer, Berlin März 2005, ISBN 3540237410
- Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler Band 3. Vektoranalysis, Wahrscheinlichkeitsrechnung [...], Vieweg Verlag Januar 2001, ISBN 3528349379
- M. Schneider: Über die Verwendung der Operatoren div-1, rot-1, grad-1 in der Feldtheorie, Archiv für Elektrotechnik, Springer Verlag, 1997
Weblinks
Wikimedia Foundation.

![\operatorname{grad}~\varphi:=\vec \nabla\varphi = \begin{pmatrix} \frac{\partial\varphi} {\partial x} \\[0.2cm] \frac{\partial\varphi}{\partial y} \\[0.2cm] \frac{\partial\varphi}{\partial z} \end{pmatrix}](/pictures/dewiki/56/8076a833d431148a8c3d55cecca67e16.png)
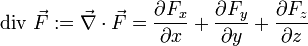
![\operatorname{rot}~\vec F := \vec \nabla\times\vec F =
\begin{pmatrix}
\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z} \\[0.2cm]
\frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x} \\[0.2cm]
\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}
\end{pmatrix}](/pictures/dewiki/48/09dd2c3b822ec79c94ff6a4e520f6dd5.png)