Vektorautoregressives Modell

Vektorautoregressive Modelle (kurz VAR-Modelle) sind sehr weit verbreitete ökonometrische Modelle zum simultanen Schätzen mehrerer Gleichungen. Sie gehören zu der Modelloberklasse der VARMA-Modelle. Bei dieser Art von Zeitreihenmodellen werden die endogenen Variablen sowohl durch ihre eigenen Vergangenheitswerte (Zufallsschock), als auch durch die Vergangenheitswerte der anderen endogenen Variablen bestimmt. Die Variablen werden deshalb auch als verzögert exogen bezeichnet. Es gibt also eine Rückkopplung zwischen den Variablen, wenn die Kovarianzmatrix nicht-diagonal ist.

Abgrenzung zu Transferfunktionsmodellen

Es gibt Ähnlichkeiten zwischen den VAR-Modellen und den Transferfunktionsmodellen. Ein VAR(1)-Modell darf aber nicht als kausales Transferfunktionsmodell angesehen werden. Grund ist die jeweilige kontemporäre Korrelierung der Schockvariablen. Durch die Orthogonalisierung der Schockvariablen (Diagonalisierung der Varianz-Kovarianzmatrix) kann ein VAR(1)-Modell trotzdem in ein kausales Transferfunktionsmodell umgewandelt werden.

Der Aufbau einer VAR-Schätzung

$X_t = \nu + A_1 \cdot X_{t-1} + A_2 \cdot X_{t-2} + ... + A_q \cdot X_{t-q} + B \cdot Z_t+ \epsilon_t$

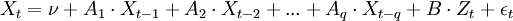
Wobei X_t den Vektor der endogenen Variablen, Z_t den Vektor der exogenen Variablen und u_t den Fehlerterm bezeichnet.

Zur Wahl der optimalen Anzahl von Verzögerungen (optimale Lagordnung) können das Akaike- oder das Schwarz-Kriterium herangezogen werden. Es ist zu beachten, dass jede hinzugenommene Verzögerung zwar weiteren Erklärungsgehalt bringt, jedoch gleichzeitig Freiheitsgrade wegfallen, womit die Schätzung von der Empirie immer weiter entfernt wird. Das Akaike-Kriterium überschätzt die Anzahl der Verzögerungen, das Schwarz-Kriterium ist zu sparsam.

Wichtig ist, dass die Zeitreihen trendbereinigt (etwa mit Hodrick-Prescott-Filter) und stationär sein müssen. Dies ist der Fall, wenn alle Nullstellen der Hilfsgleichung außerhalb des Einheitskreises liegen.

Die Berechnung der Kovarianzmatrix erfolgt rekursiv. Helmut Lütkepohl entwickelte ein einfache Methode für die Berechnung der Startmatrizen.

Kritik an VAR

VAR-Modelle sind nicht theoriefundiert, sie geben einen rein statistischen Zusammenhang wieder. Die Wahl der Zeitreihe, des Zeitraums und der Impulsreihenfolge (siehe hierzu Cholesky-Zerlegung) sind frei und können deshalb zu mangelnder Robustheit der Ergebnisse führen. Zum Teil weisen VAR-Modelle Zusammenhänge nach, die nicht durch die gegenseitige Beeinflussung der Variablen, sondern auch durch eine gemeinsame Reaktion auf dritte, nicht hinzugenommene, Variablen hervorgerufen werden können. Auch stellt eine Hinzunahme nur einer Variablen, je nach Lagordnung bereits eine erhebliche Verkomplizierung des Modells dar, weswegen VARs auf relativ kleine Modelle beschränkt bleiben. Die Ergebnisse von VAR-Schätzungen sollten deshalb sehr genau geprüft werden.