Vieleweltentheorie

Die Viele-Welten-Interpretation (engl. many-worlds interpretation oder MWI) ist eine realistische Interpretation der Quantenmechanik von Hugh Everett III, welche die unterschiedlichen überlagerten Zustände, die sich in der Zeitentwicklung eines quantenmechanischen Systems üblicherweise zwischen zwei Beobachtungen ergeben, als in unterschiedlichen, real existierenden Welten realisiert, versteht.

Kopenhagener Deutung

Wie andere Interpretationen der Quantenmechanik versucht auch die Viele-Welten-Interpretation, dem mathematischen Formalismus dieser Mechanik eine ontologische Bedeutung zuzuordnen. Motivierend war für Hugh Everett ein Aspekt der heute wie damals von den meisten Wissenschaftlern akzeptierten Kopenhagener Deutung, die Existenz überlagerter Zustand bis zum so genannten Kollaps der Wellenfunktion.

In der Kopenhagener Deutung kann die Zeitentwicklung eines Systems auf zwei verschiedene Arten erfolgen: Kontinuierlich, der Schrödinger-Gleichung gehorchend, oder diskontinuierlich bei einem Messprozess. Sobald man einen quantenphysikalischen Zustand einer Messung unterzieht, kollabiert der überlagerte Zustand in einen so genannten Eigenzustand des Messoperators. Die Wahrscheinlichkeit dafür, einen bestimmten dieser diskreten Zustände zu beobachten, ist dabei mittels der Bornschen Regel quantifizierbar. Der Kollaps geschieht abrupt ohne Zeitverzögerung; außerdem kann die Störung, welche durch den Messprozess am System vorgenommen wird, beliebig schwach sein.

Albert Einstein, welcher den Kollaps als spukhafte Fernwirkung betitelte, empfand diesen postulierten Kollaps als unelegant. Ein häufig geäußerter Kritikpunkt ist, dass es im Rahmen der Kopenhagener Interpretation keine klare Definition gibt, ab wann ein Prozess als Messung zählt, also einen Kollaps herbeiführt, und wann man noch mit der Schrödinger-Gleichung rechnen kann.

Der Interpretationsansatz von Everett

Everett argumentiert, dass der anscheinende Kollaps der Wellenfunktion nur unserer subjektiven Perspektive geschuldet, genau genommen aber eine Illusion ist. Er geht von folgenden Annahmen aus:

1. Die Wellenfunktion ist nicht nur einfach eine Beschreibung des Zustands eines Objektes, sondern sie ist das Objekt. Diese Annahme teilt sie mit anderen Interpretationen.
2. Und zwar sind die unterschiedlichen Eigenzustände, die sich gemäß der Wellenfunktion überlagern, tatsächlich in unterschiedlichen Welten realisiert.
3. Beobachtung spielt keine spezielle Rolle, anders als z. B. in der Kopenhagener Interpretation.

Nachdem Everett die von Ihm so bezeichnete "Theorie der universalen Wellenfunktion" 1957 veröffentlichte^[1], wurde sie von der physikalischen Gemeinde schlichtweg ignoriert. Heute gilt sie dagegen als ernsthafte Alternative.

In der Viele-Welten-Interpretation gilt die Schrödingergleichung immer und überall uneingeschränkt. Eine Beobachtung oder Messung eines Objekts durch einen Beobachter wird beschrieben, indem die Schrödingergleichung auf das Gesamtsystem aus Beobachter und Beobachtetem angewendet wird. Eine Folge ist, dass jede Beobachtung die Wellenfunktion dazu bringt, in mehrere nicht miteinander wechselwirkende „Zweige“ oder „Welten“ zu dekohärieren. Da ununterbrochen viele beobachtungsartige Prozesse passieren, gibt es eine enorme Menge gleichzeitig existierender Welten.

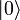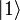Als Beispiel zur Verdeutlichung betrachten wir die quantenmechanische Beschreibung eines Spin-½-Teilchens. Die zwei Basiszustände sind dann spin-up und spin-down, die wir mit $|0\rangle$ und $|1\rangle$ bezeichnen.

Der Zustand eines solchen Spins ist dann eine Überlagerung dieser beiden Zustände, also

$|\psi\rangle = a|0\rangle + b|1\rangle$

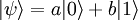
Eine Messung des Spins liefert nun mit Wahrscheinlichkeit | a | ² das Ergebnis 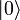$|0\rangle$ und mit Wahrscheinlichkeit | b | ² das Ergebnis 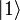$|1\rangle$. In diesem Punkt stimmen die Viele-Welten-Interpretation und die Kopenhagener Deutung überein. Der Unterschied liegt im Zustand nach der Messung. 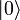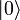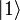Wenn das Ergebnis der Messung $|0\rangle$ war, so sagt die Kopenhagener Deutung, dass der ursprünglich aus $|0\rangle$ und $|1\rangle$ zusammengesetzte Zustand auf den Zustand 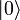$|0\rangle$ kollabiert. Die Messung hat den Zustand also auf einen der beiden Basiszustände festgelegt.

Everett war der Ansicht, dass eine solche Deutung nicht in der Lage sei, das gesamte Universum korrekt zu beschreiben, weil bei ihr der Beobachter nicht mit zum System gerechnet wird. Er schlug vor, das Wissen des Beobachters als Zustand mit in die Beschreibung des Systems aufzunehmen. Der ursprüngliche überlagerte Zustand hätte dann die Form

$|\text{Beobachter kennt den Spin nicht}\rangle \otimes (a|0\rangle + b|1\rangle)$

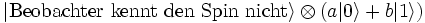
Nach der Messung ist das System dann im Zustand

$a|\text{Beobachter hat 0 gemessen}\rangle\otimes|0\rangle + b|\text{Beobachter hat 1 gemessen}\rangle\otimes|1\rangle$

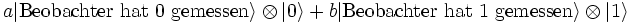
Wie man sieht, findet hier kein Kollaps statt. Vielmehr befindet sich das System auch nach der Messung in einem überlagerten Zustand, bei dem der Beobachter je nach Basiszustand glaubt, 0 oder 1 gemessen zu haben.

In Everetts ursprünglicher Arbeit gibt er jedoch keine Auskunft darüber, wie diese Überlagerung interpretiert werden muss. Die auf dieser Arbeit aufbauende Viele-Welten-Interpretation besagt, dass jedem Summanden dieser Überlagerung genau ein Universum entspricht, in welchem der entsprechende Zustand realisiert ist. Diese einfache Erklärung ist jedoch nicht in der Lage, die Unterschiede in den Erwartungswerten zu erklären.^[2]

Der Ausdruck „viele Welten“ stammt von Bryce DeWitt, der mehr zum Thema von Everetts originaler Arbeit schrieb. Diese spezielle Version wurde so populär, dass sie des Öfteren mit Everetts Originalarbeit verwechselt wird. Einer der populärsten Verfechter der Theorie ist im Moment David Deutsch.

Verschränkte Zustände

Betrachtet man ein System, das aus zwei oder mehr Teilsystemen aufgebaut ist, so werden Zustände des Gesamtsystems, in denen jedes Teilsystem in einem bestimmten Zustand ist, durch die Produkte der Einzelsystemzustände dargestellt. Neben diesen Produktzuständen hat das Gesamtsystem jedoch noch weitere Zustände, so genannte verschränkte Zustände, die Superpositionen der Produktzustände sind und in denen die Teilsysteme für sich keinen definierten Zustand besitzen. Da es viel mehr verschränkte Zustände als Produktzustände gibt, wird sich das Gesamtsystem typischerweise in einem solchen verschränkten Zustand befinden. Jedoch selbst wenn das System sich ursprünglich in einem Produktzustand befand, wird eine Wechselwirkung zwischen den Teilsystemen unweigerlich dazu führen, dass das System in einen verschränkten Zustand übergeht.

Da sich jedoch ein verschränkter Zustand als Superposition von Produktzuständen verstehen lässt, kann der Zustand eines Systems relativ zum anderen angegeben werden (z. B. bei zwei Spin-½-Teilchen, deren Spins sich zu Null addieren, ist die Richtung der Einzelspins nicht festgelegt, die relative Richtung der beiden Spins jedoch schon – die beiden Spins zeigen in die entgegengesetzte Richtung). Deshalb sprach Everett auch von relativen Zuständen.

Da die Schrödingergleichung eine lineare Differentialgleichung ist, ist die Zeitentwicklung der einzelnen Summanden der Superposition unabhängig voneinander. Das bedeutet, dass man die Zeitentwicklung eines verschränkten Zustandes bestimmen kann, indem man getrennt die Entwicklung der einzelnen Produktzustände betrachtet. Der Gesamtzustand zu einem späteren Zeitpunkt ergibt sich dann einfach wieder als dieselbe Superposition der zeitentwickelten Summanden. Wenn die verschiedenen Summanden verschiedene Realitätszweige (Welten) beschreiben, so bedeutet dies, dass die Zeitentwicklung eines Realitätszweiges nicht davon abhängt, ob daneben ein anderer Realitätszweig existiert.

Vergleich mit der Kopenhagener Interpretation

Dieser Artikel oder Abschnitt ist nicht hinreichend mit Belegen (Literatur, Webseiten oder Einzelnachweisen) versehen. Die fraglichen Angaben werden daher möglicherweise demnächst gelöscht. Hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Bitte entferne erst danach diese Warnmarkierung.

Mathematisch und physikalisch ist die Viele-Welten-Interpretation einfacher als die Kopenhagener Interpretation. Der Vorgang des Messens oder Beobachtens hat keinen Sonderstatus, und die Interpretation des Quadrats des Amplitudenbetrags der Wellenfunktion als Wahrscheinlichkeit ist eine Folgerung der Theorie, anstatt ein notwendiges Axiom. Allerdings lehnen viele Physiker die Folgerung nicht beobachtbarer alternativer Universen auf der Basis von Ockhams Rasiermesser ab (beide Seiten argumentieren mit Ockhams Rasiermesser, wenden es aber an unterschiedlichen Stellen an). Einige Physiker haben festgestellt, dass die Unterstützung für die Viele-Welten-Interpretation zunimmt, vor allem deshalb, weil sich aus ihr Voraussagen zum Prozess der Quanten-Dekohärenz in einer natürlichen Weise zu ergeben scheinen, statt dass sie in Ad-hoc-Manier hinzugefügt werden müssen.

Dennoch gibt es bis heute (Stand 2007) keine praktischen Experimente, die zwischen der Kopenhagener und der Viele-Welten-Interpretation entscheiden könnten, und ohne Beobachtungsdaten ist die Wahl eine Frage des persönlichen Geschmacks. Allerdings ist der Entwurf von Experimenten, die zwischen verschiedenen Interpretationen der Quantenmechanik unterscheiden könnten, ein aktives Forschungsgebiet. So beruht zum Beispiel ein Vorschlag darauf, dass in einer Welt mit unendlich vielen alternativen Universen diejenigen, die kollabieren, eine kürzere Zeit lang existieren würden als diejenigen, die expandieren, und dass dies beobachtbare Unterschiede in bestimmten Wahrscheinlichkeiten zwischen der Viele-Welten- und der Kopenhagener Interpretation ergeben sollte.

Die Viele-Welten-Interpretation sollte nicht mit der Many-Minds-Interpretation verwechselt werden, die postuliert, dass sich nicht die ganze Welt, sondern nur das Bewusstsein des Beobachters spaltet.

Siehe auch

• Interpretationen der Quantenmechanik - für andere Interpretationen
• Multiversum
• Kopenhagener Deutung
• Kollaps der Wellenfunktion
• Quantenselbstmord

Einzelnachweise

1. ↑ Hugh Everett, III: “Relative State” Formulation of Quantum Mechanics. In: Rev. Mod. Phys.. 29, 1957, S. 454–462 (doi:10.1103/RevModPhys.29.454). 
2. ↑ Vgl. z.B. Hilary Putnam: A Philosopher Looks at Quantum Mechanics. in: Robert G. Colodny (Hg.): Beyond the Edge of Certainty: Essays in Contemporary Science and Philosophy, Englewood Cliffs, N.J.: Prentice-Hall, 1965, 75-101, Wiederabdruck in Putnam: Mathematics, Matter and Method, Cambridge, Mass., Cambridge University Press 1975, 130-158.

Weblinks

• Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und weder Parameter 2 noch Parameter 3
• Everett's Relative-State Formulation of Quantum Mechanics. Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und weder Parameter 2 noch Parameter 3
• Wozu braucht man "Viele Welten" in der Quantentheorie?, Prof. Dieter Zeh
• 4 Ebenen der Paralleluniversen von Max Tegmark