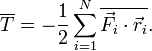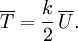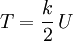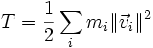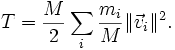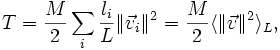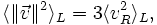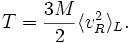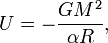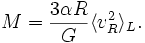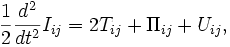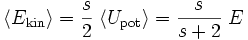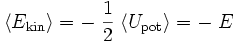- Virialtheorem
-
Der Virialsatz (lat. vis „Kraft“) ist eine Beziehung zwischen dem zeitlichen Mittel der kinetischen Energie
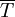 und dem zeitlichen Mittel der potentiellen Energie
und dem zeitlichen Mittel der potentiellen Energie 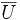 eines abgeschlossenen physikalischen Systems.
eines abgeschlossenen physikalischen Systems.Inhaltsverzeichnis
Formulierung
Das Virial V eines Systems aus N Teilchen ist die Summe der Skalarprodukte aus den Impulsen und Orten dieser Teilchen, d.h.
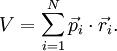 Der Vektor
Der Vektor 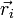 beschreibt den Ort, der Vektor
beschreibt den Ort, der Vektor 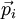 den Impuls des i-ten Teilchens. Ist das Virial beschränkt, so gilt die Beziehung:
den Impuls des i-ten Teilchens. Ist das Virial beschränkt, so gilt die Beziehung:Dabei ist
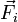 die Resultierende der auf das i-te Teilchen einwirkenden Kräfte, die von anderen Teilchen des Systems ausgeübt werden. Da ein abgeschlossenes System betrachtet wird, existieren keine äußeren Kräfte.
die Resultierende der auf das i-te Teilchen einwirkenden Kräfte, die von anderen Teilchen des Systems ausgeübt werden. Da ein abgeschlossenes System betrachtet wird, existieren keine äußeren Kräfte.Ist die Kraft konservativ und besitzt ein Potential U, das homogen vom Grad k ist, d.h. für α > 0 gilt
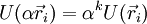 , so vereinfacht sich die obige Form auf
, so vereinfacht sich die obige Form aufBefindet sich ein Vielteilchensystem im Gleichgewicht, so kann das System als ergodisch betrachtet werden, d.h. das Zeitmittel ist gleich dem Scharmittel für alle Beobachtungsgrößen. Da dies insbesondere für die kinetische und die potentielle Energie gilt und das Scharmittel der Energien einfach aus der Summe der Einzelenergien geteilt durch die Anzahl der Objekte N gebildet wird, lässt sich das Scharmittel durch die Gesamtenergien ausdrücken. Wir erhalten daher für Gleichgewichtssysteme:
ohne Mittelung über die Zeit, denn die Werte sind zeitlich konstant.
Anwendungsbeispiel
Anwendung findet der Virialsatz beispielsweise in der Astrophysik und der Himmelsmechanik. Dort benutzt man das Newton'sche Gravitationspotential, das homogen vom Grad -1 ist. Es gilt dann
- 2T = − U.
Der Virialsatz erlaubt es, recht gute Abschätzungen für die Gesamtmassen dynamisch gebundener Systeme wie Sternhaufen oder Galaxienhaufen zu finden. Die Gesamtmasse eines solchen Haufens kann dann vollständig durch Beobachtungsgrößen wie Radialgeschwindigkeiten, Winkelabstände und scheinbare Helligkeiten der Einzelobjekte ausgedrückt werden. Die einzige Voraussetzung für die Anwendung des Virialsatzes ist die Kenntnis des Abstandes des Haufens. Wir wollen das Vorgehen bei einer Massenbestimmung eines solchen Haufens hier skizzieren:
- Die kinetische Gesamtenergie eines Stern- oder Galaxienhaufens ist durch
- gegeben. Weder die Einzelmassen mi noch die Geschwindigkeitsbeträge |vi| sind jedoch Beobachtungsgrößen. Die Einführung der Gesamtmasse
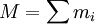 erlaubt die einfache Umformung
erlaubt die einfache Umformung
- Macht man nun die zwei Annahmen:
- a) Die Einzelmassen mi sind proportional zu den Einzelleuchtkräften li und daher gilt
- wobei der letzte Term das Leuchtkraft-gewichtete Mittel über die Geschwindigkeiten bezeichnet.
- b) Das System ist sphärisch symmetrisch und befindet sich im Gleichgewicht (man sagt auch es ist virialisiert). Daher sind die Geschwindigkeiten über die Raumrichtungen gleichverteilt (Gleichverteilungssatz). Es gilt dann
- wobei vR die radialen Pekuliargeschwindigkeiten bezeichnet, d.h. die Abweichungen der Radialgeschwindigkeit vom Haufenmittelwert. Damit erhält man:
- Für die potentielle Gesamtenergie gilt unter der Bedingung der sphärischen Symmetrie
- wobei R der Gesamtradius des System ist und der morphologische Faktor α von der radialen Verteilungsfunktion, also der Geometrie des Haufens abhängt. Für eine (allerdings unrealistische) Gleichverteilung innerhalb des Radius R ist beispielsweise α=5/3. Im Allgemeinen ist der Faktor aus den Winkelabständen der Einzelsysteme zum Haufenzentrum zu bestimmen.
- Für die Gesamtmasse des Haufens erhalten wir somit die Formel
Verallgemeinerung
Im Rahmen der Kontinuumsmechanik wird der tensorielle Virialsatz aus der stoßfreien Boltzmann-Gleichung und dem daraus abgleiteten Jeans-Kriterium bewiesen. Wenn als Wechselwirkung wiederum die Gravitation angenommen wird, hat der Satz die Form:
wobei Iij der Trägheitstensor, Tij der kinetische Energietensor, Πij der Spannungstensor und Uij der potentielle Energietensor ist. Im statischen Fall fällt die Zeitableitung auf der linken Seite der Gleichung weg und die Spur der Gleichung ergibt wieder den skalaren Virialsatz, da der Spannungstensor spurfrei ist.
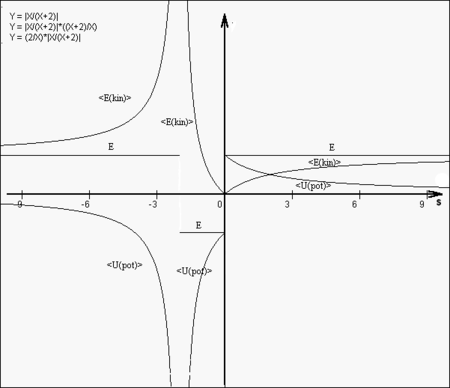
Vorzeichen von Energiegrößen im Virialsatz
Der Virialsatz in der allgemeinen Form für eine homogene Potentialfunktion vom Grad s
gibt eindeutige Auskunft über die richtigen Vorzeichen der beteiligten Energiegrößen.
Für den bekanntesten Fall s = − 1 (Gravitation, Coulombsches Kraftgesetz) ergibt sich beispielsweise:
Die Vorzeichen im einzelnen sind (s. Abb.):
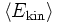 ist positiv definit.
ist positiv definit.
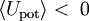 für
für 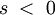 und
und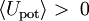 für
für 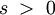 .
.
- Und
- E > 0 für s < − 2 oder 0 < s.
- E < 0 für − 2 < s < 0.
Literatur
- Rudolf Clausius: Ueber einen auf die Wärme anwendbaren mechanischen Satz, Annalen der Physik (Zeitschrift), 1870, Vol. 217, Issue 9, Seiten 124–130, Text
- Lew Dawidowitsch Landau, Jewgeni Michailowitsch Lifschitz: Mechanik (Lehrbuch der theoretischen Physik; Bd. 1). Deutsch, Frankfurt/M. 2004, ISBN 3-8171-1326-9
- Gibt eine einfache Herleitung des skalaren Virialsatzes.
- James Binney, Scott Tremaine: Galactic Dynamics Princeton Series in Astrophysics. Princeton University Press, Princeton, N.J. 1988, ISBN 0-691-08445-9
- Hier findet man die tensorielle Verallgemeinerung und Anwendungen.
Einzelnachweise und Bemerkungen
- ↑ Die spitzen Klammern stehen bekannterweise für gemittelte Werte, für ein stationäres System von Punktteilchen, welche sich in dynamischem Gleichgewicht bewegen.
- ↑ Heinrich Wulff, Physik unter Verwendung des Virialsatzes, Grafik & Typographie, 1998 ISBN 3-9804816-0-3
Weblinks
Wikimedia Foundation.