Voigtprofil

Unter dem Voigt-Profil oder auch der Voigtfunktion (nach Woldemar Voigt) versteht man die Faltung einer Gauß-Kurve G(x) mit einer Lorentz-Kurve L(x). Eine oft verwendete Näherung ist die Pseudo-Voigtfunktion.

Mathematische Beschreibung

$V(x) = (G*L)(x) = \int G(\tau)L(x-\tau)d\tau$

$G(x)=\frac{e^{-x^2/(2\sigma^2)}}{\sigma \sqrt{2\pi}}$

$L(x)=\frac{\gamma}{\pi(x^2+\gamma^2)}.$

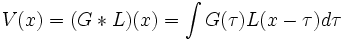
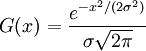
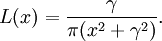
σ entspricht der Standardabweichung einer Gauß-Verteilung. In der Spektroskopie wird sie mit Dopplerbreite bezeichnet. γ ist die halbe Halbwertsbreite der Lorentzverteilung, in der Spektroskopie als Druckverbreitung bekannt. Das Voigt-Profil entsteht aus der Faltung des Gauß-Profils mit dem Lorentz-Profil. Das Voigt-Profil ist wie jeweils das Gauß- und Lorentz-Profil auf 1 normiert (Fläche unter den Profilen).

Numerische Darstellung

Für das Faltungsintegral V(x) existiert keine analytische Lösung, doch kann es als Realteil der imaginären Fehlerfunktion w(z) ausgedrückt werden, für die hinreichend gute Näherungen verfügbar sind:

$V(x)=\frac{\textrm{Re}\left[w(z)\right]}{\sigma\sqrt{2 \pi}}.$

z ist hier definiert als

$z=\frac{x+i\gamma}{\sigma\sqrt{2}}.$

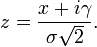
Die Breite des Voigt-Profils

Das FWHM des Vogt-Profils lässt sich aus den Breiten der beteiligten Lorentz- und Gauß-Kurven bestimmen. Bekannt ist die Breite des Gauß-Profils:

$f_\mathrm{G}=2\sigma\sqrt{2\ln(2)}.\,$

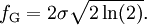
und die Breite des Lorentz-Profils:

f_L = 2γ

Dann gilt näherungsweise:

$f_\mathrm{V}\approx f_\mathrm{G}\left(1-c_0c_1+\sqrt{\phi^2+2c_1\phi+c_0^2c_1^2}\right)$

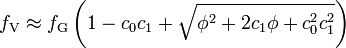
mit φ = f_L / f_G, c₀=2,0056 und c₁=1,0593. Diese Abschätzung hat einen relativen Fehler von etwa 2,4 % für Werte φ zwischen 0 und 10. Obige Gleichung liefert für die Grenzwerte φ = 0 und 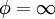$\phi = \infty$ das korrekte Verhalten.

Eine alternative Näherung ist die Formel nach Olivero and Longbothum ^[1].

$f_\mathrm{V}\approx 0{,}5346 f_\mathrm{L}+\sqrt{0{,}2166f_\mathrm{L}^2+f_\mathrm{G}^2},$

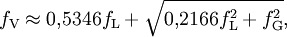
die mit einer Genauigkeit von 0,02 % angegeben ist.

Eigenschaften

Die Voigt-Funktion ist invariant gegenüber Faltung, d. h., die Faltung einer Voigtfunktion mit einer Voigt-Funktion ergibt wieder eine Voigtfunktion. Die Linienbreiten des Gauß- bzw. Lorentz-Anteils ergeben sich dabei zu: $f_{G}^{2} = \sum_{i}{(f_{G}^{2})_{i}} ; f_{L} = \sum_{i}{(f_{L})_{i}}$.

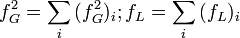Einzelnachweise und Fußnoten

1. ↑ Olivero, J. J. ; Longbothum, R. L.: Empirical fits to the Voigt line width: A brief review. In: J. Quant. Spectrosc. Radiat. Transfer 17 (1977), Nr. 233-236, S. 12–98