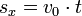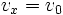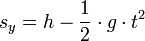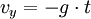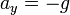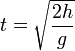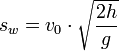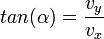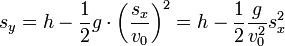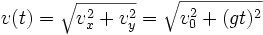Waagrechter Wurf

Unter dem Waagerechten Wurf versteht man in der Physik den Bewegungsvorgang, den ein Körper vollzieht, wenn er parallel zum Horizont geworfen wird. Der Vorgang lässt sich nach dem Unabhängigkeitsprinzip in zwei Teilbewegungen zerlegen. Dies funktioniert aber nur dann, wenn man den Wurf unter idealisierten Bedingungen, also z. B. ohne Berücksichtigung des Luftwiderstandes betrachtet.

Die Analyse der Bewegungen

In waagerechter x-Richtung

Wird ein Körper z. B. von einem Tisch gestoßen, verlässt der Körper diesen mit der konstanten Geschwindigkeit v₀ in horizontaler Richtung. Es gelten also die Gesetze der gleichförmigen Bewegung:

$s_x=v_0\cdot t$

$v_x=v_0\,$

In senkrechter y-Richtung

Gleichzeitig fällt der Körper aus der Höhe h nach unten. Es gelten die Gesetze des Freien Falls:

$s_y=h-\frac{1}{2}\cdot g\cdot t^2$

$v_y=-g\cdot t$

$a_y=-g\,$

Wurfzeit

Setzt man die s_y-Gleichung mit 0 gleich und löst sie nach t auf, so erhält man die Zeit, die der Körper braucht, um auf den Boden zu fallen:

$t=\sqrt{\frac{2h}{g}}$

Wurfweite

Nun kann man die Formel für die Wurfzeit in die s_x-Gleichung einsetzen und erhält so die Wurfweite.

$s_w=v_0\cdot \sqrt{\frac{2h}{g}}$

Aufprallwinkel

Wenn man den Winkel der Bahnkurve zur Horizontalen mit α bezeichnet, dann kann man diesen Winkel aus der folgenden Beziehung berechnen:

$tan(\alpha)=\frac{v_y}{v_x}$

Gleichung der Wurfparabel

Graph der Wurfparabel

Für die Gleichung der Wurfparabel löst man die s_x-Gleichung nach t auf und setzt den Term für t in die s_y-Gleichung ein. So erhält man:

$s_y=h-\frac{1}{2}g\cdot \left(\frac {s_x}{v_0} \right)^2=h-\frac{1}{2} \frac{g}{v_0^2} s_x^2$

Bahngeschwindigkeit

Der Betrag der Bahngeschwindigkeit v(t) errechnet sich mit dem Satz des Pythagoras:

$v(t)=\sqrt{v_x^2+v_y^2}=\sqrt{v_0^2+(gt)^2}$

Siehe auch

• Wurfparabel
• Freier Fall

Weblinks

• Versuche und Aufgaben zum waagerechten Wurf