Walsersort

Slowsort (von engl. slow: langsam) oder auch Walsersort ist ein langsamer, rekursiver, stabiler Sortieralgorithmus, der nach dem Prinzip Vervielfache und kapituliere (engl. Multiply and surrender, eine Parodie auf Teile und herrsche) arbeitet. Er wurde 1986 von Andrei Broder und Jorge Stolfi in ihrer (nicht ganz ernst gemeinten) Veröffentlichung Pessimal Algorithms and Simplexity Analysis[1] vorgestellt. Inzwischen wird Slowsort in der Informatik-Ausbildung verwendet.^[1]

Prinzip

Slowsort ist ein rekursiver Algorithmus, der in folgenden Schritten arbeitet:

• (1) Bestimme das Maximum der zu sortierenden Liste.
• (2) Sortiere den Rest.

Dabei wird der erste Schritt nach dem Prinzip Vervielfache und kapituliere in mehrere geringfügig einfachere Schritte unterteilt:

• (1.1) Bestimme das Maximum der ersten Hälfte der zu sortierenden Liste: Wähle das letzte Element der (rekursiv) sortierten ersten Hälfte.
• (1.2) Bestimme das Maximum der zweiten Hälfte der zu sortierenden Liste: Wähle das letzte Element der (rekursiv) sortierten zweiten Hälfte.
• (1.3) Bestimme das Maximum der beiden Teilmaxima.

Dies wird rekursiv wiederholt, bis die Teillisten nur noch ein einziges Element enthalten und die Lösung somit nicht weiter hinausgezögert werden kann.

Komplexität

Slowsort ist im Gegensatz zu Quicksort stabil. Seine untere asymptotische Grenze für die Laufzeit beträgt in der Landau-Notation ausgedrückt 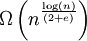$\Omega\left(n^{ \frac{\log(n)}{(2+e)}}\right)$, der Algorithmus lässt sich also nicht in Polynomialzeit ausführen. Slowsort ist somit auch im best case ineffizienter als z. B. Bubblesort mit einer Komplexität von $\mathcal{O}( n^2 )$.

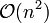Einzelnachweise

1. ↑ Ripon College (Wisconsin): CS336 Lab 8-Sorting Algorithms, Spring 2002 (englisch)

Weblinks

• Wissenschaftliche Veröffentlichung von Broder und Stolfi