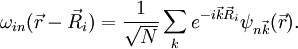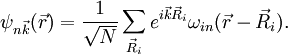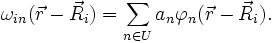Wannierfunktion

Dreidimensionales Modell der Wannier-Funktion von BaTiO₃.

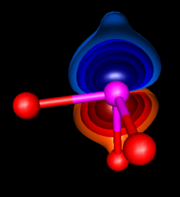
Die nach dem schweizer Physiker Gregory Hugh Wannier benannte Wannier-Darstellung ist ein Begriff aus der Festkörperphysik. In der Tight-Binding-Näherung ist eine Beschreibung der elektronischen Wellenfunktionen in der gitterperiodischen Bloch-Basis nicht mehr sinnvoll. Eher konstruiert man die Zustandsfunktion aus atomaren Wellenfunktionen. Diese sind aber nicht orthonormiert. Es lässt sich jedoch eine Ortonormal-Basis lokalisierter Zustände aus den Bloch-Funktionen konstruieren.

$\omega_{i n}(\vec r -\vec R_i) = \frac{1}{\sqrt{N}}\sum_k e^{-i \vec k \vec R_i} \psi_{n \vec k} (\vec r) .$

Dabei ist 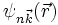$\psi_{n \vec k} (\vec r )$ eine Bloch-Funktion und 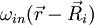$\omega_{i n} (\vec r -\vec R_i)$ der zugehörige Wannier-Zustand. Die umgekehrte Konstruktion der Bloch-Zustände aus den Wannier-Zuständen heißt dann

$\psi_{n \vec k} (\vec r) = \frac{1}{\sqrt{N}}\sum_{\vec R_i} e^{i \vec k \vec R_i} \omega_{i n}(\vec r -\vec R_i).$

Je größer die Gitterkonstante ist, desto stärker sind die Wannierzustände lokalisiert. Sie nähern sich immer mehr an die atomaren Zustände an. Statt aber den Wannier-Zustand einfach einem atomaren Zustand gleichzusetzen, nähert man ihn durch eine Linearkombination von atomaren Zuständen (LCAO):

$\omega_{i n}(\vec r -\vec R_i) = \sum_{n\in U} a_n \varphi_n (\vec r -\vec R_i).$

Die Menge U stellt dabei einen Unterraum der atomaren Zustände 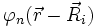$\varphi_n(\vec r -\vec R_i)$ dar.