Webbed space

Räume mit Gewebe werden in der mathematischen Disziplin der Funktionalanalysis betrachtet. Sie erlauben im Zusammenspiel mit den ultrabornologischen Räumen Verallgemeinerungen zweier zentraler Sätze aus der Theorie der Banachräume, das sind der Satz über die offene Abbildung und der Satz vom abgeschlossenen Graphen. Diese Räume wurden 1969 von Marc de Wilde zu genau diesem Zweck eingeführt.

Die Definition ist sehr technisch, aber in vielen Anwendungen kann von den speziellen technischen Gegebenheiten abgesehen werden, da man zeigen kann, dass große Klassen von topologischen Vektorräumen diese Eigenschaft haben, und dass daher die Verallgemeinerungen der genannten Sätze gelten, und diese sind in den Anwendungen wesentlich.

Räume mit Gewebe kann man für beliebige topologische Vektorräume definieren. Es werden hier aus Gründen der einfacheren Darstellung nur lokalkonvexe Räume betrachtet. Die allgemeine Theorie für topologische Vektorräume wird im unten angegebenen Lehrbuch von H. Jarchow behandelt.

Gewebe

Ein Gewebe in einem lokalkonvexen Raum E ist eine Familie von Teilmengen 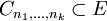$C_{n_1,\ldots,n_k}\subset E$, wobei 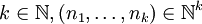$k\in {\mathbb N}, (n_1,\ldots,n_k) \in {\mathbb N}^k$, so dass folgendes gilt:

1. Jede Menge 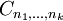$C_{n_1,\ldots,n_k}$ ist absolukonvex und nicht leer.
2. $\bigcup_{n=1}^{\infty} C_{n} = E$.
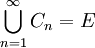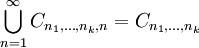3. $\bigcup_{n=1}^{\infty} C_{n_1,\ldots,n_k,n} = C_{n_1,\ldots,n_k}$ für alle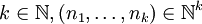 $k\in {\mathbb N}, (n_1,\ldots,n_k) \in {\mathbb N}^k$
4. Für jede Folge (n_k)_k natürlicher Zahlen gibt es eine Folge (λ_k)_k positiver reeller Zahlen, so dass die Reihe 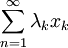$\sum_{n=1}^\infty \lambda_k x_k$ für jede Wahl von Punkten 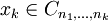$x_k \in C_{n_1,\ldots,n_k}$ konvergiert.

Man kann sich die Mengen 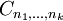$C_{n_1,\ldots,n_k}$ als ein mit wachsendem k immer feiner werdendes Gespinst, das den Raum überspannt, vorstellen, was den Namen Gewebe erklärt.

Gibt es in einem lokalkonvexen Raum ein solches Gewebe, so sagt man der Raum habe ein Gewebe oder sei ein Raum mit Gewebe. Der deutsche Begriff klingt ein wenig hölzern, die englische Bezeichnung webbed space lässt sich im Deutschen nicht so griffig wiedergeben.

Permanenzeigenschaften

Räume mit Gewebe haben sehr umfangreiche Permanenzeigenschaften:

• Ist E ein Raum mit Gewebe und 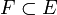$F\subset E$ ein abgeschlossener Unterraum, so sind auch F und der Quotientenraum E / F Räume mit Gewebe.
• Ist (E_n)_n eine Folge von lokalkonvexen Räumen mit Gewebe, so ist das direkte Produkt 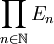$\prod_{n\in{\mathbb N}}E_n$ mit der Produkttopologie ein Raum mit Gewebe.
• Ist (E_n)_n eine Folge von lokalkonvexen Räumen mit Gewebe, so ist die direkte Summe 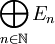$\bigoplus_{n\in{\mathbb N}}E_n$ mit der Finaltopologie ein Raum mit Gewebe.

Beispiele

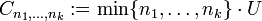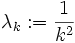• Banachräume E haben ein Gewebe. Ist nämlich U die Einheitskugel, so bilden die Daten $C_{n_1,\ldots,n_k} := \min\{n_1,\ldots,n_k\}\cdot U$ und $\lambda_k:=\frac{1}{k^2}$ (unabhängig von der Folge (n_k)_k!) ein Gewebe.

• Da jeder Fréchet-Raum ein abgeschlossener Unterraum eines abzählbaren direkten Produktes von Banachräumen ist, ergibt sich aus obigen Permanenzeigenschaften, dass Fréchet-Räume ein Gewebe haben.

• Weiter ergibt sich aus obigen Permanenzeigenschaften, dass abzählbare induktive Limiten von Fréchet-Räumen ein Gewebe haben, denn diese treten als Quotient abzählbarer direkter Summen von Frécheträumen auf. Insbesondere haben LF-Räume ein Gewebe.

• Folgenvollständige (DF)-Räume sind Räume mit Gewebe.

Graphensatz und Offenheit

Für lineare Operatoren zwischen Räumen mit Gewebe und ultrabornologischen Räumen kann man den Satz vom abgeschlossenen Graphen und den Satz von der offenen Abbildung beweisen. Man beachte bei den folgenden Sätzen die wechselnden Rollen der beteiligten Raumklassen:

Satz über die offene Abbildung: Sei E ein Raum mit Gewebe, F sei ultrabornologisch und 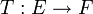$T:E\rightarrow F$ sei linear, stetig und surjektiv. Dann ist T offen.

Satz vom abgeschlossenen Graphen: Sei E ultrabornologisch, F sei ein Raum mit Gewebe, 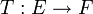$T:E\rightarrow F$ sei ein linearer Operator mit abgeschlossenem Graphen. Dann ist T stetig.

Quellen

• G. Köthe, Topological Vector Spaces II, Springer, 1979, ISBN 3-540-90400-X
• H. Jarchow: Locally Convex Spaces, Teubner, Stuttgart 1981 ISBN 3-519-02224-9
• R. Meise, D. Vogt: Einführung in die Funktionalanalysis, Vieweg, 1992 ISBN 3-528-07262-8