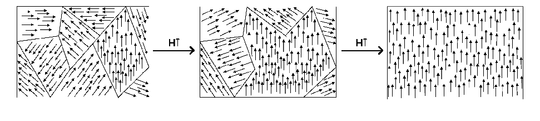
Weißsche Bezirke

Mehrere Körner von NdFeB. Innerhalb der Körner ist durch den hell/dunkel-Kontrast die Domänenstruktur erkennbar.

Als Weiss-Bezirke (auch weisssche Bezirke) bezeichnet man beim Magnetismus mikroskopisch kleine magnetisierte Domänen in den Kristallen eines ferromagnetischen Stoffes. Sie wurden benannt nach dem französischen Physiker Pierre-Ernest Weiss (1865–1940).

Weiss erkannte 1907, dass die magnetischen Momente der Atome („Elementarmagnete“) der Ferromagnetika auch ohne Einwirkung eines äußeren Feldes in begrenzten Bezirken parallel ausgerichtet sind. Die Größe dieser Bezirke erstreckt sich von etwa 10^-6 bis 10^-8 m linearer Ausdehnung, in denen sich etwa 10⁶ bis 10⁹ Atome befinden. Die Richtung der Magnetisierung orientiert sich an dem Kristallgitter des Werkstoffs. Bei Werkstoffen, deren Korngröße dieser Größenordnung entspricht oder noch darunter liegt, sind alle Kristallite Ein-Domänen-Teilchen, d. h. nicht weiter in Domänen unterteilt.

Von Natur aus sind die Weiss-Bezirke bis zur Sättigung magnetisiert. Die Grenzen zwischen den Bezirken heißen Bloch-Wände. Setzt man ein hartmagnetisches Material einem steigenden Magnetfeld aus, verschieben sich zunächst die Bloch-Wände zugunsten derjenigen Weiss-Bezirke, die in Richtung des äußeren Feldes ausgerichtet sind. Bei weiter steigendem äußeren Feld ändern schließlich immer mehr Weiss-Bezirke schlagartig ihre Polung (Barkhausen-Sprung). Dieses Umklappen kann man hörbar machen, indem man den Wechselanteil bzw. die stufenförmige Zunahme des magnetischen Feldes mit einer Spule induktiv aufnimmt und verstärkt. Bei Änderung des äußeren Feldes entsteht ein hysteresebehaftetes Rauschen, welches Rückschlüsse auf die magnetischen Eigenschaften des Materials zulässt.

Vergrößerung der Weiss-Bezirke durch die Ausrichtung mehrerer Domänen über ein externes magnetisches Feld

Weiss-Bezirke treten in Analogie dazu auch in Ferroelektrika auf; sie bilden bei diesen Bereiche einheitlicher Dipolausrichtung.

Literatur

• Hans Fischer: Werkstoffe in der Elektrotechnik. 2. Auflage, Carl Hanser Verlag, München Wien, 1982 ISBN 3-446-13553-7
• Horst Stöcker: Taschenbuch der Physik. 4. Auflage, Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4