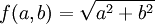Wertevorrat

Im Kontext einer mathematischen Funktion 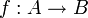$f : A \to B$, welche Elemente einer Menge A auf Elemente einer Menge B abbildet, bezeichnet man B als Zielmenge^[1] oder Wertevorrat^[2][3] der Funktion.

Häufig wird dafür auch das Wort Wertemenge^[4] oder Wertebereich^[3][5] benutzt; diese Wörter bezeichnen aber oft stattdessen die Bildmenge^[6] von f. Es besteht also Verwechslungsgefahr. Die Zielmenge ist nur der Vorrat für mögliche Werte von f – es ist nicht zwingend erforderlich, dass diese auch tatsächlich alle durch f angenommen werden.

Die Menge der Werte, die als Funktionswert von f erscheinen, ist die Bildmenge. Ist die Bildmenge von f gleich der Zielmenge von f, so heißt f surjektiv.

Die Zielmenge ist ein unterscheidender Bestandteil einer Funktion. Funktionen mit gleichem Definitionsbereich und gleicher Funktionsvorschrift, aber verschiedener Zielmenge, können niemals gleich sein.

Beispiel

Die Funktion 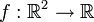$f : \mathbb{R}^2 \to \mathbb{R}$ ordne jedem Punkt der euklidischen Ebene seinen Abstand vom Nullpunkt zu. Es gilt also:

$f(a,b) = \sqrt{a^2+b^2}$

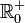Die Zielmenge der Funktion ist $\mathbb{R}$, die Menge der reellen Zahlen. Da der Abstand nie negativ sein kann, werden nicht alle möglichen Werte angenommen. Die Bildmenge besteht genau aus den nichtnegativen reellen Zahlen (oft mit $\mathbb{R}_0^+$ bezeichnet).

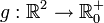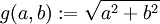Die Funktion $g : \mathbb{R}^2 \to \mathbb{R}_0^+$ mit $g(a,b) := \sqrt{a^2+b^2}$ hat denselben Definitionsbereich, dieselbe Funktionsvorschrift und dieselbe Bildmenge wie f. Da aber die Zielmengen verschieden sind, gilt trotzdem $f \ne g$.

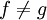Zusammenstellung der verschiedenen Mengen

Eine Funktion von A nach B.

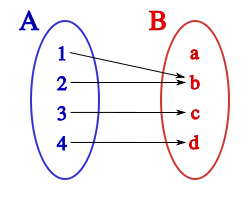
Anhand der nebenstehenden einfachen Beispielfunktion sollen noch einmal die verschiedenen auftretenden Mengen erklärt werden:

• Die Definitionsmenge (A) enthält die Elemente 1, 2, 3, 4.
• Die Zielmenge (B) enthält die Elemente a, b, c, d.
• Die Bildmenge besteht aus den Elementen b, c, d. Nur diese drei werden als Funktionswerte verwendet.
• Definitionsbereich ist ein anderes Wort für Definitionsmenge.
• Wertevorrat ist ein anderes Wort für Zielmenge.
• Wertemenge und Wertebereich sind in ihrer Bedeutung nicht eindeutig festgelegt und können die Zielmenge oder auch die Bildmenge bezeichnen.

Einzelnachweise

1. ↑ Harro Heuser, Lehrbuch der Analysis. Teil 1. 8. Auflage, B. G. Teubner, Stuttgart 1990. ISBN 3-519-12231-6. S 104
2. ↑ G. Wittstock Vorlesungsskript zu Analysis 1 Wintersemester 2000-2001. Bezeichnung 1.3.3, S. 19
3. ↑ ^{a b} Reinhard Dobbener: Analysis. Oldenbourg Wissenschaftsverlag 2007, ISBN 3486579991. S 12, Definition 1.12
4. ↑ Andreas Gathmann: Vorlesung Grundlagen der Mathematik (WS 2007/08 und SS 2008) Kapitel 1 Etwas Logik und Mengenlehre Seite 9, Definition 1.14
5. ↑ Michael Ruzicka: Analysis I. Vorlesung vom Wintersemester 2004/2005. S 21
6. ↑ Harro Heuser, Lehrbuch der Analysis. Teil 1. 8. Auflage, B. G. Teubner, Stuttgart 1990. ISBN 3-519-12231-6. S 106