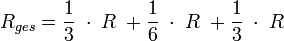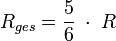Widerstandswürfel

Widerstandswürfel aus zwölf gleichen Widerständen

Unter dem Namen Widerstandswürfel ist eine skelettartige Drahtkonstruktion bekannt, dessen zwölf Kanten von zwölf in Würfelform miteinander verlöteten ohmschen Widerständen gebildet werden. Die Widerstände besitzen alle den gleichen Widerstandswert. Der Widerstandswürfel ist damit nicht nur optisch, sondern auch elektrisch symmetrisch aufgebaut. Wegen der unterschiedlichen räumlichen Position der Ecken zueinander, ergeben sich für die Ermittlung des Gesamtwiderstands drei verschiedene Varianten mit unterschiedlichen Ergebnissen, wobei sich die Widerstandsberechnung für die räumlich diagonal gegenüberliegenden Ecken hervorhebt, weil sich hier mehr Äquipotentialpunkte finden und somit die elektrische Symmetrie größer ist. Die Berechnung des Widerstandswürfels ist eine häufig gestellte Rechenaufgabe in der Ausbildung zu fachspezifischen Berufen.

Aufgabe

Zwölf gleichgroße ohmsche Widerstände befinden sich an den Kanten eines Würfels und sind leitend miteinander verbunden. Wie groß ist der Gesamtwiderstand an den räumlich diagonal gegenüberliegenden Ecken des Würfels? Hinweis: Bestimmen Sie zunächst alle Äquipotentialpunkte bezüglich der betreffenden Ecken unter Beachtung der gegebenen Symmetrie des Widerstandsnetzes.

Lösung

Würfel mit bezeichneten Ecken und eingezeichneten Diagonalen

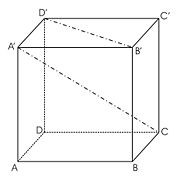
Der Widerstandswürfel wird mit zwölf gleichen Widerständen aufgebaut und ist deshalb auch elektrisch symmetrisch. Durch die drei an einer Ecke miteinander verbundenen Widerstände fließen wegen der Symmetrie beim Anlegen einer Spannung auch gleichgroße Ströme. Die der betrachteten Ecke abgewandten Enden dieser drei Widerstände liegen deshalb untereinander ebenfalls auf demselben Potential. Verbindet man Punkte gleichen Potentials, Äquipotentialpunkte, miteinander leitend, fließt über diese Verbindungen kein Strom in Ermangelung einer Spannung zwischen diesen. Daraus folgt, dass diese zusätzlichen Verbindungen die Schaltung nicht verändern. Ferner ist ersichtlich, dass durch die Widerstände der gleiche Strom fließen muss, da an ihnen dieselbe Spannung abfällt. So lassen sich am Widerstandswürfel bei der Ermittlung des Gesamtwiderstands über den Ecken der Raumdiagonalen (in der Grafik die Ecken A' und C) zwei mal drei potentialgleiche Punkte (in der Grafik die Punkte A, B', D' und B, C', D) finden, die ohne eine elektrische Veränderung zu verursachen, jeweils miteinander verbunden werden können. Nach dem Herstellen dieser Verbindungen ergibt sich die übersichtliche Reihenschaltung einer Parallelschaltung von drei Widerständen mit einer Parallelschaltung von sechs Widerständen und einer Parallelschaltung von drei Widerständen.

Rechnung

$R_{ges} = \frac{1}{3} \; \cdot \; R \; + \frac{1}{6} \; \cdot \; R \; + \frac{1}{3} \; \cdot \; R \;$

$R_{ges} = \frac{5}{6} \; \cdot \; R \;$

Weblinks

• PDF-Dokument der FH Aachen mit Informationen zum Widerstandswürfel