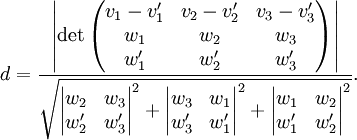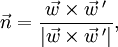Windschief

Darstellung zweier windschiefer Geraden

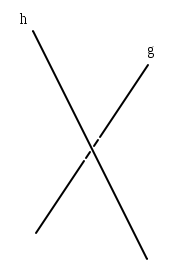
In der Geometrie nennt man zwei Geraden windschief oder einander kreuzend, wenn sie sich weder schneiden noch parallel zueinander sind. Dies ist erst im dreidimensionalen Raum möglich. Im n-dimensionalen Raum können (n-2)-dimensionale Objekte windschief sein.

Zur Begründung, dass zwei Geraden g und h windschief sind, genügt es zu zeigen, dass ein Richtungsvektor von g, ein Richtungsvektor von h und ein Verschiebungsvektor von einem Punkt auf g zu einem Punkt auf h linear unabhängig sind. Äquivalent kann man zeigen, dass es keine Ebene gibt, die beide Geraden enthält.

Abstand zweier windschiefer Geraden

Die eindeutig bestimmte Strecke kleinster Länge, die zwei windschiefe Geraden verbindet, nennt man Gemeinlot oder Minimaltransversale. Sie ist auch die einzige Strecke, die senkrecht auf beiden Geraden steht. Die Länge dieser Strecke ist der Abstand der Geraden.

Zur Berechnung des Abstandes kann man durch die eine Gerade eine Ebene legen, die zu der anderen Geraden parallel ist. Der Abstand der beiden Geraden zueinander ist identisch mit dem eines beliebigen Punktes der anderen Geraden zur konstruierten Ebene.

Für die windschiefen Geraden g, h mit der Parameterdarstellung

$g = \{ \vec v + t\,\vec w \mid t \in \R \}$

$h = \{ \vec v\,' + t\,\vec w\,' \mid t \in \R \}$ ,

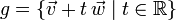
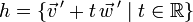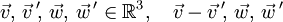$\vec v,\,\vec v\,'\!,\,\vec w,\,\vec w\,' \in \R^3, \quad \vec v - \vec v\,'\!,\,\vec w,\,\vec w\,'$  linear unabhängig

beträgt er

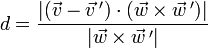$d = \frac{|(\vec v - \vec v\,') \cdot (\vec w \times \vec w\,')|}{|\vec w \times \vec w\,'|}$   (siehe Skalarprodukt und Kreuzprodukt).

Mit Koordinaten geschrieben

$g = \left\{ \left(\begin{smallmatrix} v_1 \\[0.7ex] v_2 \\[0.7ex] v_3 \end{smallmatrix}\right) + t \left(\begin{smallmatrix} w_1 \\[0.7ex] w_2 \\[0.7ex] w_3 \end{smallmatrix}\right) \bigg|\,t \in \R \right\}$   und   $h = \left\{ \left(\begin{smallmatrix} v_1' \\ v_2' \\ v_3' \end{smallmatrix}\right) + t \left(\begin{smallmatrix} w_1' \\ w_2' \\ w_3' \end{smallmatrix}\right) \bigg|\,t \in \R \right\}$

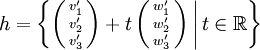
ergibt das mit der Determinante det die Formel

$d = \frac{\left| \det \begin{pmatrix} v_1-v_1' & v_2-v_2' & v_3-v_3' \\ w_1 & w_2 & w_3 \\ w_1' & w_2' & w_3' \end{pmatrix}\right|}{\sqrt{\begin{vmatrix} w_2 & w_3 \\ w_2' & w_3'\end{vmatrix}^2 + \begin{vmatrix} w_3 & w_1 \\ w_3' & w_1'\end{vmatrix}^2 + \begin{vmatrix} w_1 & w_2 \\ w_1' & w_2'\end{vmatrix}^2}}.$

Begründung der Formel

Das Gemeinlot, zu beiden Geraden senkrecht, ist ein Normalenvektor der Ebene, da sie g enthält und zu h parallel ist. Einen solchen Normalenvektor $\vec n$ erhält man über das Kreuzprodukt der beiden Richtungsvektoren,

$\vec n = \frac{\vec w \times \vec w\,'}{|\vec w \times \vec w\,'|},$

hier durch den Nenner auf Länge Eins normiert.

Damit lautet obige Formel

$d = |(\vec v - \vec v\,') \cdot \vec n|$.

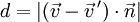Es handelt sich also um die Länge der Projektion des Differenzvektors 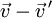$\vec v - \vec v\,'$ auf die geforderte Richtung.

Für die Berechnung des Abstands der Geraden g von h ist es also weder nötig, eine Darstellung der Ebene E anzugeben, noch die Koordinaten der durch das Gemeinlot verbundenen Punkte Q auf g und Q' auf h auszurechnen. Q findet man als Schnittpunkt der um d entlang $\vec n$ verschobenen Geraden h mit g.

Weblinks