WxMaxima

Maxima
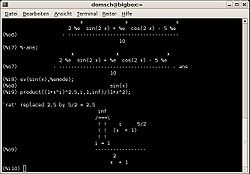
Screenshot von Maxima in einer Shell
Basisdaten
Aktuelle Version:	5.17.1 (15. Dezember 2008)
Betriebssystem:	Plattformunabhängig
Kategorie:	Computeralgebrasystem
Lizenz:	GPL
maxima.sourceforge.net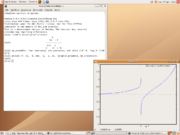

Maximas Funktionsplotter auf Basis von Gnuplot

Maxima ist ein Computeralgebrasystem, das als Open-Source-Projekt unter der GNU General Public License (GPL) entwickelt wird.

Implementiert ist Maxima in Common Lisp. Es existieren Versionen für Windows, Mac OS X und Linux.

Geschichte

Maxima ist eine Version von Macsyma, einem der ersten Computeralgebrasysteme. Es wurde in den 1960er Jahren im Auftrag des US-Energieministeriums (DOE) am MIT entwickelt. Eine Macsyma-Version (DOE Macsyma) wurde von William Schelter von 1982 bis zu seinem Tod 2001 weiterentwickelt. 1998 erhielt Schelter vom Energieministerium die Genehmigung, seine Version unter der GPL zu veröffentlichen^[1]. Diese Version wird nun unter dem Namen Maxima von einer unabhängigen Gruppe von Anwendern und Entwicklern gepflegt.^[2][3]

Maxima Frontends

wxMaxima

wxMaxima

Mit dem Programm wxMaxima ist darüber hinaus eine auf wxWidgets basierende grafische Benutzeroberfläche für Maxima verfügbar, die durch Menüs und Dialoge die Nutzung des Programms vereinfacht und eine grafische Formelausgabe besitzt. Ab Version 5.10.0b ist die aktuelle Version von wxMaxima bereits im Installationspaket für Windows integriert.

Emacs: maxima.el und imaxima

Der Emacs-Editor enthält mit maxima.el ebenfalls ein Frontend für Maxima. maxima.el leitet die Ausgabe von Maxima in einen Emacs-Buffer um. Mit imaxima gibt es eine Erweiterung, die die Ausgabe von maxima mittels LaTeX im Emacs-Buffer darstellt.

Fähigkeiten

Maxima enthält eine ALGOL-ähnliche Programmiersprache mit LISP-Semantik und kann unter anderem folgende Aufgabenklassen symbolisch und numerisch (mit frei wählbarer Stellengenauigkeit) lösen:

• Manipulation von algebraischen Ausdrücken mit reellen oder komplexen Konstanten, Variablen und Funktionen
• Grenzwerte ermitteln
• Gleichungen lösen
• Polynome faktorisieren und lösen
• Differenzieren mit wählbarem Grad
• Funktionen in Taylorreihen oder Potenzreihen entwickeln
• Laplace-Transformation
• Integrieren (unter Umständen müssen geeignete Substitutionen vorgenommen werden)
• Lösen von gewöhnlichen Differentialgleichungen 1. und 2. Ordnung
• Lösen von Anfangs- und Randwertaufgaben
• Padé-Approximation von Funktionen
• Lineare Algebra: Inverse Matrix, Eigenwerte, Eigenvektoren, charakteristisches Polynom berechnen.

Weitere Fähigkeiten

• Funktionsplotter (auf Basis von Gnuplot und OpenMath)
• TeX-Ausgabe
• HTML-Ausgabe
• Compiler, um Maxima-Ausdrücke in Fortran-Code umzuwandeln

Weblinks

• Webseite von Maxima (englisch)
• Webseite von wxMaxima (englisch)
• Webseite von iMaxima (englisch)
• irc://irc.freenode.net#maxima - IRC-Channel
• Deutschsprachiges Online-Tutorial - Austromath Bildungsserver

Einzelnachweise

1. ↑ http://maxima.sourceforge.net/authorization-letter.html
2. ↑ http://maxima.sourceforge.net/wiki/index.php/History%20and%20other%20context
3. ↑ http://maxima.sourceforge.net/wiki/index.php/General