- Z(G)
-
Im mathematischen Teilgebiet der Algebra bezeichnet das Zentrum einer Algebra oder einer Gruppe diejenige Teilmenge der betrachteten Struktur, die aus all denen Elementen besteht, die mit allen Elementen bzgl. der Multiplikation kommutieren.
Inhaltsverzeichnis
Zentrum einer Gruppe
Ist G eine Gruppe, so ist deren Zentrum die Menge
Das Zentrum von G ist eine Untergruppe, denn sind x und y aus Z(G), dann gilt für jedes g aus G
- (xy)g = x(yg) = x(gy) = (xg)y = (gx)y = g(xy),
also liegt auch xy im Zentrum. Analog zeigt man, dass x − 1 im Zentrum liegt. Das neutrale Element der Gruppe liegt stets im Zentrum.
Eigenschaften
Das Zentrum ist abelsch und ein Normalteiler von G, es ist sogar eine charakteristische Untergruppe von G. Ist G selbst abelsch, dann ist Z(G) = G.
Das Zentrum besteht aus genau den Elementen z von G, für die die Konjugation mit z
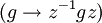 die identische Abbildung ist.
die identische Abbildung ist.Beispiele
- Das Zentrum der symmetrischen Gruppe S3 = {id, (1,2), (1,3), (2,3), (1,2,3), (1,3,2)} besteht nur aus dem neutralen Element id, denn:
- (1,2)(1,3) = (1,3,2) ≠ (1,3)(1,2) = (1,2,3)
- (1,2)(2,3) = (1,2,3) ≠ (2,3)(1,2) = (1,3,2)
- (1,2,3)(1,2) = (1,3) ≠ (1,2)(1,2,3) = (2,3)
- (1,3,2)(1,2) = (2,3) ≠ (1,2)(1,3,2) = (1,3)
- Die Diedergruppe D8 besteht aus den Bewegungen der Ebene, die ein fest gewähltes Quadrat unverändert lassen. Es sind dies die Drehungen um den Mittelpunkt des Quadrats um Winkel von 0°, 90°, 180° und 270°, sowie vier Spiegelungen an den beiden Diagonalen und den beiden Mittelparallelen des Quadrats. Das Zentrum dieser Gruppe besteht genau aus den beiden Drehungen um 0° und um 180°.
- Das Zentrum der multiplikativen Gruppe der invertierbaren n×n-Matrizen mit Einträgen in den reellen Zahlen besteht aus den reellen Vielfachen der Einheitsmatrix.
Zentrum eines Rings
Das Zentrum eines Rings R besteht aus denjenigen Elementen des Rings, die mit allen anderen kommutieren:
Das Zentrum Z(R) ist ein kommutativer Unterring von R. Ein Ring stimmt genau dann mit seinem Zentrum überein, wenn er kommutativ ist.
Zentrum einer assoziativen Algebra
Das Zentrum einer assoziativen Algebra A ist die kommutative Unteralgebra
Eine Algebra stimmt genau dann mit ihrem Zentrum überein, wenn sie kommutativ ist.
Zentrum einer Liealgebra
Das Zentrum einer Liealgebra
 ist das (abelsche) Ideal
ist das (abelsche) IdealEine Liealgebra stimmt genau dann mit ihrem Zentrum überein, wenn sie abelsch ist.
Beispiel
- Das Zentrum von
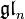 besteht aus den skalaren Vielfachen der Einheitsmatrix.
besteht aus den skalaren Vielfachen der Einheitsmatrix. - Für eine assoziative Algebra mit dem Kommutator als Lieklammer stimmen die beiden Zentrumsbegriffe überein.
Literatur
- Kurt Meyberg: Algebra - Teil 1. Hanser 1980, ISBN 3-446-13079-9, S. 36
Weblinks
Wikimedia Foundation.

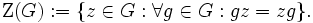
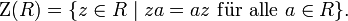
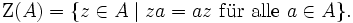
![\mathfrak z(\mathfrak g)=\{Z\in \mathfrak g\mid[X,Z]=0\ \mathrm{f\ddot ur\ alle}\ X\in\mathfrak g\}.](/pictures/dewiki/57/934900cac9dde7303c1a4e917206cc4a.png)