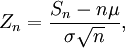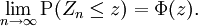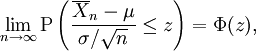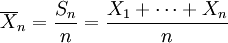ZGWS

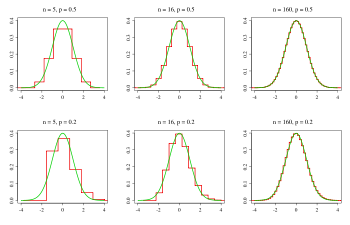Annäherung von geraden (oben) und schiefen (unten) Binomialverteilungen (rot) an die Normalverteilung (grün)

Bei den Zentralen Grenzwertsätzen handelt es sich um eine Familie schwacher Konvergenzaussagen aus der Wahrscheinlichkeitstheorie. Allen gemeinsam ist die Aussage, dass die (normierte und zentrierte) Summe einer großen Zahl von unabhängigen, identisch verteilten Zufallsvariablen annähernd (standard)normalverteilt ist. Dies erklärt auch die Sonderstellung der Normalverteilung.

Die wichtigste und bekannteste Aussage wird auch einfach als Der Zentrale Grenzwertsatz bezeichnet und befasst sich mit unabhängigen, identisch verteilten Zufallsvariablen, deren Erwartungswert und Varianz endlich sind.

Es existieren verschiedene Verallgemeinerungen, für die eine identische Verteilung keine notwendige Voraussetzung ist. Stattdessen wird dann eine andere Voraussetzung gefordert, die sicherstellt, dass keine der Variablen zu großen Einfluss auf das Ergebnis erhält. Beispiele sind die Lindeberg-Bedingung und die Ljapunow-Bedingung. Darüber hinausgehende Verallgemeinerungen gestatten sogar „schwache“ Abhängigkeit der Zufallsvariablen.

Der Zentrale Grenzwertsatz der Statistik bei identischer Verteilung

(auch bekannt als Grenzwertsatz von Lindeberg / Levy)

Sei 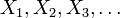$X_1, X_2, X_3, \dots$ eine Folge von Zufallsvariablen, die auf demselben Wahrscheinlichkeitsraum alle dieselbe Verteilung D aufweisen und unabhängig sind (u.i.v., unabhängig und identisch verteilt; engl. i.i.d., independent and identically distributed). Sei weiter angenommen, dass sowohl der Erwartungswert μ als auch die Standardabweichung σ existieren und endlich sind.

Betrachten wir nun die n-te Teilsumme dieser Zufallsvariablen $S_n = X_1 + X_2 +\cdots + X_n$. Der Erwartungswert von S_n ist nμ und die Varianz ist nσ². Bildet man daraus die standardisierte Zufallsvariable

$Z_n = \frac{S_n - n \mu}{\sigma \sqrt{n}},$

dann besagt der Zentrale Grenzwertsatz, dass die Verteilung von Z_n für n →$\infty$ gegen die Standardnormalverteilung N(0,1) konvergiert. Ist Φ(z) die Verteilungsfunktion von N(0,1), dann bedeutet dies, dass für jedes reelle z

$\lim_{n \to \infty} \mbox{P}(Z_n \le z) = \Phi(z).$

In etwas anderer Schreibweise erhält man

$\lim_{n\rightarrow\infty}\mbox{P}\left(\frac{\overline{X}_n-\mu}{\sigma/\sqrt{n}}\leq z\right)=\Phi(z),$

wobei

$\overline{X}_n=\frac {S_n} n=\frac {X_1+\cdots+X_n} n$

der Mittelwert der ersten n Summanden der Zufallsvariablen ist.

Existiert das dritte zentrierte Moment 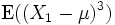$\operatorname{E}((X_1-\mu)^3)$ und ist es endlich, dann ist diese Konvergenz sogar gleichmäßig und die Konvergenzgeschwindigkeit ist wenigstens von der Ordnung $\frac 1 {\sqrt {n}}$ (Satz von Berry-Esseen).

Handelt es sich bei der Verteilung D um die Binomialverteilung, dann gelangt man zu einem Spezialfall des zentralen Grenzwertsatzes, der als Satz von Moivre-Laplace bekannt ist.

Trivia

Durch die außergewöhnliche Bedeutung des zentralen Grenzwertsatzes für die gesamte Statistik und da in diesem standardisierte Zufallsvariablen verwendet werden, werden diese in Anlehnung an den Anfangsbuchstaben dieses Satzes meist mit einem Z bezeichnet und der Vorgang des Standardisierens als z-Transformation bezeichnet.

Siehe auch

• Tabelle Standardnormalverteilung

Weblinks

• Beispiel zur Verdeutlichung des Zentralen Grenzwertsatzes
• Ein graphisches Beispiel zur Addition von nicht normal und verschieden verteilten Zufallsvariablen
• Interaktives Experiment zum Zentralen Grenzwertsatz