Zero-Knowledge

Ein Zero-Knowledge-Beweis oder Zero-Knowledge-Protokoll ist ein Protokoll aus dem Bereich der Kryptografie. Bei einem Zero-Knowledge-Protokoll kommunizieren zwei Parteien (der Beweiser und der Verifizierer) miteinander. Der Beweiser überzeugt dabei den Verifizierer mit einer gewissen Wahrscheinlichkeit davon, dass er ein Geheimnis kennt, ohne dabei Informationen über das Geheimnis selbst bekannt zu geben.

Ein bekanntes Verfahren ist das Feige-Fiat-Shamir-Protokoll.

Zero-Knowledge-Protokolle dienen u.a. der Authentifizierung. In der Praxis werden sie jedoch kaum verwendet, da sie in der Regel für ein ausreichendes Sicherheitsniveau ein hohes Maß an Interaktion, d.h. den Austausch vieler Nachrichten, erfordern. Die in praktischen Anwendungen eingesetzten und standardisierten Authentifizierungsprotokolle basieren stattdessen auf digitalen Signaturen. Allerdings gibt es auch Konstruktionen, welche bestimmte Zero-Knowledge Protokolle in nicht-interaktive Varianten überführen.

Zero-Knowledge-Protokolle stellen eine Erweiterung von interaktiven Beweissystemen dar. Zu den Bedingungen Vollständigkeit und Zuverlässigkeit der interaktiven Beweissysteme tritt noch die Zero-Knowledge-Eigenschaft, die dafür sorgt, dass der Verifizierer keine Information über das Geheimnis erlangt.

Bei einem Zero-Knowledge-Protokoll soll immer gezeigt werden, dass eine Eingabe x einer formalen Sprache L angehört. Dazu muss ein Zero-Knowledge-Protokoll drei Bedingungen erfüllen:

Vollständigkeit

Ist die Eingabe x ein Element der Sprache L, dann soll ein Verifizierer nach Ablauf des Protokolls fast immer akzeptieren.

Zuverlässigkeit

Ist die Eingabe x kein Element der Sprache L, also der Beweiser unehrlich, dann soll der Verifizierer nach Ablauf des Protokolls ablehnen. Dabei ist jedoch eine geringe Fehlerwahrscheinlichkeit erlaubt.

Zero-Knowledge-Eigenschaft

Aus der Interaktion zwischen dem Beweiser und dem Verifizierer darf nicht mehr Wissen als die (Un-)Gültigkeit der zu beweisenden Aussage gewonnen werden.

Historischer Zero-Knowledge-Beweis

Im 16. Jahrhundert bewies Niccolo Fontana Tartaglia, im Besitz der Lösungsformel für Gleichungen dritten Grades zu sein, indem er deren Nullstellen berechnete. Er musste die Lösungsformel selbst nicht publizieren, da er die Nullstellen berechnen konnte und dadurch darauf geschlossen werden konnte, dass er im Besitz eines Lösungsweges sein musste.

Anmerkung: Der Verifizierer erlangt neues Wissen (die Lösung). Streng genommen dürfte das nicht passieren. Denn damit könnte er Andere ebenfalls davon überzeugen, dass er oder Tartaglia diese Lösungsformel kennt. Deswegen kann man Niccolo Fontana Tartaglia vermutlich nicht als den "Erfinder" von Zero-Knowledge-Beweisen sehen.

Beispiel für ein Zero-Knowledge-Protokoll

Ein Zero-Knowledge-Protokoll mit ISOGRAPH

Eine Zero-Knowledge-Authentifizierung zwischen zwei Instanzen kann mit Hilfe des Graphenisomorphieproblems stattfinden. Dazu muss vom Beweiser zunächst einmalig ein öffentliches Schlüsselpaar erstellt werden:

• Der Beweiser B erzeugt einen sehr großen Graphen G₀.
• B nummeriert G₀ mit einer zufällig und gleichförmig gewählten Permutationsfunktion π um. Der resultierende Graph sei also G₁: = π(G₀).
• Das Paar (G₀,G₁) wird veröffentlicht, die Permutation π hält B geheim.

Angenommen, eine Person, genannt "Verifizierer", möchte die Identität von B überprüfen, d.h. feststellen, ob B tatsächlich im Besitz des zum öffentlichen Schlüssel (G₀,G₁) gehörigen privaten Schlüssels π ist. Dann kann B diese Tatsache mit Hilfe des nachfolgenden Zero-Knowledge-Protokolls beweisen, ohne dem Verifizierer oder einer dritten Person den privaten Schlüssel π mitzuteilen:

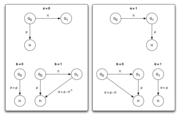
1. Der Beweiser B wählt zufällig ein 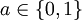$a \in \{0,1\}$. Außerdem wird der Graph G_a durch die zufällig gewählte Permutationsfunktion ρ umnummeriert. Der resultierende Graph sei H: = ρ(G_a). B sendet schließlich H an den Verifizierer V. In diesem Schritt legt sich der Beweiser also auf einen der Graphen fest (Commitment bzw. Witness).
2. Der Verifizierer V empfängt den Graphen H und wählt zufällig ein 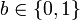$b \in \{0,1\}$. Dann fordert er B auf, ihm eine Permutation σ mit der Eigenschaft H = σ(G_b) zu senden (Challenge).
3. Nun muss zwischen drei Fällen unterschieden werden:

   $\sigma := \begin{cases} \rho & \mbox{falls } a=b\\ \rho \circ \pi^{-1} & \mbox{falls } a=0\ \mbox{und }b=1\\ \rho \circ \pi & \mbox{falls } a=1\ \mbox{und }b=0 \end{cases}$

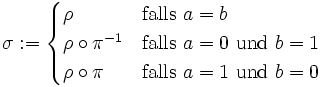
   B schickt die entsprechend konstruierte Permutation σ an V zurück (Response).

4. V empfängt das von B gesendete σ und prüft ob wirklich H = σ(G_b) gilt.

Wir betrachten nun die drei notwendigen Bedingungen für ein Zero-Knowledge Protokoll:

• Das obige Protokoll ist offensichtlich vollständig, weil σ gerade so konstruiert wird, dass es die geforderte Gleichung H = σ(G_b) erfüllt.
• Ein unehrlicher Beweiser bzw. eine dritte Person, die sich als B ausgeben möchte, kann ohne Kenntnis von π den Verifizierer nur mit einer Wahrscheinlichkeit von 0,5 (durch richtiges Raten des Wertes b im ersten Schritt) überzeugen. Falls das Protokoll hinreichend oft wiederholt wird und unter der Annahme, dass die Bestimmung von π aus (G₀,G₁) schwer ist, ist das Protokoll also zuverlässig.
• Die Kommunikation zwischen Beweiser und Verifizierer in einer Runde (Schritt 1 bis 4) ist von der Form (H,b,σ). Erzeugt nun ein Simulator S zufällig und gleichförmig b' und σ' und berechnet damit den Graphen H' = σ'(G_b'), dann ist die resultierende Wahrscheinlichkeitsverteilung {(H',b',σ')} identisch mit der Verteilung, welche durch die echten Protokollinstanzen impliziert wird. Folglich kann kein geheimes Wissen (hier die Permutation π) übertragen worden sein (Zero-Knowledge).

Literatur

• Jean-Jacques Quisquater, Louis Guillou: How to explain zero-knowledge protocols to your children. Advances in Cryptology - CRYPTO '89, Lecture Notes in Computer Science 435, pp. 628-631, 1990. [1]

  Kommentar: Äußerst unterhaltsame und theoriearme Einführung anhand eines mittlerweile klassischen Beispiels.

Weblinks

• Applied Kid Cryptography – Eine sehr anschauliche Darstellung eines Zero-Knowledge Protokolls anhand eines Spiels.
• Zero-Knowledge Tutorial – Hervorragende Einführung von Oded Goldreich (in Englisch)