Zinsstrukturkurve

Die USD-Zinsstruktur von 2000-2006: Deutlich ist zu sehen, dass die kurzfristigen Zinsen im Laufe der letzten Jahre gestiegen sind, während die langfristigen Zinsen nahezu konstant geblieben sind. Zur Zeit ist die Zinssturktur flach bis teilweise schon invers.

Beispiele für normale (1973), flache (1990), inverse (1991) und aktuelle Zinskurven

Vier verschienede Beschreibungen der Zinsstruktur; hier ausgehend von den Swap Raten

Als Zinsstruktur bezeichnet man das Verhältnis verschiedener Zinssätze zueinander. Der jeweilige Zinssatz hängt im Allgemeinen von der Laufzeit, dem Risiko, der steuerlichen Behandlung und sonstigen Eigenschaften der entsprechenden Finanzinstrumente ab. Im Folgenden wird die zeitliche Zinsstruktur betrachtet, bei der die Abhängigkeit des Zinssatzes von der Bindungsdauer einer Anlage (Verzinsliches Wertpapier) im Vordergrund steht.

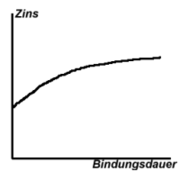
Typischerweise erhält ein Anleger für Geld, das für einen langfristigen Zeitraum fest angelegt wird, einen höheren Zinssatz als für Geld, das nur kurzfristig angelegt wird — der Zinssatz steigt also mit der Bindungsdauer. Eine solche Zinsstruktur wird deshalb als steigend (bzw. normal) bezeichnet.

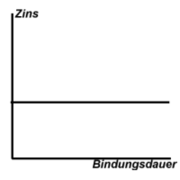
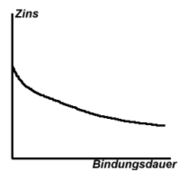
Die Zinsstruktur wird als flach bezeichnet, wenn der Zinssatz von der Bindungsdauer unabhängig ist. Dies ist jedoch die Ausnahme. Selten sind inverse (bzw. fallende) Zinsstrukturen. Sie treten auf, wenn für langlaufende Titel (Anleihe) weniger Zinsen bezahlt werden als für kurzfristige Titel.

Die Zinsstruktur wird grafisch in der so genannten Zinskurve (auch Zinsstrukturkurve) veranschaulicht. Mit kurzem Ende bezeichnet man die Laufzeit bis zu einem Jahr und mit dem langen Ende die Laufzeit ab circa fünf Jahren bis zu zehn Jahren in Deutschland und bis zu dreißig Jahren in den USA. Ein ähnlicher Indikator ist der Zinsspread.

Bedeutung

Die Zinsstruktur hat für Wirtschaftsforscher eine große Bedeutung zur Abschätzung der zukünftigen Entwicklung der Finanzmärkte und der Wirtschaft. Portfolio-Manager, die z. B. für Versicherungen oder Pensionskassen Geld anlegen, schätzen damit Risiken und Anlagestrategien ab. Außerdem sind auf den Kapitalmärkten weltweit sehr große Summen in festverzinslichen Wertpapieren angelegt, von Zinsänderungen sind also große Kapitalmengen betroffen.

Erklärungsmodelle für die Zinsstruktur

Es gibt drei Erklärungsmodelle, warum die Höhe des Zinssatzes von der Bindungsdauer abhängig ist. Diese drei Zinsstrukturhypothesen ergänzen sich teilweise, teilweise konkurrieren sie miteinander.

Die (reine) Erwartungshypothese

Die reine Erwartungshypothese folgt aus der Annahme der vollständigen Informationseffizienz des Marktes und der Annahme der vollständigen Risikoneutralität der am Markt handelnden Subjekte.

Daraus ergibt sich folgendes Bild:

• Werden steigende Zinsen am Markt erwartet, so investieren die Anleger vorzugsweise in "Kurzläufer", d. h. die Nachfrage am sog. kurzen Ende der Zinskurve steigt. Dies schmälert folglich die Renditen für Titel kurzer Laufzeit und die Zinskurve steigt (normale Zinsstruktur).
• Werden am Markt fallende Zinsen erwartet, so tritt das Gegenteil ein: Anleger wollen ihr Kapital lieber langfristig zu höheren Zinssätzen anlegen. Durch das Zusammenspiel von Angebot und Nachfrage entwickelt sich dann die inverse Zinsstruktur, zu der es oft vor Rezessionen kommen kann.

Die Erwartungshypothese liefert die gedankliche Grundlage für die Berechnung von forward rates bzw. impliziten Terminzinssätze die den erwarteten Spotzinssätzen entsprechen.

Seit Fama ist bekannt, dass Forward Rates die Richtung, aber nicht das Ausmaß von Zinsänderungen prognostizieren.

Die Erwartungshypothese erklärt, warum in Hochzinsphasen die Zinsstruktur häufig invers ist und warum in Niedrigzinsphasen die Zinsstruktur in der Regel steigend ist. Sie erklärt jedoch nicht, warum steigende Zinsstrukturen die Regel und inverse Zinsstrukturen die Ausnahme sind. Darüber hinaus vernachlässigt sie, dass langlaufende Anlagen ein höheres Risiko aufweisen als kurzfristige.

Die Liquiditätspräferenzhypothese

Die Liquiditätspräferenzhypothese ergänzt zur Erwartungshypothese den Umstand, dass Investoren ihre zukünftigen Pläne nicht genau kennen und deshalb ihre Mittel lieber kurzfristig anlegen. Dies wird durch die Furcht begründet, dass man langfristig angelegte Mittel nur zu ungünstigen Bedingungen wieder flüssig machen kann.

Um die Investoren zu langfristigen Anlagen zu motivieren, wird daher eine Liquiditätsprämie bezahlt. Dies erklärt, warum die Zinsstruktur in aller Regel steigend ist. Kombiniert man die Aussagen von Erwartungshypothese und Liquiditätspräferenzhypothese, so kann man aus der Zinsstruktur die vom Markt erwartete Zinsänderung ableiten, zum Beispiel:

• Eine schwach steigende Zinsstruktur bedeutet somit, dass für langlaufende Titel lediglich die Liquiditätsprämie bezahlt wird und der Markt somit keine Zinsänderung erwartet.
• Eine stark steigende Zinsstruktur bedeutet, dass der Markt steigende Zinsen erwartet: Es wird für langlaufende Titel im Vergleich zu kurzfristigen Bindungen mehr als die Liquiditätsprämie gezahlt.

Die Liquiditätspräferenzhypothese allein kann inverse Zinsstrukturkurven nicht erklären.

Die Marktsegmentierungshypothese

Die Marktsegmentierungshypothese beruht auf der Erfahrung, dass es keinen einzigen einheitlichen Anlagemarkt gibt, sondern dass die Marktteilnehmer in einem Segment operieren und dieses selten verlassen. Somit gibt es Angebot/Nachfrage-Situationen in jedem einzelnen Segment, was zu verschiedenen Zinssätzen in den einzelnen Segmenten und damit einer nicht-flachen Zinsstruktur führt. Ferner wird davon ausgegangen, dass auf Grund mangelnder Voraussicht und der daraus begründeten Risikoaversion das Marktverhalten der Kreditgeber durch Liquiditätspräferenz charakterisiert ist. Dies erklärt den überwiegend normalen Verlauf der Zinsstrukturkurve. Der Einfluss von Erwartungen über die Entwicklung der Zinsen auf die Zinsstrukturkurve schließt die Marktsegmentierungshypothese grundsätzlich aus.

Damit ist die Marktsegmentierungshypothese in der Lage zu erklären, warum es auch (aber selten) zu unregelmäßigen Zinsstrukturen kommt, z.B. mit einem Buckel. Eine Erklärung, warum inverse Zinsstrukturkurven häufiger bei hohen kurzfristigen Zinssätzen auftreten, kann das Modell jedoch nicht geben. Aus den Modellannahmen folgt zudem, dass Wertpapiere unterschiedlicher Laufzeiten intrasegmental nicht substituierbar sind.

Neben diesen Zinsstrukturtheorien bzw. -hypothesen, die den Verlauf der Zinsstruktur durch Faktoren erklären wollen, die im Grunde außerhalb der Finanzmärkte liegen (Erwartungen, Präferenz für möglichst liquides Vermögen und feststehende, meistens institutionell bestimmte Bevorzugung ganz bestimmter Laufzeiten), gibt es die sogenannten Zinsstrukturmodelle im engeren Sinne. Diese haben den viel bescheideneren Anspruch, die Zusammenhänge innerhalb der Zinsstrukturkurve, das heißt die Zusammenhänge zwischen Zinssätzen unterschiedlicher Restlaufzeiten zu erklären.

Spot rates und forward rates

Die Zinsstruktur ist eine Abfolge von spot rates, das heißt, von Zinssätzen gültig ab dem heutigen Tag, zu ihrer Bindungsdauer.

Aus der Zinsstruktur können forward rates berechnet werden, das sind Zinssätze, die ab einem bestimmten Datum in der Zukunft zu einer bestimmten Bindungsdauer gelten.

Ermittlung der Zinsstruktur

Eine wichtige Quelle für Rohdaten sind hier die Renditen von erstklassigen Nullkuponanleihen mit verschiedenen Restlaufzeiten, aber auch Kuponanleihen, z.B. die Preise von Staatsanleihen, werden genutzt. Die kupontragenden Anleihen bringen das Problem der Kuponverzerrung (Der Kupon hat eine andere Laufzeit als die gesamte Anleihe) mit sich. Daher ist die Berechnung sehr schwierig. Grundsätzlich müssen natürlich alle anderen Variablen, wie z. B. die Bonität des Schuldners, konstant sein. Gegebenenfalls wird die Zinsstrukturkurve durch die Sätze der Swapmärkte oder Marktzinssätze (LIBOR, …) ermittelt.

Swapmärkte

Hier wird sich zu Nutze gemacht, dass Swapsätze identisch sind mit Kupons von Anleihen, die zu pari notieren. Es verursacht jedoch auch Sonderprobleme.

Auf unvollkommenen Märkten kann die Wahl des Referenzzinssatzes die Bewertungszinssätze beeinflussen. Es ergeben sich Dispositionserträge durch die Ausnutzung kurzfristiger Preisdifferenzen.

Problem:

Die ermittelten Zero-Bond-Renditen beziehen sich auf den Swapmarkt und sind nicht mit den Bundesanleihen vergleichbar, da sie empirisch 30 bis 40 Basispunkte höher liegen.

Bootstrapping

Um aus der Swap-/Renditekurve die Zinskurve zu berechnen, wird das sogenannte Bootstrapping benutzt. Dabei werden die Diskontfaktoren sukzessive aus den Faktoren der vorhergehenden Perioden berechnet.

Da für einen Zero Bond gilt: $100 = cf_n\cdot df_1+cf_n\cdot df_2+ \cdots +(100+cf_n)\cdot df_n$

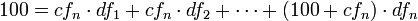
folgt für den Diskontfaktor des Jahres $\ n$: $df_n = \frac{100-\sum_{i=1}^{n-1} cf_n\cdot df_i}{100+cf_n}$

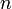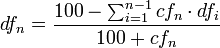
bzw. für den Zinssatz: $\sqrt[n]{\frac{100+cf_n}{100-\sum_{i=1}^{n-1} cf_n\cdot df_i}}-1$

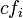wobei $\ cf_i$ der Cashflow und 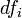$\ df_i$ Diskontfaktor des Jahres 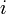$\ i$ ist.

Sonderprobleme ergeben sich daraus, dass Zero Bond Renditen nur im Jahresabstand vorhanden sind. Damit könnte die Bewertung eines alten Swaps nicht möglich sein. Dies lässt sich jedoch durch Interpolation lösen. Auf diese Weise lässt sich bspw. eine fiktive Rendite der Restlaufzeit von T=1/2 ermitteln.

Eine weitere Frage ist, ob der Bid- oder der Offerswapsatz verwendet werden soll. Hier kann der Mittelwert genommen werden.

Außerdem stellt sich die Frage der Zinsstrukturkurve im unterjährigen Bereich. Heranziehen lassen sich dafür die Geldmarktzinssätze, was aber unüblich ist, da es sich um Kassamarktzinsen handelt. Alternativ werden Geldmarkt-Futures eingesetzt, aus denen die Zinsstrukturkurve im unterjährigen Bereich mittels impliziten Terminsätzen berechnet werden kann.

Ermittlung aus Forwardpreisen

Ermittlung aus s-jährige Forwardpreisen auf eine Kuponanleihe mit x Jahren Restlaufzeit. Der mit dem s-jährigen Zinssatz abgezinste Forwardpreis entspricht dem Barwert der in s gekauften Anleihe (Zahlungen erst ab s berücksichtigt).

Statistische Verfahren

Es werden diskrete von stetigen Verfahren unterschieden. Stetige Verfahren umfassen Spline-Verfahren, das Nelson-Siegel-Verfahren und das von der Bundesbank verwendete Svensson-Verfahren (auch erweitertes Nelson-Siegel). Die Bundesbank nutzt dabei die durchschnittliche Effektivverzinsung von laufenden Kuponanleihen (insbesondere Bundesanleihen) um Zinsstrukturkurven zu ermitteln.

Als Bootstrapping bezeichnet man ein Verfahren zur Ermittlung der Spot-Rate-Strukturkurve aus Marktdaten.

Grafische Darstellung

Die Zinskurve kann folgende Ausformungen haben:

Normale (steigende) Zinskurve

Normale Zinskurve

Die Zinskurve ist meist steigend, d.h. für längere Bindungsdauern werden höhere Zinsen bezahlt. Das kann der Ausdruck dafür sein, dass der Markt höhere Zinsen in der Zukunft erwartet; ebenfalls wird die längere Bindungsdauer mit einer Liquiditätsprämie und einer Risikoprämie abgegolten.

Flache Zinskurve

Flache Zinskurve

Dies bedeutet, dass die Zinsen von der Bindungsdauer unabhängig sind. Unter der Annahme, dass der Markt eine Liquiditätsprämie und Risikoprämie zahlt, bedeutet dies, dass fallende Zinsen erwartet werden.

Inverse (fallende) Zinskurve

Inverse Zinskurve

Für langfristige Anlagen werden weniger Zinsen bezahlt als für kurzfristige Anlagen. Dies bedeutet, dass der Markt für die Zukunft stark fallende Zinsen erwartet (z.B. durch Leitzinssenkungen der Notenbank) und die Akteure folglich lieber in kurzfristige Anlagen investieren. Die dadurch entstehende Nachfrage "am langen Ende" drückt die entsprechenden Zinssätze.

Dies war in der Vergangenheit oft ein Vorzeichen für Wirtschaftskrisen. Aber es gibt auch außerordentliche wirtschaftliche Umstände, die eine inverse Zinskurve bedingen. Kurz nach der Wiedervereinigung Deutschlands war die Zinskurve beispielsweise invers.

Unregelmäßige Zinskurve

Unregelmäßige Zinskurve

Unter den unregelmäßigen Zinskurven ist die "buckelige" (wie abgebildet) die häufigste.

Anwendungen

Die Zinsstrukturkurve lässt sich einsetzen bei der Bewertung von festverzinslichen Titeln. Es lässt sich der theoretische Preis und Kurs berechnen. Auch die Sensitivität des Kurses und Preises des festverzinslichen Titels gegenüber Zinsänderungen lässt sich erfassen.

Außerdem eignet sich die Zinsstrukturkurve auch für die Berechnung von impliziten Terminzinssätzen, Szenarioanalysen und für die Bewertung von Zinsderivaten.

Arbitragemöglichkeit bei konstanter inverser Zinsstruktur

Geht eine inverse Zinsstruktur nach einem Jahr sicher wieder in dieselbe inverse Zinsstruktur über, so besteht eine Arbitragemöglichkeit.

Es bieten sich zwei Strategien an:

• Strategie A: rollierende Anlage von 1 € über zwei Jahre: EV = (1 + y(1))²
• Strategie B: Anlage von 1 € mit 2jährigem Zerobond: EV = (1 + y(2))²

Gehe Strategie A long und B short

Dann ergibt sich heute und nach einem Jahr eine Auszahlung von 0. Nach zwei Jahren besteht die Auszahlung in der Differenz: (1 + y(1))² − (1 + y(2))² > 0 aufgrund der inversen Zinsstruktur.

Sonstige Ermittlung von Arbitragemöglichkeiten

Ob eine Zinsstrukturkurve Arbitragemöglichkeiten bietet lässt sich feststellen, indem ein Arbitragetableau gebildet wird, oder eine Umrechnung in die Terminkurve/Diskontstrukturkurve erfolgt

• Bei Terminzinssätzen gibt es eine Arbitragemöglichkeit dann und nur dann wenn es negative Terminzinssätze gibt. (und man Bargeld "unter der Bettdecke" halten kann)
• Bei Diskontstrukturkurven gibt es eine Arbitragemöglichkeit dann und nur dann wenn sie nicht fallend mit der Zeit ist.

Normale Zinsstruktur und einperiodige Terminpreise

Eine normale Zinsstruktur muss nicht steigende einperiodige Terminzinssätze bedeuten.

Eine normale Zinsstrukturkurve liegt vor, wenn $r(s,t)>y(s) \$

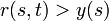
Bsp.: y(2)=0,1 und r(2,3)=0,16, dann ist y(3)= 0,12.., sei y(3)<r(3,4)=0,14; so ist y(4)=0,125. wir haben eine normale Zinsstruktur y(2)=0,1 y(3)=0,12 y(4)=0,125, aber nicht steigende Terminzinsen r(2,3)=0,16, r(1,4)=0,14.

Zinsstruktur und zukünftige Spotzinssätze

Die Zinsstruktur ist eine Momentaufnahme bezüglich unterschiedlicher Restlaufzeiten und lässt keine Aussage über die Zukunft zu. Es lassen sich lediglich die impliziten Terminzinssätze berechnen. Diese sind aber in der Regel nicht identisch mit den zukünftigen Spotzinssätzen.

Literatur

• Jessica James and Nick Webber (2000). Interest Rate Modelling. Wiley Finance. ISBN 0-471-97523-0.
• Riccardo Rebonato (2002). Modern Pricing of Interest-Rate Derivatives. Princeton University Press. ISBN 0-691-08973-6.
• Andrew J. G. Cairns (2004). Interest Rate Models An Introduction. Princeton University Press. ISBN 0-691-11894-9.
• Damiano Brigo, Fabio Mercurio: Interest Rate Models. Theory and Practice: With Smile, Inflation and Credit (Springer Finance) ISBN 978-3540221494

Weblinks

• Tägliche Zinsstruktur am Rentenmarkt bei Bundesbank
• Zinsstrukturkurven bei yahoo
• Erklärungen bei riskglossary (engl.)
• deutsche Zinskurven bei Bloomberg (engl.)
• Zeitungsartikel der FAZ
• Einführung in die Mathematik der Zinsstukturmodelle (pdf)
• dynamische US_Zinskurven seit 2003
• Artikel der Bundesbank: Schätzung von Zinsstrukturkurven (pdf)