- Zirkulante Matrix
-
Eine zirkulante Matrix ist eine spezielle Toeplitz-Matrix, bei der jeder Zeilenvektor relativ zum darüberliegenden Zeilenvektor um einen Eintrag nach rechts verschoben ist. Anders ausgedrückt ist sie ein Beispiel für ein Lateinisches Quadrat. Zirkulante Matrizen können per diskreter Fourier-Transformation einfach gelöst werden.
Definition
Eine
 Matrix C folgender Form
Matrix C folgender Formnennt man zirkulante Matrix.
Lösen von Gleichungssystemen mit zirkulanten Matrizen
Gegeben sei ein Gleichungssystem der Form
wobei
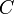 eine zirkulante, quadratische Matrix der Größe
eine zirkulante, quadratische Matrix der Größe 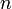 sei. Dann kann man die Gleichung als zyklische Faltung schreiben:
sei. Dann kann man die Gleichung als zyklische Faltung schreiben:Hierbei ist
 die erste Spalte / Zeile von
die erste Spalte / Zeile von 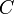 , und die Vektoren
, und die Vektoren  ,
, 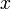 und
und 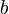 sind in beide Richtungen zyklisch erweitert. Dann kann man schreiben:
sind in beide Richtungen zyklisch erweitert. Dann kann man schreiben:so dass gilt:
Dieser Ansatz ist bedeutend schneller als das Gaußsche Eliminationsverfahren, besonders wenn eine schnelle Fourier-Transformation verwendet wird.
Wikimedia Foundation.

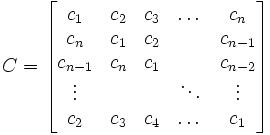
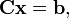
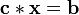
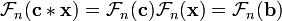
![\ \mathbf{x} = \mathcal{F}_{n}^{-1}
\left [
\left (
\frac{(\mathcal{F}_n(\mathbf{b}))_{\nu}}
{(\mathcal{F}_n(\mathbf{c}))_{\nu}}
\right )_{\nu \in \mathbf{Z}}
\right ].](/pictures/dewiki/56/88e95380fbdd8f8da59e5dc7107dcb86.png)