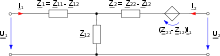Zweitor

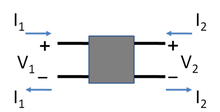
Ein Zweitor beschreibt ein elektrisches Netzwerk mit vier Anschlüssen, bei dem je zwei Anschlüsse zu einem so genannten Tor zusammengefasst werden. Ein Tor liegt dann vor, wenn der elektrische Strom durch beide Anschlüsse eines Tors gegengleich ist. Ein Zweitor ist damit eine spezielle Form eines Vierpols. Die Bezeichnung Vierpol stammt aus dem Jahr 1921 von Franz Breisig. Die bei Zweitoren übliche Matrizenschreibweise geht auf Felix Strecker aus dem Jahr 1941 zurück.^[1]

Ein Zweitor ist ein Spezialfall eines n-Tores (auch als Mehrtor bezeichnet).

Allgemeines

Allgemeines Zweitor

Ein Zweitor ist eine spezielle Form von Vierpol. Bei einem allgemeinen Vierpol muss die Torbedingung nicht gelten, womit die im nachfolgenden dargestellten Zweitorparameter und die mathematische Beschreibung mit Hilfe von Matrizen nur bei linearen Zweitoren und nicht bei allgemeinen Vierpolen anwendbar ist.

Vor allem in älterer Fachliteratur werden die Begriffe Zweitor und Vierpol synonym verwendet, wenngleich dabei unter dem Begriff Vierpol implizit Zweitore verstanden werden. Oft werden die Tore eines Zweitors auch als Eingang und als Ausgang bezeichnet.

Das Klemmenverhalten eines linearen Zweitors wird durch seine Übertragungsfunktion oder seinen Frequenzgang beschrieben. Hieraus lassen sich Zweitorgleichungen gewinnen, aus denen Zweitorparameter zur Modellbildung gewonnen werden können.

Klassifizierung

Zweitore lassen sich anhand ihres Klemmenverhaltens, d. h. als Blackbox ohne genaue Kenntnis ihrer inneren Struktur, wie folgt, klassifizieren:

• Hängen die Zweitorströme und -spannungen linear voneinander ab, so nennt man das Zweitor linear, sonst nichtlinear. Nur für lineare Zweitore gilt die im Folgenden beschriebene Matrizendarstellung der Zweitorparameter.
• Enthält ein Zweitor keine Energiequellen (ungesteuert oder gesteuert), so nennt man es passiv, sonst aktiv. Geht in einem (passiven) Zweitor keine Energie verloren, weil es nur Blindschaltelemente enthält, so nennt man es Reaktanzzweitor.
• Ändert sich das Verhalten eines Zweitors beim Vertauschen von Eingangs- und Ausgangsklemmenpaar nicht, so nennt man es symmetrisch, sonst unsymmetrisch.
• Ändert sich das Verhältnis von Eingangsstrom und Ausgangsspannung bei kurzgeschlossenem Eingang beim Vertauschen von Eingangs- und Ausgangsklemmenpaar nicht, so nennt man ein solches Zweitor reziprok oder umkehrbar (Reziprozitätstheorem, Umkehrungssatz).
• Hat eine sich (durch Belastung) verändernde Ausgangsgröße keinen Einfluss auf eine Eingangsgröße, so ist das Zweitor rückwirkungsfrei.

Zweitorgleichungen und Parameter

Schaltung zur Impedanzmatrix

Bezeichnen U₁ die Spannung und I₁ den Strom am Eingangsklemmenpaar und U₂ und I₂ die entsprechenden Größen am Ausgangsklemmenpaar, dann können jeweils zwei gesuchte Größen aus den beiden anderen gegebenen Größen durch ein Paar von Zweitorgleichungen berechnet werden. Diese sind im Allgemeinen nichtlineare Differentialgleichungen.

Für lineare Zweitore gehen sie, eventuell unter Anwendung der symbolischen Methode der Wechselstromrechnung oder der Laplacetransformation, in ein Paar lineare Gleichungen mit vier das Zweitor beschreibenden Zweitorparametern über.

Unter der Voraussetzung der Existenz lassen sich diese Zweitorgleichungen in Form von Matrixgleichungen angeben. Eingeprägte Ströme und Spannungen werden je nach Bedarf zu diesen Gleichungen als Matrizen hinzu addiert. Die angegebenen Berechnungsvorschriften dienen zur Bestimmung der Matrizen für ein beliebiges, bekanntes Zweitor, wie zum Beispiel ein Feedback-Netzwerk einer Verstärkerschaltung.

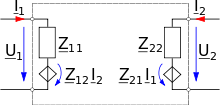
Z-Charakteristik	$\begin{pmatrix}U_1 \\ U_2\end{pmatrix} = \begin{pmatrix}Z_{11} = \left.\frac{U_1}{I_1}\right|_{I_2=0} & Z_{12} = \left.\frac{U_1}{I_2}\right|_{I_1=0} \\ Z_{21} = \left.\frac{U_2}{I_1}\right|_{I_2=0} & Z_{22} = \left.\frac{U_2}{I_2}\right|_{I_1=0}\end{pmatrix} \cdot \begin{pmatrix}I_1 \\ I_2\end{pmatrix}$	$\mathbf{Z}$: Impedanzmatrix, existent, falls die Torströme (I1 bzw. I2) unabhängig wählbar sind.
Y-Charakteristik	$\begin{pmatrix}I_1 \\ I_2\end{pmatrix} = \begin{pmatrix}Y_{11} = \left.\frac{I_1}{U_1}\right|_{U_2=0} & Y_{12} = \left.\frac{I_1}{U_2}\right|_{U_1=0} \\ Y_{21} = \left.\frac{I_2}{U_1}\right|_{U_2=0} & Y_{22} = \left.\frac{I_2}{U_2}\right|_{U_1=0} \end{pmatrix} \cdot \begin{pmatrix}U_1 \\ U_2\end{pmatrix}$	$\mathbf{Y}$: Admittanzmatrix, existent, falls die Torspannungen (U1 bzw. U2) unabhängig wählbar sind.
H-Charakteristik	$\begin{pmatrix}U_1 \\ I_2\end{pmatrix} = \begin{pmatrix}H_{11} = \left.\frac{U_1}{I_1}\right|_{U_2=0} & H_{12} = \left.\frac{U_1}{U_2}\right|_{I_1=0} \\ H_{21} = \left.\frac{I_2}{I_1}\right|_{U_2=0} & H_{22} = \left.\frac{I_2}{U_2}\right|_{I_1=0} \end{pmatrix} \cdot \begin{pmatrix}I_1 \\ U_2\end{pmatrix}$	$\mathbf{H}$: Hybridmatrix, existent falls I1 bzw. U2 unabhängig wählbar sind.
P-Charakteristik	$\begin{pmatrix}I_1 \\ U_2\end{pmatrix} = \begin{pmatrix}P_{11} = \left.\frac{I_1}{U_1}\right|_{I_2=0} & P_{12} = \left.\frac{I_1}{I_2}\right|_{U_1=0} \\ P_{21} = \left.\frac{U_2}{U_1}\right|_{I_2=0} & P_{22} = \left.\frac{U_2}{I_2}\right|_{U_1=0} \end{pmatrix} \cdot \begin{pmatrix}U_1 \\ I_2\end{pmatrix}$	$\mathbf{P}$: inverse Hybridmatrix, existent falls U1 bzw. I2 unabhängig wählbar sind.
A-Charakteristik	$\begin{pmatrix}U_1 \\ I_1\end{pmatrix} = \begin{pmatrix}A_{11} = \left.\frac{U_1}{U_2}\right|_{I_2=0} & A_{12} = \left.\frac{-U_1}{I_2}\right|_{U_2=0} \\ A_{21} = \left.\frac{I_1}{U_2}\right|_{I_2=0} & A_{22} = \left.\frac{-I_1}{I_2}\right|_{U_2=0} \end{pmatrix} \cdot \begin{pmatrix}U_2 \\ -I_2\end{pmatrix}$	$\mathbf{A}$: Kettenmatrix
B-Charakteristik	$\begin{pmatrix}U_2 \\ I_2\end{pmatrix} = \begin{pmatrix}B_{11} = \left.\frac{U_2}{U_1}\right|_{I_1=0} & B_{12} = \left.\frac{-U_2}{I_1}\right|_{U_1=0} \\ B_{21} = \left.\frac{I_2}{U_1}\right|_{I_1=0} & B_{22} = \left.\frac{-I_2}{I_1}\right|_{U_1=0} \end{pmatrix} \cdot \begin{pmatrix}U_1 \\ -I_1\end{pmatrix}$	$\mathbf{B}$: inverse Kettenmatrix

hierbei gilt im Fall der Existenz:

$\mathbf{Y}= \mathbf{Z}^{-1}$

$\mathbf{P}= \mathbf{H}^{-1}$

$\mathbf{B}= \mathbf{A}^{-1}$

Der Vorteil dieser Schreibweisen ist, dass die Parameter (Z_xy, etc.) bekannte Bauteilwerte repräsentieren und daher als Zahlenwerte gegeben sind. Nun kann der Zusammenhang zwischen den Eingangs- und Ausgangsströmen, sowie den Eingangs- und Ausgangsspannungen leicht abgelesen werden.

Hinweis: Statt dem Symbol $\mathbf{P}$ werden auch $\mathbf{H'}$ oder $\mathbf{C}$ und statt dem Symbol $\mathbf{B}$ wird auch $\mathbf{A'}$ verwendet.

Umrechnung der Matrizen

	$\mathbf{Z}$	$\mathbf{Y}$	$\mathbf{H}$	$\mathbf{P}$	$\mathbf{A}$
$\mathbf{Z}$	$\begin{array}{cc} Z_{11} & Z_{12} \\ Z_{21} & Z_{22} \end{array}$	$\begin{array}{cc} \frac{Y_{22}}{\det \mathbf{Y}} & \frac{-Y_{12}}{\det \mathbf{Y}} \\ \frac{-Y_{21}}{\det \mathbf{Y}} & \frac{Y_{11}}{\det \mathbf{Y}} \end{array}$	$\begin{array}{cc} \frac{\det \mathbf{H}}{H_{22}} & \frac{H_{12}}{H_{22}} \\ \frac{-H_{21}}{H_{22}} & \frac{1}{H_{22}} \end{array}$	$\begin{array}{cc} \frac{1}{P_{11}} & \frac{-P_{12}}{P_{11}} \\ \frac{P_{21}}{P_{11}} & \frac{\det \mathbf{P}}{P_{11}} \end{array}$	$\begin{array}{cc} \frac{A_{11}}{A_{21}} & \frac{\det \mathbf{A}}{A_{21}} \\ \frac{1}{A_{21}} & \frac{A_{22}}{A_{21}} \end{array}$
$\mathbf{Y}$	$\begin{array}{cc} \frac{Z_{22}}{\det \mathbf{Z}} & \frac{-Z_{12}}{\det \mathbf{Z}} \\ \frac{-Z_{21}}{\det \mathbf{Z}} & \frac{Z_{11}}{\det \mathbf{Z}} \end{array}$	$\begin{array}{cc} Y_{11} & Y_{12} \\ Y_{21} & Y_{22} \end{array}$	$\begin{array}{cc} \frac{1}{H_{11}} & \frac{-H_{12}}{H_{11}} \\ \frac{H_{21}}{H_{11}} & \frac{\det \mathbf{H}}{H_{11}} \end{array}$	$\begin{array}{cc} \frac{\det \mathbf{P}}{P_{22}} & \frac{P_{12}}{P_{22}} \\ \frac{-P_{21}}{P_{22}} & \frac{1}{P_{22}} \end{array}$	$\begin{array}{cc} \frac{A_{22}}{A_{12}} & \frac{-\det \mathbf{A}}{A_{12}} \\ \frac{-1}{A_{12}} & \frac{A_{11}}{A_{12}} \end{array}$
$\mathbf{H}$	$\begin{array}{cc} \frac{\det \mathbf{Z}}{Z_{22}} & \frac{Z_{12}}{Z_{22}} \\ \frac{-Z_{21}}{Z_{22}} & \frac{1}{Z_{22}} \end{array}$	$\begin{array}{cc} \frac{1}{Y_{11}} & \frac{-Y_{12}}{Y_{11}} \\ \frac{Y_{21}}{Y_{11}} & \frac{\det \mathbf{Y}}{Y_{11}} \end{array}$	$\begin{array}{cc} H_{11} & H_{12} \\ H_{21} & H_{22} \end{array}$	$\begin{array}{cc} \frac{P_{22}}{\det \mathbf{P}} & \frac{-P_{12}}{\det \mathbf{P}} \\ \frac{-P_{21}}{\det \mathbf{P}} & \frac{P_{11}}{\det \mathbf{P}} \end{array}$	$\begin{array}{cc} \frac{A_{12}}{A_{22}} & \frac{\det \mathbf{A}}{A_{22}} \\ \frac{-1}{A_{22}} & \frac{A_{21}}{A_{22}} \end{array}$
$\mathbf{P}$	$\begin{array}{cc} \frac{1}{Z_{11}} & \frac{-Z_{12}}{Z_{11}} \\ \frac{Z_{21}}{Z_{11}} & \frac{\det \mathbf{Z}}{Z_{11}} \end{array}$	$\begin{array}{cc} \frac{\det \mathbf{Y}}{Y_{22}} & \frac{Y_{12}}{Y_{22}} \\ \frac{-Y_{21}}{Y_{22}} & \frac{1}{Y_{22}} \end{array}$	$\begin{array}{cc} \frac{H_{22}}{\det \mathbf{H}} & \frac{-H_{12}}{\det \mathbf{H}} \\ \frac{-H_{21}}{\det \mathbf{H}} & \frac{H_{11}}{\det \mathbf{H}} \end{array}$	$\begin{array}{cc} P_{11} & P_{12} \\ P_{21} & P_{22} \end{array}$	$\begin{array}{cc} \frac{A_{21}}{A_{11}} & \frac{-\det \mathbf{A}}{A_{11}} \\ \frac{1}{A_{11}} & \frac{A_{12}}{A_{11}} \end{array}$
$\mathbf{A}$	$\begin{array}{cc} \frac{Z_{11}}{Z_{21}} & \frac{\det \mathbf{Z}}{Z_{21}} \\ \frac{1}{Z_{21}} & \frac{Z_{22}}{Z_{21}} \end{array}$	$\begin{array}{cc} \frac{-Y_{22}}{Y_{21}} & \frac{-1}{Y_{21}} \\ \frac{-\det \mathbf{Y}}{Y_{21}} & \frac{-Y_{11}}{Y_{21}} \end{array}$	$\begin{array}{cc} \frac{-\det \mathbf{H}}{H_{21}} & \frac{-H_{11}}{H_{21}} \\ \frac{-H_{22}}{H_{21}} & \frac{-1}{H_{21}} \end{array}$	$\begin{array}{cc} \frac{1}{P_{21}} & \frac{P_{22}}{P_{21}} \\ \frac{P_{11}}{P_{21}} & \frac{\det \mathbf{P}}{P_{21}} \end{array}$	$\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array}$

Ersatzschaltungen

Zur Vereinfachung von Rechnungen können komplexe Zweitore mithilfe entsprechender Zweitorparameter zu vereinfachten Schaltungen zusammengefasst werden. Die Ersatzschaltungen stellen keine Anleitung zur physikalischen Realisierung dar.

T-Ersatzschaltung

Die T-Ersatzschaltung ermöglicht die Darstellung eines beliebigen Zweitors mithilfe der Ersatzimpedanzen. Bei umkehrbaren Zweitoren entfällt die gesteuerte Spannungsquelle.

π-Ersatzschaltung

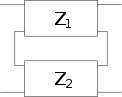
Die π-Ersatzschaltung ermöglicht die Darstellung eines beliebigen Zweitors mithilfe der Ersatzadmittanzen. Bei umkehrbaren Zweitoren entfällt die gesteuerte Stromquelle.

Zusammenschalten

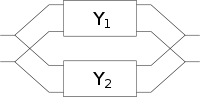
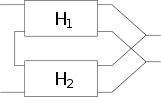
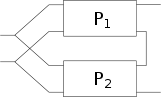
Zwei Zweitore können unter der Voraussetzung, dass die oben genannte Torbedingung an mindestens einem Tor erfüllt wird, zu einem neuen Zweitor zusammengeschaltet werden. Die Parameter des neu entstandenen Zweitors lassen sich aus den Parametern der beiden verschalteten Zweitore errechnen. Für jede Verschaltungsart gibt es eine Charakteristik, mit der sich die Verschaltung besonders gut berechnen lässt. Es gibt insgesamt fünf verschiedene Möglichkeiten Zweitore zusammenzuschalten:

Beschreibungsart	Darstellung	Mathematische Beschreibung		Beschreibungsart	Darstellung	Mathematische Beschreibung
Reihenschaltung		$\mathbf{Z_{ges}}=\mathbf{Z_1}+\mathbf{Z_2}$		Parallelschaltung		$\mathbf{Y_{ges}}=\mathbf{Y_1}+\mathbf{Y_2}$
Hybridschaltung oder Reihen-Parallelschaltung		$\mathbf{H_{ges}}=\mathbf{H_1}+\mathbf{H_2}$		inverse Hybridschaltung oder Parallel-Reihenschaltung		$\mathbf{P_{ges}}=\mathbf{P_1}+\mathbf{P_2}$ bzw. $\mathbf{H'_{ges}}=\mathbf{H'_1}+\mathbf{H'_2}$ bzw. $\mathbf{C_{ges}}=\mathbf{C_1}+\mathbf{C_2}$
Kettenschaltung		$\mathbf{A_{ges}}=\mathbf{A_1}\cdot \mathbf{A_2}$ oder $\mathbf{B_{ges}}=\mathbf{B_2}\cdot \mathbf{B_1}$ bzw. $\mathbf{A'_{ges}}=\mathbf{A'_2}\cdot \mathbf{A'_1}$

Weitere Zweitorparameter

Neben der Charakterisierung eines Zweitors durch die oben beschriebenen Zweitorparameter gibt es für besondere Anwendungszwecke auch andere Darstellungsformen. So kann ein lineares Zweitor auch durch sogenannte Streuparameter beschrieben werden. Diese Darstellungsform ist vor allem im Bereich der Hochfrequenztechnik üblich, da dabei die Anschlüsse des Zweitors nicht kurzgeschlossen bzw. leerlaufen müssen, sondern im Regelfall durch ihren Leitungswellenwiderstand abgeschlossen sind.

Zwischen den S-Parametern und den oben erwähnten Y-Parametern der Admittanzmatrix eines Zweitors besteht mit dem Leitungswellenwiderstand Z_W folgender Zusammenhang:

$Y_{11} = \frac{1}{Z_w} \frac{1-S_{11}+S_{22}-\Delta_S}{1+S_{11}+S_{22}+\Delta_S}$

$Y_{12} = \frac{1}{Z_w} \frac{-2S_{12}}{1+S_{11}+S_{22}+\Delta_S}$

$Y_{21} = \frac{1}{Z_w} \frac{-2S_{21}}{1+S_{11}+S_{22}+\Delta_S}$

$Y_{22} = \frac{1}{Z_w} \frac{1+S_{11}-S_{22}-\Delta_S}{1+S_{11}+S_{22}+\Delta_S}$

mit der Abkürzung:

Δ_S = S₁₁S₂₂ − S₁₂S₂₁

Symmetrische lineare Zweitore werden für ihre Anwendung in der Theorie der Siebschaltungen (Wellenparametertheorie) durch die sogenannten Wellenparameter beschrieben. Die zwei das Zweitor beschreibenden Parameter sind dabei der Wellenwiderstand und das Wellenübertragungsmaß.

Eigenschaften

Reziproke Zweitore

Eine an Tor 1 angelegte Spannung U₁ erzeugt an Tor 2 einen Strom I₂. Wird dieselbe Spannung an Tor 2 angelegt, U₁=U₂ wird derselbe Strom I₂ an Tor 1 erzeugt. D.h. I₂=I₁ wenn U₁=U₂ ist. Reziproke Zweitore sind durch drei Zweitorparameter vollständig charakterisiert. Es gilt:

• Z₂₁ = Z₁₂
• Y₂₁ = Y₁₂
• H₂₁ = − H₁₂
• P₂₁ = − P₁₂
• $\det \mathbf{A} = 1$

Rückwirkungsfreie Zweitore

Bei einem rückwirkungsfreien Zweitor gilt:

• Z₁₂ = 0
• Y₁₂ = 0
• H₁₂ = 0
• P₁₂ = 0

Damit sind die Eingangsgrößen U₁, I₁ von den Ausgangsgrößen U₂, I₂ unabhängig.

Symmetrische Zweitore

Für symmetrische Zweitore gilt:

• Z₂₂ = Z₁₁, Z₂₁ = Z₁₂
• Y₂₂ = Y₁₁, Y₂₁ = Y₁₂
• $\det \mathbf{H} = 1$, H₂₁ = − H₁₂
• $\det \mathbf{P} = 1$, P₂₁ = − P₁₂
• A₂₂ = A₁₁, $\det \mathbf{A} = 1$

Symmetrische Zweitore sind somit durch zwei Zweitorparameter vollständig charakterisiert. Symmetrische Zweitore sind immer reziprok, jedoch sind reziproke Zweitore nicht immer symmetrisch.

Quellen

• Vorlesung – Netzwerke 3. Institut für Grundlagen und Theorie der Elektrotechnik, Technische Universität Graz (Diese Thematik wird als Mehrtortheorie bezeichnet. Unter diesem Titel sollten daher weitere Quellen auffindbar sein).
• Vorlesung – Dynamische Netzwerke. Institut für Grundlagen der Elektrotechnik und Elektronik, Technische Universität Dresden

Literatur

• Richard Feldtkeller: Einführung in die Vierpoltheorie der elektrischen Nachrichtentechnik. Hirzel, Stuttgart 1976, ISBN 3-7776-0319-8.
• Lorenz-Peter Schmidt, Gerd Schaller, Siegfried Martius: Grundlagen der Elektrotechnik 3. Netzwerke. Pearson Studium, München 2006, ISBN 3-8273-7107-4.
• Eugen Philippow: Grundlagen der Elektrotechnik. Akademische Verlagsgesellschaft Geest & Portig K.-G., Leipzig 1966.
• Heinrich Schröder: Elektrische Nachrichtentechnik Band I. Verlag für Radio-Foto-Kinotechnik GmbH, Berlin-Borsigwalde 1966.

Weblinks

• Ronny Harbich: Passive Zweitore. 2005, abgerufen am 18. Januar 2010.

Einzelnachweise

1. ↑ Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Theoretische Elektrotechnik. 18. Auflage. Springer, ISBN 978-3-540-78589-7, S. 63 bis 75.