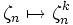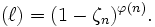Zyklotomischer Körper

Kreisteilungskörper sind Studienobjekte des mathematischen Teilgebietes der algebraischen Zahlentheorie. Sie sind in gewisser Hinsicht besonders einfache Verallgemeinerungen des Körpers der rationalen Zahlen.

Definition: Es sei n > 2 eine natürliche Zahl. Dann ist der n-te Kreisteilungskörper diejenige Körpererweiterung 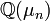$\mathbb Q(\mu_n)$ von $\mathbb Q$, die durch Adjunktion der Menge μ_n aller n-ten Einheitswurzeln entsteht.

Eigenschaften

• Ist ζ_n eine primitive n-te Einheitswurzel, so ist das Minimalpolynom von ζ_n das n-te Kreisteilungspolynom Φ_n, deshalb ist

$\mathbb Q(\mu_n)\cong\mathbb Q(\zeta_n)\cong\mathbb Q[T]/(\Phi_n(T)).$

Insbesondere ist der Körpergrad $[\mathbb Q(\mu_n):\mathbb Q]=\varphi(n)$ mit der eulerschen φ-Funktion.

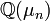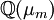• Zwei Kreisteilungskörper $\mathbb Q(\mu_n)$ und $\mathbb Q\mathbb(\mu_m)$ mit n < m sind genau dann gleich, wenn n ungerade ist und m = 2n gilt.

• Die Adjunktion der m-ten Einheitswurzeln zu 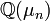$\mathbb Q(\mu_n)$ ergibt 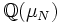$\mathbb Q(\mu_N)$ mit N = kgV(m,n).

• Die Erweiterung 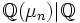$\mathbb Q(\mu_n)|\mathbb Q$ ist galoissch. Die Galoisgruppe ist isomorph zu 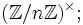$(\mathbb Z/n\mathbb Z)^\times;$ ist ζ_n eine primitive n-te Einheitswurzel, so entspricht einem Element 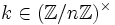$k\in(\mathbb Z/n\mathbb Z)^\times$ der durch

$\zeta_n\mapsto\zeta_n^k$

definierte Automorphismus von $\mathbb Q(\mu_n).$

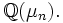
• Der Ganzheitsring von 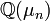$\mathbb Q(\mu_n)$ ist $\mathbb Z[\zeta_n]$ mit einer beliebigen primitiven n-ten Einheitswurzel ζ_n. Insbesondere ist der Ganzheitsring von 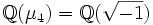$\mathbb Q(\mu_4)=\mathbb Q(\sqrt{-1})$ isomorph zum Ring der ganzen gaußschen Zahlen, der Ganzheitsring von 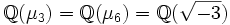$\mathbb Q(\mu_3)=\mathbb Q(\mu_6)=\mathbb Q(\sqrt{-3})$ ist isomorph zum Ring der Eisenstein-Zahlen.

• Eine Primzahl 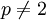$p\ne2$ ist genau dann verzweigt in 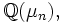$\mathbb Q(\mu_n),$ wenn p ein Teiler von n ist. p ist genau dann voll zerlegt, wenn 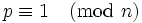$p\equiv 1\pmod n$ gilt.

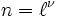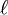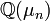• Ist $n=\ell^\nu$ eine Primzahlpotenz und ζ_n eine primitive n-te Einheitswurzel, so ist $\ell$ in $\mathbb Q(\mu_n)$ rein verzweigt, und das Primideal über 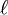$\ell$ ist ein Hauptideal, das von 1 − ζ_n erzeugt wird:

$(\ell)=(1-\zeta_n)^{\varphi(n)}.$

Satz von Kronecker-Weber

Der Satz von Kronecker-Weber (nach L. Kronecker und H. Weber) besagt, dass jeder algebraische Zahlkörper mit abelscher Galoisgruppe in einem Kreisteilungskörper enthalten ist. Die maximale abelsche Erweiterung von $\mathbb Q$ entsteht also durch Adjunktion aller Einheitswurzeln.