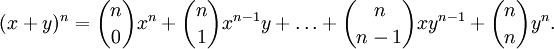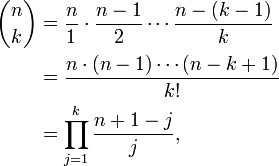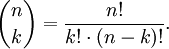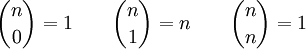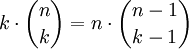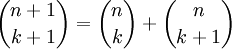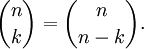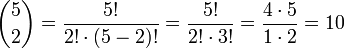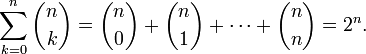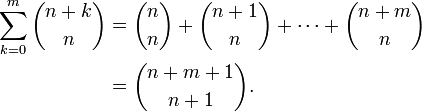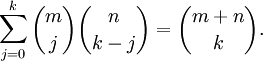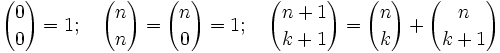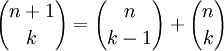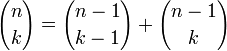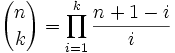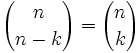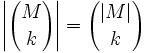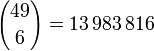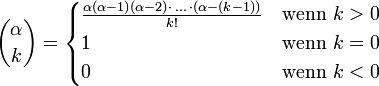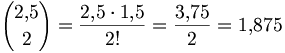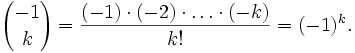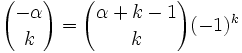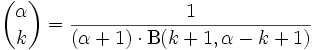Über

Der Binomialkoeffizient ist eine mathematische Funktion, mit der sich eine der Grundaufgaben der Kombinatorik lösen lässt. Er gibt an, auf wieviele verschiedene Arten man k Objekte aus einer Menge von n verschiedenen Objekten auswählen kann (ohne Zurücklegen, ohne Beachtung der Reihenfolge). Der Binomialkoeffizient „49 über 6“ entspricht damit beispielsweise der Anzahl der möglichen Ziehungen beim Lotto.

Ein Binomialkoeffizient hängt von zwei Zahlen n und k ab. Er wird mit dem Symbol

$\binom nk$

geschrieben und als „n über k“, „k aus n“ oder „n tief k“ gesprochen.

Den Namen erhielten diese Zahlen, da sie als Koeffizienten in den Potenzen des Binoms (x + y) auftreten; es gilt der sogenannte binomische Lehrsatz

$(x+y)^n = \binom n0 x^n + \binom n1 x^{n-1} y + \ldots + \binom n{n-1} x y^{n-1} + \binom nn y^n.$

Eine Erweiterung des aus der Kombinatorik stammenden Binomialkoeffizienten stellt der allgemeine Binomialkoeffizient dar, der in der Analysis verwendet wird.

Definition

Für eine komplexe Zahl n und eine nichtnegative ganze Zahl k ist der Binomialkoeffizient „n über k“ auf folgende Weise definiert:

$\begin{align} \binom nk &= \frac n1 \cdot \frac{n-1}2 \cdots \frac{n-(k-1)}k\\ &= \frac{n\cdot(n-1) \cdots (n-k+1)}{k!}\\ &= \prod_{j=1}^k \frac{n + 1 - j}j, \end{align}$

wobei k! die Fakultät von k bezeichnet. Das leere Produkt (k = 0) ist dabei 1.

Handelt es sich bei n um eine nichtnegative ganze Zahl mit 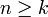$n\geq k$, so kann man die aus der Kombinatorik bekannte Definition verwenden:

$\binom nk = \frac{n!}{k! \cdot (n-k)!}.$

Eigenschaften

Für nichtnegative ganze Zahlen n und k ist $\binom nk$ stets eine nichtnegative ganze Zahl. Ist dabei k > n, so ist $\binom nk=0$.

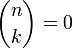Rechenregeln

$\binom n0 = 1 \qquad \binom n1 = n \qquad \binom nn = 1$

$k \cdot \binom nk = n \cdot \binom{n-1}{k-1}$

$\binom{n+1}{k+1} = \binom nk + \binom n{k+1}$

(sämtliche Regeln gelten auch für die Verallgemeinerung mit reellen oder komplexen Werten für n)

Symmetrie der Binomialkoeffizienten

Ganzzahlige Binomialkoeffizienten sind symmetrisch im Sinne von

$\binom nk = \binom n{n-k}.$

Beispiel

$\binom 5 3 = \binom 5 {5-3} = \binom 5 2$

$\binom 5 3 = \frac{5!}{3! \cdot (5-3)!} = \frac{5!}{3! \cdot 2!} = \frac{1\cdot 2\cdot 3\cdot 4\cdot 5}{(1\cdot 2\cdot 3) \cdot (1\cdot 2)} = \frac{4\cdot 5}{1\cdot 2} = 10$

$\binom 5 2 = \frac{5!}{2! \cdot (5-2)!} = \frac{5!}{2! \cdot 3!} = \frac{4\cdot 5}{1\cdot 2} = 10$

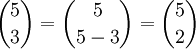
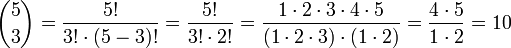
Summen von Binomialkoeffizienten

$\sum_{k=0}^n \binom nk = \binom n0 + \binom n1 + \dotsb + \binom nn = 2^n.$

Dieser Formel liegt ein kombinatorischer Sachverhalt zu Grunde. Die Summe aller Binomialkoeffizienten „n über …“ entspricht der Mächtigkeit der Potenzmenge einer n-elementigen Menge. Die Formel lässt sich auch aus dem binomischen Lehrsatz herleiten, indem man x = y = 1 setzt.

Summe alternierender Binomialkoeffizienten

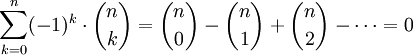$\sum_{k=0}^n (-1)^k \cdot \binom nk = \binom n0 - \binom n1 + \binom n2 - \dotsb = 0$ für n > 0.

Diese Formel folgt aus der Symmetrie des Binomialkoeffizienten. Sie lässt sich zudem aus dem binomischen Lehrsatz herleiten, indem man x = 1 und y = − 1 (oder x = − 1 und y = 1) setzt.

Summe verschobener Binomialkoeffizienten

$\begin{align} \sum_{k=0}^m \binom{n+k}n &= \binom nn + \binom{n+1}n + \dotsb + \binom{n+m}n\\ &= \binom{n+m+1}{n+1}. \end{align}$

Vandermondesche Identität

$\sum_{j=0}^k \binom mj \binom n{k-j} = \binom{m+n}k.$

Es gibt auch hier ein kombinatorisches Argument: Die rechte Seite entspricht der Anzahl von k-elementigen Teilmengen einer (m+n)-elementigen Menge von Kugeln. Man kann sich nun vorstellen, dass die Kugeln zwei verschiedene Farben haben: m Kugeln seien rot und n Kugeln grün. Eine k-elementige Teilmenge besteht dann aus einer gewissen Anzahl j von roten Kugeln und k-j vielen grünen. Für jedes mögliche j gibt der entsprechende Summand auf der linken Seite die Anzahl der Möglichkeiten für solch eine Aufteilung in rote und grüne Kugeln an. Die Summe liefert die Gesamtzahl.

Rekursive Darstellung und Pascalsches Dreieck

Für den Binomialkoeffizienten nichtnegativer ganzer Zahlen n und k hat man folgende rekursive Darstellung:

${0 \choose 0} = 1;\quad {n \choose n} = {n \choose 0} = 1;\quad {n+1 \choose k+1} = {n \choose k} + {n \choose k+1}$

Diese Formel eignet sich auch, um alle Binomialkoeffizienten bis zu einer vorgegebenen Schranke für n zu bestimmen, ein Schema dazu ist das Pascalsche Dreieck: Dort entspricht sie der Konstruktionsvorschrift, dass jede Zahl die Summe der beiden über ihr stehenden Zahlen ist (in der Formel oben k durch k - 1 ersetzen):

${n+1 \choose k} = {n \choose k-1} + {n \choose k}$

oder andersherum (n durch n − 1 ersetzen):

${n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}$

Den Koeffizienten 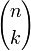$n \choose k$ findet man dabei in der (n + 1)-ten Zeile, an der (k + 1)-ten Stelle (da es keine »nullte Zeile/Stelle« gibt):

Anders dargestellt:

${0 \choose 0}$
${1 \choose 0}\quad{1 \choose 1}$
${2 \choose 0}\quad{2 \choose 1}\quad{2 \choose 2}$
${3 \choose 0}\quad{3 \choose 1}\quad{3 \choose 2}\quad{3 \choose 3}$
${4 \choose 0}\quad{4 \choose 1}\quad{4 \choose 2}\quad{4 \choose 3}\quad{4 \choose 4}$
${5 \choose 0}\quad{5 \choose 1}\quad{5 \choose 2}\quad{5 \choose 3}\quad{5 \choose 4}\quad{5 \choose 5}$
${6 \choose 0}\quad{6 \choose 1}\quad{6 \choose 2}\quad{6 \choose 3}\quad{6 \choose 4}\quad{6 \choose 5}\quad{6 \choose 6}$
${7 \choose 0}\quad{7 \choose 1}\quad{7 \choose 2}\quad{7 \choose 3}\quad{7 \choose 4}\quad{7 \choose 5}\quad{7 \choose 6}\quad{7 \choose 7}$

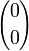
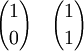
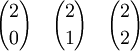
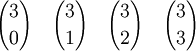
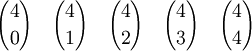
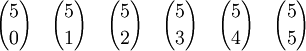
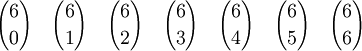
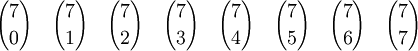
Algorithmus zur effizienten Berechnung

Für ganzzahlige n existiert ein effizienter Algorithmus, der die Produktformel

${n \choose k} = \prod_{i=1}^k \frac {n + 1 - i} i$

des Binomialkoeffizienten anwendet. Auf Grund des stetigen Wechsels zwischen Multiplikation und Division wachsen die Zwischenergebnisse nicht unnötig an. Zusätzlich sind auch alle Zwischenergebnisse natürliche Zahlen.

Um unnötigen Rechenaufwand zu vermeiden, berechnet man im Fall k > n / 2 den Binomialkoeffizienten:

${n\choose n-k} = {n\choose k}$

Der folgende Pseudocode verdeutlicht die Berechnung:

binomialkoeffizient(n, k)
1  wenn k = 0 dann rückgabe 1
2  wenn 2k > n
3      dann führe aus ergebnis $\leftarrow$ binomialkoeffizient(n, n-k)
4  sonst führe aus ergebnis $\leftarrow$ n
5          von i $\leftarrow$ 2 bis k
6              führe aus ergebnis $\leftarrow$ ergebnis $\cdot$ (n + 1 - i)
7                        ergebnis $\leftarrow$ ergebnis : i
8  rückgabe ergebnis

Der Binomialkoeffizient in der Kombinatorik

Binomialkoeffizienten spielen in der abzählenden Kombinatorik eine zentrale Rolle, denn 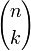$n\choose k$ ist die Anzahl der Möglichkeiten, aus einer Menge mit n Elementen k Elemente auszuwählen, wobei die Reihenfolge der ausgewählten Elemente nicht berücksichtigt wird.

Anschaulich lässt sich das so erklären: Man berechne mit n! alle möglichen Vertauschungen, suche sich k „Felder“ aus (beispielsweise 6 beim Lotto) und frage sich, wie viele Möglichkeiten es gibt, diese Felder zu besetzen. Da es keine Rolle spielt, welches „Ereignis“ sich auf welchem Feld ereignet hat, dividiert man alle unter diesen k Elementen möglichen Vertauschungen mit k! heraus. Da es auch keine Rolle spielt, wie die Anordnung auf den uninteressanten Feldern aussieht, dividiert man mit (n − k)! auch diese Vertauschungen heraus.

Formaler lässt sich dieser Sachverhalt auch so formulieren: Eine n-elementige Menge hat genau 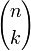$n\choose k$ k-elementige Teilmengen. Aufgrund dieser Parallele wird die Menge aller k-elementigen Teilmengen einer Menge M gelegentlich auch mit 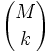$M\choose k$ bezeichnet. Mit dieser Schreibweise gilt dann für jede endliche Menge M:

$\left|{M\choose k}\right| = {\left|M\right| \choose k}$

Beispiel

Die Anzahl der möglichen Ziehungen beim deutschen Lotto 6 aus 49 (ohne Zusatzzahl oder Superzahl) lässt sich so berechnen:

${49 \choose 6} = 13\,983\,816$

Der Kehrwert 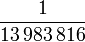$\frac{1}{13\,983\,816}$ gibt dann die Wahrscheinlichkeit an, mit einem Tipp 6 Richtige zu erzielen. Die Wahrscheinlichkeit für 5 Richtige bei 6 aus 49 lässt sich jedoch nicht mehr durch einen einzelnen Binomialkoeffizienten berechnen. Stattdessen benötigt man die Hypergeometrische Verteilung, in deren Berechnung dann mehrere Binomialkoeffizienten ausgewertet werden müssen.

Kombinatorische Beweise

Die kombinatorische Deutung erlaubt auch einfache Beweise von Relationen zwischen Binomialkoeffizienten. Beispiel: Für 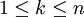$1\leq k\leq n$ gilt:

${n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}$

Beweis: Es sei X eine n-elementige Menge und $x\in X$ ein festes Element. Dann zerfallen die k-elementigen Teilmengen von X in zwei Klassen:

• die Teilmengen, die x enthalten; sie bestehen also aus x zusammen mit einer (k − 1)-elementigen Teilmenge der (n − 1)-elementigen Menge $X\setminus\{x\}$
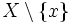
• die Teilmengen, die x nicht enthalten; sie sind k-elementige Teilmengen der (n − 1)-elementigen Menge $X\setminus\{x\}$.

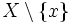Verallgemeinerung

Eine Verallgemeinerung, die in der Analysis eine Rolle spielt, erhält man, wenn man für n eine beliebige reelle oder komplexe Zahl α zulässt, aber k weiterhin als ganzzahlig voraussetzt. In diesem Fall ist

${\alpha \choose k} = \begin{cases}\frac{\alpha (\alpha - 1)(\alpha - 2) \cdot \, \dots \, \cdot (\alpha - (k - 1))}{k!} &\mbox{wenn } k>0\\ 1 &\mbox{wenn } k=0\\ 0 &\mbox{wenn } k<0 \end{cases}$

der Binomialkoeffizient „α über k“ (das leere Produkt im Fall k = 0 ist definiert als 1). Diese Definition stimmt für nichtnegative ganzzahlige α mit der ersten überein.

Beispielsweise ist

${2{,}5 \choose 2} = \frac{2{,}5\cdot 1{,}5}{2!} = \frac{3{,}75}{2} = 1{,}875$

und

${-1 \choose k} = \frac{(-1)\cdot (-2) \cdot \dots \cdot (-k)}{k!} = (-1)^k.$

Allgemein lässt sich folgende Relation angeben, um das Vorzeichen aus dem ersten Parameter zu extrahieren:

${-\alpha \choose k} = {\alpha + k - 1 \choose k} (-1)^k$

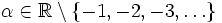Für $\alpha\in\mathbb R\setminus\{-1,-2,-3,\ldots\}$ erlaubt die Betafunktion B(x,y) eine Erweiterung der Definition auf reelle k:

${\alpha \choose k}=\frac{1}{(\alpha+1)\cdot\mathrm B(k+1,\alpha-k+1)}$

Ist dabei k oder α − k eine negative ganze Zahl, so ist der Wert der rechten Seite 0.

Weblinks

• Download von BigAl (Kleines, freies und plattformunabhängiges Programm, u. a. zur genauen Berechnung des Binomialkoeffizienten; mit Quelltext)
• Online-Berechnung beliebiger Binomialkoeffizienten
• Tool zur Online-Berechnung des Binomialkoeffizienten (benötigt kein JavaScript o.ä.)