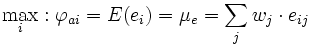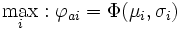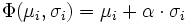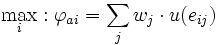Μ-Regel

Von einer Entscheidung unter Risiko spricht man im Rahmen der Entscheidungstheorie dann, wenn der Entscheidungsträger die Wahrscheinlichkeiten für das Eintreten der möglichen Umweltzustände kennt. Diese Wahrscheinlichkeiten können sowohl objektiv bekannt sein (Lotto, Roulette) oder auf subjektiven Schätzungen (z. B. aufgrund von Vergangenheitsdaten) beruhen.

Allgemeines

Entscheidung unter Risiko ist nach dem üblichen Sprachgebrauch ein Unterfall von Entscheidung unter Unsicherheit. Während man bei Kenntnis von Eintrittswahrscheinlichkeiten der Umweltzustände von Risiko spricht, liegt eine Entscheidung unter Ungewissheit vor, wenn man zwar die möglichen Umweltzustände kennt, jedoch keine Eintrittswahrscheinlichkeiten angeben kann.

Bei Entscheidungen unter Risiko liegt eine Ergebnismatrix vor, die das Entscheidungsproblem darstellt: Der Entscheider hat die Wahl zwischen verschiedenen Alternativen a_i, die abhängig von den möglichen Umweltzuständen s_j verschiedene Ergebnisse e_ij zur Folge haben. Die Wahrscheinlichkeiten w_j der verschiedenen Umweltzustände sind bekannt, wobei gilt: 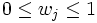$0 \le w_j \le 1$ und

∑	wj = 1
j

.

• Beispiel: 100 € sollen für ein Jahr angelegt werden. Zur Wahl stehen: eine Aktie (a₁) oder der Sparstrumpf, der keine Zinsen abwirft (a₂). Die möglichen Umweltzustände sind: Der Aktienkurs steigt (s₁), er sinkt (s₂) oder er bleibt gleich (s₃).

Die Ergebnismatrix sieht dann zum Beispiel wie folgt aus:

	s1	s2	s3
a1	120	80	100
a2	100	100	100
p	1/3	1/3	1/3

Der Entscheider rechnet mit einer Wahrscheinlichkeit von w₁ damit, dass der Aktienkurs steigt, mit einer Wahrscheinlichkeit von w₂ rechnet er mit einem Sinken des Aktienkurses und mit einer Wahrscheinlichkeit von w₃ bleibt der Kurs unverändert.

Entscheidungsregeln

Bei Entscheidungen unter Risiko können folgende Entscheidungsregeln Anwendung finden:

Die Bayes-Regel

Die Bayes-Regel wird auch μ-Regel genannt. Hierbei orientiert sich der Entscheider nur nach den Erwartungswerten.

$\max_i : \varphi{}_{ai} = E(e_i) = \mu{}_e = \sum_j w{}_j \cdot e_{ij}$

Da nur der Erwartungswert der jeweiligen Alternative a_i bewertet wird, ist der Entscheider risikoneutral, er ist beispielsweise indifferent hinsichtlich der Teilnahme an einer Lotterie per Münzwurf, in der er mit 50% Wahrscheinlichkeit 1 € gewinnt und mit 50% Wahrscheinlichkeit 1 € verliert. Im obigen Beispiel ist der dann indifferent, wenn gilt: e₁₁*w₁ + e₁₂*w₂ + e₁₃*w₃ = 100 (da unabhängig von den Wahrscheinlichkeiten w_j eine sichere "Auszahlung"), hier also: 120*w₁ + 80*w₂ + 100*w₃. Indifferenz würde z. B. vorliegen bei Gleichverteilung, wenn also gilt: w₁ = w₂ = w₃ = $\frac{1}{3}$.

Probleme bei Erwartungswerten

Das Beispiel des Petersburger Paradoxons zeigt, dass die Berücksichtigung von Erwartungswerten nicht dem Entscheidungsverhalten von Menschen in der Realität entspricht:

• Eine (ideale) Münze (d.h. Kopf und Zahl erscheinen jeweils mit einer Wahrscheinlichkeit von 50%) wird geworfen.
• Der Spieler erhält als Auszahlung:
  • 2 €, wenn bereits beim ersten Wurf Kopf erscheint
  • 4 €, wenn erst beim zweiten Wurf Kopf erscheint
  • ...
  • 2ⁿ €, wenn erst beim n-ten Wurf Kopf erscheint
• Der Preis der Lotterie soll ein fairer Preis sein, d.h. dem Erwartungswert entsprechen.

Ein Entscheider, der nur nach dem Erwartungswert entscheidet, wäre jetzt also bereit, für die Teilnahme an dieser Lotterie diesen fairen Preis, also den Erwartungswert zu zahlen (er wäre dann genau indifferent zwischen der Teilnahme und der Nicht-Teilnahme):

Der Erwartungswert ermittelt sich wie folgt:

• Die Wahrscheinlichkeit, dass beim ersten Wurf Kopf erscheint ist genau ${1 \over2}$, die Auszahlung ist 2.
• Die Wahrscheinlichkeit, dass beim zweiten Wurf Kopf erscheint ist genau ${1 \over4}$, die Auszahlung ist 4.
• ...
• Die Wahrscheinlichkeit, dass beim n-ten Wurf Kopf erscheint ist genau 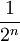$\frac{1}{2^n}$, die Auszahlung ist 2ⁿ.

Also ist 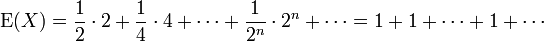$\operatorname{E}(X) ={1 \over2} \cdot 2 + {1 \over4} \cdot 4 + \dotsb + \frac{1}{2^n} \cdot 2^n + \dotsb = 1 + 1 + \dotsb + 1 + \dotsb$, also unendlich.

In der Realität ist jedoch niemand bereit, unendlich viel Geld für die Teilnahme an der Lotterie zu zahlen.

Die μ-σ-Regel

In der μ-σ-Regel findet die Risikoeinstellung des Entscheiders dadurch Berücksichtigung, dass auch die Standardabweichung berücksichtigt wird. Bei risikoneutralen Entscheidern entspricht sie der Bayes-Regel, bei risikoaversen (risikoscheuen) Entscheidern sinkt die Attraktivität einer Alternative a_i mit zunehmender Standardabweichung. Bei risikofreudigen Entscheidern steigt die Attraktivität hingegen.

$\max_i : \varphi_{ai} = \Phi ( \mu_i, \sigma_i )$

Eine mögliche Form der μ-σ-Regel ist zum Beispiel:

$\Phi ( \mu_i, \sigma_i ) = \mu_i + \alpha \cdot \sigma_i$

Für α > 0 gilt: Der Entscheider ist risikofreudig, eine Alternative mit einem höheren σ wird einer Alternative mit gleichem Erwartungswert μ aber niedrigerem σ vorgezogen. Für α < 0 gilt: Der Entscheider ist risikoavers, eine Alternative mit niedrigerem σ wird einer Alternative mit gleichem Erwartungswert, aber höherem σ vorgezogen. Für α = 0 entspricht die Regel der Bayes-Regel, der Entscheider ist risikoneutral, die Standardabweichung σ hat keinen Einfluss auf die Bewertung der Alternativen.

Als Voraussetzung für die Anwendung der μ-σ-Regel gelten im Allgemeinen normalverteilte zukünftige Renditen oder eine quadratische Nutzenfunktion.

Das Bernoulli-Prinzip

Bei der Anwendung des Bernoulli-Prinzips müssen die Ergebnisse e_ij erst mit Hilfe einer Risikonutzenfunktion in Nutzenwerte umgewandelt werden. Die individuelle Risikonutzenfunktion u(e_ij) spiegelt dabei die Risikoeinstellung des Entscheiders wider. Eine Risikonutzenfunktion, die eine konkave Funktion ist, steht dabei für einen risikoaversen Entscheider, während eine konvexe Funktion einen risikofreudigen Entscheider abbildet. Es ist dabei allerdings möglich, dass die Risikonutzenfunktion sowohl konkave als auch konvexe Bereiche aufweist. Dies bildet zum Beispiel die empirisch beobachtbare Tatsache ab, dass Menschen sowohl Lotto spielen (Risikofreude), als auch Versicherungen abschließen (Risikoaversion).

Maximiert wird dabei der Erwartungswert der Risikonutzenfunktion.

$\max_i : \varphi_{ai} = \sum_j w_j \cdot u(e_{ij})$

Das Bernoulli-Prinzip ist im eigentlichen Sinne keine Entscheidungsregel, sondern nur ein Entscheidungsprinzip, da unter Umständen eine eindeutige Festlegung der Entscheidung nicht möglich ist.

Siehe auch

• Entscheidung unter Sicherheit
• Entscheidung unter Unsicherheit
• Erwartungsnutzentheorie