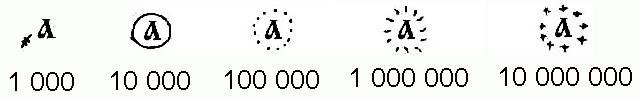҂

Die kyrillischen Zahlen sind ein Zahlensystem, das auf den kyrillischen Buchstaben beruht. Es wird bei den Süd- und Ostslawen in vor allem kirchenslawischen Texten benutzt, die in alter Kyrilliza geschrieben sind. Seit dem 16. Jahrhundert wurden daneben auch arabische und römische Zahlen benutzt. In der von Peter dem Großen 1708 eingeführten bürgerlichen Schrift werden kyrillische Zahlen nicht mehr verwendet.

Zahlenwerte der kyrillischen Buchstaben

Das kyrillische Zahlensystem ist ein Additionssystem, in dem insgesamt 27 Buchstaben für die Zahlen bis neun (1, 2, … 9), die Vielfachen von zehn (10, 20, … 90) und die Vielfachen von hundert (100, 200, … 900) stehen.

Dieses System basiert direkt auf dem milesischen Typ der griechischen Zahlen. Daher haben alle kyrillischen Buchstaben den Zahlenwert der ihnen entsprechenden griechischen Buchstaben. Die bereits im Griechischen obsoleten Buchstaben Stigma/Digamma, Koppa und Sampi, die dort nur noch als Zahlzeichen im Gebrauch waren, wurden durch nicht auf das Griechische zurückgehende kyrillische Buchstaben ersetzt, die diesen äußerlich ähnlich sahen. Alle anderen spezifisch slawischen Buchstaben (б, ж, ш, щ usw.) haben also keinen Zahlenwert.

Um anzuzeigen, dass die Buchstaben nicht als Lautwerte, sondern als Zahlen gelesen werden sollen, wird Titlo über die Zahl gesetzt (manchmal auch über jedes einzelne Zahlzeichen). (Im Griechischen steht in dieser Funktion ein Apostroph hinter der Zahl.) Oft wird eine Zahl zusätzlich in Punkte eingeschlossen.

Wert griechisch kyrillisch 1 αʹ а҃ 2 βʹ в҃ 3 γʹ г҃ 4 δʹ д҃ 5 εʹ е҃ 6 ϛʹ oder ϝʹ ѕ҃ 7 ζʹ з҃ 8 ηʹ и҃ 9 θʹ ѳ҃

Wert griechisch kyrillisch 10 ιʹ і҃ 20 κʹ к҃ 30 λʹ л҃ 40 μʹ м҃ 50 νʹ н҃ 60 ξʹ ѯ҃ 70 οʹ о҃ 80 πʹ п҃ 90 ϟʹ ч҃

Wert griechisch kyrillisch 100 ρʹ р҃ 200 σʹ с҃ 300 τʹ т҃ 400 υʹ ѵ҃ 500 φʹ ф҃ 600 χʹ х҃ 700 ψʹ ѱ҃ 800 ωʹ ѡ҃ 900 Ϡʹ ц҃ oder ѧ҃

Eine Gegenüberstellung der teilweise voneneinander abweichenden kyrillischen und glagolitischen Zahlenwerte der Buchstaben enthält der Artikel „Glagolitische Zahlen“.

Kombination der Zahlzeichen

Zahlen, die größer als 10 und nicht durch 10 teilbar sind, werden geschrieben, indem man die Zahlzeichen zu einer Summe kombiniert, also z. B. 23 = 20 + 3 (kyrillisch ·кг҃·) oder 735 = 700 + 30 + 5 (·ѱл҃е·). „Nullen“ werden dabei (ähnlich wie bei den römischen Zahlen) ausgelassen, also z. B. 705 = 700 + 5 (·ѱе҃·).

Dabei werden die Zeichen in der Regel von links nach rechts in absteigender Größe geschrieben. Eine Besonderheit ist jedoch, dass die Zahlen von 11 bis 19 entsprechend der Reihenfolge beim Sprechen „rückwärts“ geschrieben werden, also 113 = 100 + 3 + 10 (·рг҃і·) gemäß der Aussprache als sъto tri na desęti ‘hundert drei auf zehn’ (vgl. dt. hundert-drei-zehn). Die Zahlen ab 21 werden hingegen entgegen dem Deutschen in der „logischen“ Reihenfolge gesprochen und geschrieben, z. B. 123: sъto dъvě desęti tri ‘hundert zwei-zehn drei’ (vgl. engl. a hundred and twenty-three), also 100 + 20 + 3 (·рк҃г·).

Zahlen ab 1000

Da es keine Zahlzeichen für Tausender gibt, ist die höchste mit diesem System darstellbare Zahl 999 (900 + 90 + 9, ·цч҃ѳ·). Für Zahlen ab 1000 wird daher ein Tausendzeichen (҂) vor einen Buchstaben geschrieben, das anzeigt, dass der Zahlenwert des folgenden Buchstaben mit 1000 zu multiplizieren ist, also ҂а = 1000, ҂в = 2000 usw. (Im Griechischen steht hier eine Art Komma vor der Zahl, also ͵α, ͵β usw.)

Beispiele:

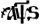• = ·҂аѱ҃ѕ· = 1706
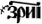• = ·҂зри҃і· = 7118 (entspricht als Jahr seit der Schöpfung nach der byzantinischen Ära dem Jahr 1610 n. Chr.)

Auf diese Art und Weise lassen sich auch höhere Zahlen darstellen, z. B. ·҂к҃· = 20 000 oder auch ·҂ц҂ч҂ѳ҃цчѳ· = 999 999. Daneben gibt es aber auch weitere Schreibweisen zur Darstellung von Zehnerpotenzen:^[1]

Quellen

1. ↑ Vgl. Vjačeslav Nikolaevič Ščepkin, Russkaja paleografija, Moskva ³1999 (¹1918), S. 165.

Siehe auch

• Kyrillisches Alphabet

• Glagolitische Zahlen
• Griechische Zahlen
• Hebräische Zahlen
• Arabische Buchstabenzahlen
• Armenische Zahlen

Zahlensysteme

Ägyptisch | Arabisch | Armenisch | Attisch | Babylonisch | Brahmi | Chinesisch | Etruskische | Glagolitisch | Griechisch | Hebräisch | Indisch | Japanisch | Khmer | Koreanisch | Kyrillisch | Maya | Römisch | Sanskrit | Thai