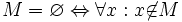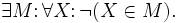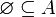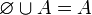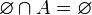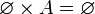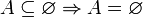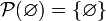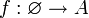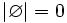∅

{ }

∅

Die leere Menge ist ein grundlegender Begriff aus der Mengenlehre. Man bezeichnet damit die Menge, die keinerlei Elemente enthält. Da Mengen über ihre Elemente charakterisiert werden und zwei Mengen genau dann gleich sind, wenn sie dieselben Elemente haben, gibt es nur eine einzige leere Menge.

Notation

Als Zeichen für die leere Menge hat sich das von Nicolas Bourbaki verwendete Zeichen 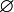$\varnothing$ (ein durchgestrichener Kreis) weitgehend durchgesetzt. Eine typographische Variante davon ist 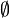$\emptyset$ (eine durchgestrichene Null).

Als typographischer Ersatz dient oft auch der skandinavische Buchstabe "Ø": ø oder Ø (ein durchgestrichenes o bzw. O), manchmal – wegen des ähnlichen Aussehens – auch 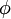$\;\phi$, eine Variante des griechischen Buchstabens „φ“, mit dem es jedoch nicht verwechselt werden sollte. Im Unicode-Standard schließlich gibt es das Zeichen ∅ (U+2205, Bezeichnung „Empty set“), das nicht mit dem Unicode-Zeichen für Durchmesser ⌀ (U+2300) verwechselt werden sollte. In manchen älteren Büchern wird auch 0 (Null) verwendet.

Alternativ kann man die leere Menge durch leere Mengenklammern notieren: $\{\,\}$

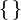
Definition (formal)

Eine Menge M ist genau dann die leere Menge, wenn für jedes denkbare Objekt gilt, dass es nicht Element von M ist. Formal schreibt sich das zu

$M = \varnothing \Leftrightarrow \forall x : x \not\in M$

Axiomatik

Die heutzutage meistgenutzte axiomatische Basis der Mengenlehre, die Zermelo-Fraenkel-Mengenlehre, postuliert die Existenz der leeren Menge im zweiten Axiom, und wurde von Ernst Zermelo schon 1907 in der ursprünglichen Version in dem Elementarmengenaxiom aufgeführt.

Das Axiom lautet:

Es gibt eine Menge, die nichts enthält.

Die gleichwertige logische Formulierung lautet

Es existiert eine Menge, die von allem was existiert, nichts enthält:

$\exist M\colon \forall X\colon \lnot (X \in M).$

Die Eindeutigkeit lässt sich dann leicht aus dem ersten Axiom folgern, dem Extensionalitätsaxiom.

Eigenschaften

• Die leere Menge ist Teilmenge jeder Menge:

$\varnothing \subseteq A$

• Jede Menge bleibt bei Vereinigung mit der leeren Menge unverändert:

$\varnothing \cup A = A$

• Für jede Menge ist der Durchschnitt mit der leeren Menge die leere Menge:

$\varnothing \cap A = \varnothing$

• Für jede Menge ist das kartesische Produkt mit der leeren Menge die leere Menge:

$\varnothing \times A =\varnothing$

• Die einzige Teilmenge der leeren Menge ist die leere Menge:

$A \subseteq \varnothing \Rightarrow A = \varnothing$

• Daraus folgt, dass die Potenzmenge der leeren Menge genau ein Element enthält, nämlich die leere Menge selbst:

$\mathcal P(\varnothing) = \left\{ \varnothing \right\}$

• Für jede widersprüchliche Aussage oder nicht erfüllbare Eigenschaft E(x) gilt:

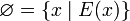$\varnothing = \left\{ x \mid E(x) \right\}$, z.B.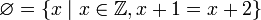 $\varnothing = \left\{ x \mid x \in \mathbb Z, x+1=x+2 \right\}$

• Jede Existenzaussage über Elemente einer Menge, etwa

  Es existiert ein x aus A, sodass gilt... ist für die leere Menge falsch

• Analog sind Aussagen über alle Elemente einer Menge, z. B.

  „für alle Elemente der Menge gilt…“ für die leere Menge immer wahr, denn es gibt keine Elemente, für die die fragliche Eigenschaft nachgeprüft werden müsste.

• Für jede Menge A gibt es genau eine Abbildung

$f : \varnothing \to A$

• Die leere Menge ist definitionsgemäß in jedem topologischen Raum zugleich abgeschlossen und offen.

Kardinalität der leeren Menge

Die leere Menge ist die einzige Menge mit der Mächtigkeit Null:

$\left\vert \varnothing \right\vert = 0$

Sie ist daher auch der einzige Repräsentant der Kardinalzahl 0 und der Ordinalzahl 0. Insbesondere ist sie eine endliche Menge.