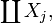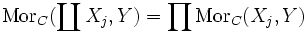∐

Im mathematischen Teilgebiet der Kategorientheorie ist der Begriff des Koproduktes eine Verallgemeinerung der so genannten disjunkten Vereinigung von Mengen.

Definition

Diagramm zum Koprodukt

Sind X_j Objekte einer Kategorie C, so heißt ein Objekt X zusammen mit Morphismen 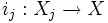$i_j: X_j \rightarrow X$ Koprodukt der X_j, geschrieben

$\coprod X_j,$

falls die folgende universelle Eigenschaft erfüllt ist:

Für jedes Objekt Y von C und Morphismen 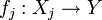$f_j: X_j \rightarrow Y$ gibt es genau einen Morphismus 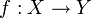$f:X \rightarrow Y$, so dass 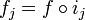$f_j=f\circ i_j$ für alle j gilt.

Äquivalent dazu kann man fordern, dass

$\mathrm{Mor}_C(\coprod X_j,Y)=\prod\mathrm{Mor}_C(X_j,Y)$

gilt; dabei vermitteln die i_j die natürliche Äquivalenz.

Beispiele

Kategorie	Koprodukt
Mengen	disjunkte Vereinigung
Gruppen	freies Produkt
Vektorräume	direkte Summe
abelsche Gruppen
Moduln über einem Ring
topologischen Räume	disjunkte Vereinigung mit der offensichtlichen Topologie
kommutative Ringe mit Einselement	Tensorprodukt