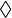⋄

$\Diamond$ (Karo) ist ein "kombinatorisches" Prinzip in der Mengenlehre.

Definition

Für jede unendliche Kardinalzahl κ ist 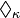$\Diamond_\kappa$ eine Abkürzung für die folgenden Aussage:

• es gibt eine Folge 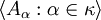$\langle A_\alpha: \alpha \in \kappa \rangle$ mit folgenden Eigenschaften:

• für alle α gilt $A_\alpha \subseteq \alpha$
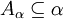
• für alle 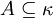$A \subseteq \kappa$ ist die Menge $\{\alpha \in \kappa : A \cap \alpha = A_\alpha\}$ ein stationäre Teilmenge von κ.

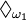Statt $\Diamond_{\omega_1}$ schreibt man oft nur $\Diamond$.

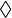Zusammenhang mit CH und GCH

Man zeigt leicht, dass aus ◊ die Kontinuumshypothese CH folgt. Allgemeiner folgt aus 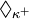$\Diamond_{\kappa^+}$ die Gleichung 2^κ = κ ⁺ . Aus CH kann man ◊ nicht folgern, aber aus 2^κ = κ ⁺ zusammen mit κ^ω = κ kann man 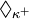$\Diamond_{\kappa^+}$ schließen. Aus der verallgemeinerten Kontinuumshypothese GCH folgt also 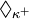$\Diamond_{\kappa^+}$ für alle κ mit überabzählbarer Konfinalität.

Anwendungen

Mit Hilfe von ◊ kann man eine Suslingerade konstruieren.