- Besondere Zahlen
-
Besondere Zahlen sind zum einen Zahlen, die im Sinne der Zahlentheorie eine oder mehrere auffällige Eigenschaften besitzen. Außerdem haben viele Zahlen eine besondere Bedeutung in der Mathematik und/oder in Bezug auf die reale Welt. Diese letzteren Zahlen werden im zweiten Teil dieses Artikels aufgelistet.
Inhaltsverzeichnis
Zahlen mit besonderen Eigenschaften
Bis 0
- −2
- Kleinste ganze Zahl d, für die der Ring
![\mathbb{Z}[\sqrt{d}]](/pictures/dewiki/99/cec8ff0291d248b3c45dbc823e14e8e9.png) euklidisch ist.
euklidisch ist. - Größte triviale Nullstelle der Zetafunktion ζ( − 2) = 0.
- −1
- Eine Einheit im Primring der ganzen Zahlen sowie seinen Erweiterungsringen.
- Die größte negative ganze Zahl.
- Einzige komplexe Zahl der multiplikativen Ordnung 2.
- Jede reelle Zahl lässt sich als Produkt aus −1 und ihrem Negativen darstellen.
- Im Körper der komplexen Zahlen ist − 1 = i2
- −0,5
- Funktionswert der Zetafunktion ζ(0)
- −0,083333333333333…
- Funktionswert der Zetafunktion
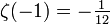
- 0
- Neutrales Element der Addition im Primring der ganzen Zahlen sowie seiner Erweiterungsringe. (Das sind u. a. die Körper der rationalen, der reellen und der komplexen Zahlen.)
- Die Ziffer 0 ermöglicht unser Stellenwertsystem.
Bis 1
- 0,0112359550561797… (Folge A021093 in OEIS)
- =
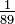 ist der Wert der unendlichen Reihe
ist der Wert der unendlichen Reihe 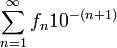 , deren Summanden jeweils das Produkt aus der n-ten Fibonacci-Zahl fn mit 10 − (n + 1) sind.
, deren Summanden jeweils das Produkt aus der n-ten Fibonacci-Zahl fn mit 10 − (n + 1) sind.
- =
- 0,2078795763507619… (Folge A049006 in OEIS)
- = ii: Die imaginäre Einheit i zur Potenz i hat den reellen Wert e − π / 2 (siehe auch eulersche Identität) (gilt allerdings nur bei nicht-kanonischer Wahl eines Zweiges des komplexen Logarithmus).
- 0,2247448713915890…
- =
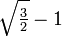 : relativer Abstand der optimalen Auflagenpunkte von den Rändern eines gleichmäßig belasteten Balkens (Bessel-Punkte).
: relativer Abstand der optimalen Auflagenpunkte von den Rändern eines gleichmäßig belasteten Balkens (Bessel-Punkte).
- =
- 0,3678794411714423… (Folge A068985 in OEIS)
- = 1/e: Minimalstelle der Funktion f(x) = xx, da 1 / e Nullstelle von
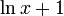 und
und 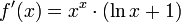
- = 1/e: Minimalstelle der Funktion f(x) = xx, da 1 / e Nullstelle von
- 0,4142135623730950… (Folge A014176 in OEIS)
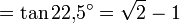 algebraischer Wert der Tangensfunktion für halbzahliges Argument im Gradmaß
algebraischer Wert der Tangensfunktion für halbzahliges Argument im Gradmaß
- 0,5772156649015328… (Folge A001620 in OEIS)
- 0,6180339887498948… (Folge A094214 in OEIS)
- Kehrwert des Goldenen Schnitts
 und zugleich der um eins verringerte Goldene Schnitt:
und zugleich der um eins verringerte Goldene Schnitt: 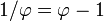
- Kehrwert des Goldenen Schnitts
- 0,6922006275553463… (Folge A072364 in OEIS)
- =
![(1/e)^{1/e} =\sqrt[-e]{e}](/pictures/dewiki/98/b75a72cdb5d60bb3ea04e33c61811cd6.png) Minimalwert der Funktion f(x) = xx:
Minimalwert der Funktion f(x) = xx: 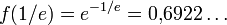
- =
- 0,8660254037844386… (Folge A010527 in OEIS)
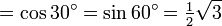 algebraischer Wert der Kosinusfunktion für ganzzahliges Argument im Gradmaß
algebraischer Wert der Kosinusfunktion für ganzzahliges Argument im Gradmaß
- 0,8705883…
- Brunsche Konstante B4 (Summe der Kehrwerte aller Primzahlvierlinge)
- 0,9159655941772190… (Folge A006752 in OEIS)
- 1
- neutrales Element der Multiplikation im Primring der ganzen Zahlen sowie seinen Erweiterungsringen (das sind u. a. die Körper der rationalen, der reellen und der komplexen Zahlen).
- Kleinste positive ganze Zahl.
Bis 10
- 1,0173430619844491… (Folge A013664 in OEIS)
- Funktionswert der Zetafunktion ζ(6) = π6 / 945
- 1,0823232337111381… (Folge A013662 in OEIS)
- Funktionswert der Zetafunktion ζ(4) = π4 / 90
- 1,2020569031595942… (Folge A002117 in OEIS)
- Apéry-Konstante und damit ζ(3) der riemannschen Zetafunktion
- 1,2618595071429148… (Folge A100831 in OEIS)
- Hausdorff-Dimension der Koch-Kurve, log34
- 1,4142135623730950… (Folge A002193 in OEIS)
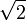 , d. h. die Quadratwurzel aus zwei (Wurzel 2).
, d. h. die Quadratwurzel aus zwei (Wurzel 2).- Wert der Länge der Diagonale eines Quadrats mit der Seitenlänge eins.
- 1,6180339887498948… (Folge A001622 in OEIS)
- 1,6449340668482264… (Folge A013661 in OEIS)
- Funktionswert der Zetafunktion ζ(2) = π2 / 6
- 1,7320508075688772… (Folge A002194 in OEIS)
- 1,90216058… (Folge A065421 in OEIS)
- Brunsche Konstante B2 (Summe der Kehrwerte aller Primzahlzwillinge)
- 2
- Kleinste Primzahl.
- Ordnung des kleinsten Körpers.
- Es ist die 2. Catalan-Zahl.
- Kleinste Basis eines Stellenwertsystems, des Dualsystems.
- Außerdem gilt
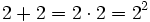
- 2,4142135623730950… (Folge A014176 in OEIS)
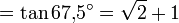 algebraischer Wert der Tangensfunktion für halbzahliges Argument im Gradmaß
algebraischer Wert der Tangensfunktion für halbzahliges Argument im Gradmaß
- 2,5029078750958928… (Folge A006891 in OEIS)
- Eine der beiden Feigenbaum-Konstanten
- 2,6220575542921198… (Folge A062539 in OEIS)
- Lemniskatische Konstante
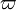 , definiert als der Wert des elliptischen Integrals
, definiert als der Wert des elliptischen Integrals
- Lemniskatische Konstante
- 2,7182818284590452… (Folge A001113 in OEIS)
- 3
- Kleinste ungerade Primzahl.
- Fermat-Zahl F0.
- Mersenne-Primzahl M2.
- Kleinste natürliche Zahl, die nicht als Funktionswert der eulerschen φ-Funktion auftritt.
- 3,1415926535897932… (Folge A000796 in OEIS)
- Kreiszahl π, Verhältnis des Umfangs eines Kreises zu seinem Durchmesser.
- 4
- Kleinste zusammengesetzte Zahl.
- Anzahl der Farben, die ausreicht um eine beliebige ebene Landkarte zu färben (Vier-Farben-Satz).
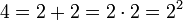 .
.- Anzahl der Flächen und der Ecken eines Tetraeders.
- Kleinste natürliche Zahl n, für die sich jede nichtnegative ganze Zahl als Summe von höchstens n Quadratzahlen darstellen lässt (siehe: Waringsches Problem).
- Punktanzahl der kleinsten affinen Ebene.
- Ordnung des kleinsten nicht kommutativen Rings ohne Einselement.
- Maximaler Grad algebraischer Gleichungen, die mit Hilfe von Wurzelziehen zu lösen sind.
- 4,6692016091029906… (Folge A006890 in OEIS)
- Feigenbaum-Konstante: Fixpunkt der logistischen Gleichung, Übergang ins Chaos.
- 5
- Anzahl der platonischen Körper.
- Kleinste positive natürliche Zahl, deren Quadrat sich als Summe von zwei positiven Quadratzahlen schreiben lässt: 52 = 32 + 42 (siehe auch: pythagoreisches Tripel).
- Fermat-Zahl F1.
- Größte Eckenzahl eines regelmäßigen Polygons, das als Seitenfläche eines platonischen Körpers auftritt.
- Bestandteil der beiden Primzahl-Zwillinge (3;5) und (5;7).
- Kleinste Wilson-Primzahl.
- Kleinste mögliche Mirpzahl (im Dreiersystem ist die dezimale 5 12, die dezimale 7 21).
- Die 3. Catalan-Zahl.
- 6
- Kleinste vollkommene oder ideale Zahl.
- Die Summe ist gleich dem Produkt der echten Teiler: 6 = 1 + 2 + 3 = 1 · 2 · 3
- Flächenanzahl des Würfels.
- Eckenanzahl des Oktaeders.
- Kantenanzahl des Tetraeders.
- In der Ebene kann ein Kreis von maximal 6 weiteren Kreisen gleicher Größe so berührt werden, dass keine Überlappungen auftreten.
- Kleinste positive natürliche Zahl, deren dritte Potenz sich als Summe von 3 positiven Kubikzahlen schreiben lässt: 63 = 33 + 43 + 53.
- Größte Ordnung, zu der kein griechisch-lateinisches Quadrat existiert.
- Ordnung der kleinsten nicht-abelschen Gruppe S3.
- Kleinste natürliche Zahl, die keine Primzahlpotenz ist.
- Kleinste natürliche Zahl n größer als 1, zu der kein Körper der Ordnung n existiert.
- Kleinste primär pseudovollkommene Zahl.
- Form jeder Schneeflocke ist immer sechseckig. Wegen der besonderen Struktur der Wassermoleküle sind dabei nur Winkel von 60° bzw. 120° möglich.
- 7
- Kleinste Eckenzahl eines regelmäßigen Vielecks, das nicht mit Zirkel und Lineal konstruierbar ist.
- Mersenne-Primzahl M3.
- Anzahl der Farben, die ausreicht um eine beliebige Landkarte auf einem Torus zu färben.
- Kleinste nichtnegative ganze Zahl, die sich nicht als Summe von weniger als vier Quadratzahlen schreiben lässt (siehe: Waringsches Problem).
- Anzahl der Punkte und Geraden der kleinsten projektiven Ebene, der Fano-Ebene.
- Kleinste positive natürliche Zahl n, für die n Rechtecke paarweise verschiedener positiver Kantenlängen existieren, die sich zu einem Rechteck zusammensetzen lassen.
- 8
- Flächenanzahl des Oktaeders und Eckenanzahl des Würfels.
- Größte Fibonacci-Zahl, die gleichzeitig eine Kubikzahl ist.
- Ordnung des kleinsten nicht kommutativen unitären Rings.
- 9
- Kleinste ungerade zusammengesetzte Zahl.
- Kleinste natürliche Zahl n, für die sich jede nichtnegative ganze Zahl als Summe von höchstens n positiven Kubikzahlen darstellen lässt (siehe: waringsches Problem).
- Kleinste positive natürliche Zahl n, für die n Quadrate paarweise verschiedener positiver Kantenlänge existieren, die sich zu einem Rechteck zusammensetzen lassen. **Ordnung der kleinsten nicht desarguesschen projektiven Ebene.
- 10
- Größte Eckenzahl eines regelmäßigen Polygons, das als Seitenfläche eines archimedischen Körpers auftritt.
- Kleinste natürliche Zahl a, für die
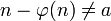 für alle natürlichen Zahlen n gilt (
für alle natürlichen Zahlen n gilt ( ist die eulersche φ-Funktion).
ist die eulersche φ-Funktion).
Bis 100
- 11
- Länge des Golay-Codes G11, des einzigen nichttrivialen perfekten ternären Codes, der mehr als einen Fehler korrigieren kann.
- Kleinste Primzahl p, für die 2p − 1 keine Mersenne-Primzahl ist.
- Kleinste Repunit-Primzahl[1]
- 12
- Kleinste abundante Zahl.
- Flächenanzahl des Dodekaeders, Kantenanzahl des Würfels und des Oktaeders, Eckenanzahl des Ikosaeders.
- 1. erhabene Zahl und einzige unter 1 Billion
- 3. Fünfeckszahl
- 4. Rechteckzahl
- Ordnung der Drehgruppe A4 des Tetraeders.
- 13
- Anzahl der archimedischen Körper, wenn nicht zwischen ähnlichen Körpern unterschieden wird. Zweite Wilson-Primzahl. kleinste Mirpzahl im Dezimalsystem
- 14
- Anzahl der Bravais-Gitter.
- Kleinste gerade natürliche Zahl, die nicht als Funktionswert der eulerschen φ-Funktion auftritt.
- Es ist die 4. Catalan-Zahl.
- 14,134725141734693…
- Imaginärteil der betragsmäßig kleinsten nichttrivialen Nullstelle
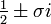 der Zetafunktion
der Zetafunktion
- Imaginärteil der betragsmäßig kleinsten nichttrivialen Nullstelle
- 15
- Anzahl der archimedischen Körper, wenn nicht-spiegelungsinvariante Körper doppelt gezählt werden.
- Kleinste zusammengesetzte Zahl n, für die bis auf Isomorphie nur eine einzige Gruppe der Ordnung n existiert.
- Kleinste Pseudoprimzahl. Kleinste natürliche Zahl, die sich nicht als Summe von weniger als acht Kubikzahlen schreiben lässt (siehe: Waringsches Problem).
- 16
- 16 = 24 = 42, damit ist 16 die einzige Zahl n, für die voneinander verschiedene natürliche Zahlen 'a und b existieren mit n = ab = ba.
- Kleinste natürliche Zahl n, so dass sich bis auf endlich viele Ausnahmen jede natürliche Zahl als Summe von höchstens n Biquadraten schreiben lässt (siehe: Waringsches Problem).
- Ordnung des kleinsten, nicht zu sich selbst antiisomorphen unitären Rings.
- 17
- Fermat-Zahl F2.
- Anzahl der kristallografischen Gruppen in der Ebene.
- Gauß hielt die Konstruktion des regelmäßigen 17-Ecks mit Zirkel und Lineal für eine seiner wichtigsten Entdeckungen.
- 18
- Das erste Maximum der Anzahl nicht-isomorpher kubischer Käfiggraphen gegebener Taillenweite ν, das mit wachsender Taillenweite dieser Graphen bei ν = 9 erreicht wird.
- 19
- Kleinste natürliche Zahl n, für die sich jede positive natürliche Zahl als Summe von höchstens n Biquadraten darstellen lässt (siehe: Waringsches Problem).
- Größte ganze Zahl d, für die der Ring
![\mathbb{Z}[\sqrt{d}]](/pictures/dewiki/99/cec8ff0291d248b3c45dbc823e14e8e9.png) euklidisch ist.
euklidisch ist.
- 20
- Flächenanzahl des Ikosaeders und Eckenanzahl des Dodekaeders.
- 21
- Kleinste positive natürliche Zahl n, für die n Quadrate paarweise verschiedener positiver Kantenlänge existieren, die sich zu einem Quadrat zusammensetzen lassen.
- 22
- Der erste Koeffizient der Kettenbruch-Darstellung von πe.
- 23
- Kleinste positive natürliche Zahl n, für die n Quader paarweise verschiedener positiver Kantenlänge existieren, die sich zu einem Quader zusammensetzen lassen.
- Kleinste und neben der 239 einzige natürliche Zahl, die sich nicht als Summe von weniger als 9 Kubikzahlen schreiben lässt (siehe Waringsches Problem).
- Länge des Golay-Codes G23, dem einzigen nichttrivialen perfekten binären Code, der mehr als einen Fehler korrigieren kann.
- 24
- Ordnung der Drehgruppe S4 des Würfels und des Oktaeders.
- Größte natürliche Zahl n mit der Eigenschaft, dass alle natürlichen Zahlen kleiner als
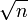 Teiler von n sind.
Teiler von n sind.
- 25
- Kleinste Quadratzahl, die Summe zweier Quadratzahlen ist: 32 + 42 = 52 = 25
- 26
- Anzahl der sporadischen Gruppen
- einzige Zahl die in den natürlichen Zahlen jeweils benachbart zwischen einer Quadrat- und einer Kubikzahl liegt;
- 27
- Die kleinste natürliche Zahl, die auf zwei verschiedene Arten als Summe von drei Quadratzahlen geschrieben werden kann, nämlich als 32 + 32 + 32 = 52 + 12 + 12.
- 28
- Zweite vollkommene Zahl.
- 29
- Kleinste Primzahl, die Summe dreier aufeinanderfolgender Quadratzahlen ist: 22 + 32 + 42 = 29
- 30
- Kantenanzahl des Dodekaeders und des Ikosaeders.
- Flächenzahl des Rhombentriakontaeders. Kleinste Giuga-Zahl.
- Die größte natürliche Zahl n mit der Eigenschaft, dass alle natürlichen Zahlen kleiner als n, die zu n teilerfremd sind, Primzahlen sind.
- 31:
- 32
- Anzahl der Kristallklassen im dreidimensionalen Kristallgitter
- 33
- Die größte natürliche Zahl n, die sich nicht als Summe von zwei Dreieckszahlen darstellen lässt.
- 34
- Die kleinste Zahl, die die gleiche Teileranzahl wie ihr Vorgänger und ihr Nachfolger hat.
- 37
- Kleinste natürliche Zahl n, für die sich jede nichtnegative ganze Zahl als Summe von höchstens n fünften Potenzen nichtnegativer ganzer Zahlen darstellen lässt (siehe: Waringsches Problem).
- Kleinste irreguläre Primzahl.
- 41
- Das Polynom n2 + n + a liefert für a = 41 für alle
 Primzahlen.
Primzahlen.
- Das Polynom n2 + n + a liefert für a = 41 für alle
- 42
- Zweite primär pseudovollkommene Zahl.
- Die fünfte Catalan-Zahl.
- 50
- 50 = 52 + 52 = 72 + 12, damit ist 50 die kleinste positive Zahl, die sich auf mehr als eine Art als Summe von zwei positiven Quadratzahlen darstellen lässt.
- 60
- Die Ordnung der Ikosaedergruppe A5, also der kleinsten nicht-auflösbaren Gruppe und der kleinsten nicht-abelschen einfachen Gruppe.
- Die kleinste natürliche Zahl, die durch alle Zahlen von 2 bis 6 geteilt wird.
- Eckenanzahl von vier archimedischen Körpern: des Abgestumpften Dodekaeders, des Abgestumpften Ikosaeders oder Fussballkörpers, des Kleinen Rhombenikosidodekaeders und des Abgeschrägten Dodekaeders (Dodekaedron simum).
- Kantenanzahl von zwei archimedischen Körpern: des Ikosidodekaeders und des Abgeschrägten Würfels (Cubus simus).
- 70
- Kleinste weirde Zahl (zu deutsch „merkwürdig“).
- 71
- Größte supersinguläre Primzahl. Größte rechtsstutzbare Primzahl zur Basis 3.
- 72
- Kleinste positive natürliche Zahl, deren fünfte Potenz sich als Summe von fünf fünften Potenzen positiver natürlicher Zahlen schreiben lässt: 725 = 195 + 435 + 465 + 475 + 675.
- 79
- Kleinste natürliche Zahl, die sich nicht als Summe von weniger als 19 Biquadraten schreiben lässt (siehe: Waringsches Problem).
- 85
- 85 lässt sich auf zwei verschiedene Arten als Summe zweier Quadratzahlen darstellen: 85 = 9²+2²=7²+6²
Bis 1000
- 105
- Das Kreisteilungspolynom Φ105 ist das erste, dessen Koeffizienten nicht alle −1, 0 oder 1 lauten.
- 107
- Kleinste dreistellige Mirpzahl.
- 108
- Winkel des regelmäßigen Fünfecks
- 109,47…
- Tetraeder-Winkel
- 111
- Zweitkleinste Repunitzahl
- 127
- Mersenne-Primzahl M7. 27 - 1
- 132
- Sechste Catalan-Zahl.
- 144
- Kleinste positive natürliche Zahl, deren fünfte Potenz sich als Summe von 4 fünften Potenzen positiver natürlicher Zahlen schreiben lässt: 1445 = 275 + 845 + 1105 + 1335; Diese Identität wurde im Jahr 1966 entdeckt und widerlegte eine von Leonhard Euler im Jahr 1769 vermutete Verallgemeinerung des großen Satz von Fermat.
- 163
- Größte Zahl d, für die
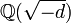 Klassenzahl 1 hat. Deshalb ist
Klassenzahl 1 hat. Deshalb ist
- Größte Zahl d, für die
-
- ungewöhnlich nahe an einer ganzen Zahl.
- 168
- Ordnung der zweitkleinsten nichtabelschen einfachen Gruppe.
- 191
- Größte rechtsstutzbare Primzahl zur Basis 4.
- 196
- Kleinster und bekanntester Kandidat für eine Lychrel-Zahl.
- 210
- Größte derzeit bekannte goldbachsche Zahl.
- 219
- Anzahl der dreidimensionalen Symmetriegruppen ohne Berücksichtigung der Orientierung im Raum (Raumgruppe).
- 220
- Kleinste befreundete Zahl, zusammen mit der 284 das kleinste befreundete Zahlenpaar.
- 223
- Die einzige natürliche Zahl, die sich nicht als Summe von weniger als 37 positiven fünften Potenzen schreiben lässt (siehe: waringsches Problem).
- 230
- Anzahl der dreidimensionalen Symmetriegruppen unter Berücksichtigung der Orientierung im Raum (Raumgruppe).
- 239
- Die größte und neben der 23 die einzige natürliche Zahl, die sich nicht als Summe von weniger als 9 Kubikzahlen schreiben lässt (siehe: waringsches Problem).
- 251
- Kleinste natürliche Zahl, die sich auf zwei verschiedene Arten als Summe von 3 Kubikzahlen schreiben lässt, nämlich als
- 13 + 53 + 53 = 23 + 33 + 63
- Kleinste natürliche Zahl, die sich auf zwei verschiedene Arten als Summe von 3 Kubikzahlen schreiben lässt, nämlich als
- 255
- Größter binärer Wert, den eine 8-Bit-Variable annehmen kann: 255 = 28 − 1 = [1111.1111]2 = [FF]16
- 256
- Anzahl binärer Werte, die eine 8-Bit-Variable annehmen kann: 256 = 28
- 257
- Fermat-Zahl F3.
- 284
- Zweitkleinste befreundete Zahl, zusammen mit der 220 das kleinste befreundete Zahlenpaar.
- 292
- Fünfte Zahl in der Kettenbruchentwicklung der Kreiszahl π. Da diese Zahl relativ groß ist, liefert der nach der vierten Stelle abgebrochene Kettenbruch
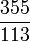 eine sehr gute Näherung für π: Die beiden Zahlen stimmen in 6 Nachkommastellen überein, das ist eine wesentlich bessere Näherung, als für einen Näherungsbruch mit einem Nenner dieser Größenordnung zu erwarten wäre.
eine sehr gute Näherung für π: Die beiden Zahlen stimmen in 6 Nachkommastellen überein, das ist eine wesentlich bessere Näherung, als für einen Näherungsbruch mit einem Nenner dieser Größenordnung zu erwarten wäre.
- Fünfte Zahl in der Kettenbruchentwicklung der Kreiszahl π. Da diese Zahl relativ groß ist, liefert der nach der vierten Stelle abgebrochene Kettenbruch
- 325
- Kleinste Zahl, die sich auf drei Weisen als Summe zweier Quadratzahlen schreiben lässt: 325 = 12 + 182 = 62 + 172 = 102 + 152
- 341
- Kleinste Pseudoprimzahl zur Basis 2
- 353
- Kleinste positive natürliche Zahl, deren Biquadrat sich als Summe von vier positiven Biquadraten schreiben lässt:
- 3534 = 304 + 1204 + 2724 + 3154
- Kleinste positive natürliche Zahl, deren Biquadrat sich als Summe von vier positiven Biquadraten schreiben lässt:
- 429
- Siebte Catalan-Zahl.
- 454
- Größte natürliche Zahl, die sich nicht als Summe von weniger als acht Kubikzahlen schreiben lässt (siehe: waringsches Problem).
- 466
- Größte natürliche Zahl, die sich nicht als Summe von weniger als 32 positiven ganzzahligen fünften Potenzen schreiben lässt. (siehe: waringsches Problem).
- 495
- Dreistellige Kaprekar-Konstante
- 496
- Dritte vollkommene Zahl
- 561
- Kleinste Carmichael-Zahl
- 563
- Dritte und derzeitig größte bekannte Wilson-Primzahl
- 858
- Zweitkleinste Giuga-Zahl mit vier Faktoren.
- 880
- Anzahl der magischen Quadrate vierter Ordnung, die nicht durch Spiegelung oder Drehung auseinander hervorgehen.
- 945
- Kleinste ungerade abundante Zahl.
Bis 10.000
- 1009
- Kleinste vierstellige Mirpzahl
- 1093
- Erste Wieferich-Primzahl
- 1105
- Kleinste Zahl, die sich auf vier Weisen als Summe zweier Quadratzahlen schreiben lässt:
- 1105 = 42 + 332 = 92 + 322 = 122 + 312 = 232 + 242
- Kleinste Zahl, die sich auf vier Weisen als Summe zweier Quadratzahlen schreiben lässt:
- 1233
- 12² + 33²
- 1722
- Dritte Giuga-Zahl.
- 1729
- Kleinste Zahl, die sich auf zwei verschiedene Weisen als Summe zweier dritter Potenzen darstellen lässt: 103 + 93 = 123 + 13 (Hardy-Ramanujan-Zahl).
- Die erste Carmichael-Zahl der Form (6n + 1)·(12n + 1)·(18n + 1).
- 1806
- Dritte primär pseudovollkommene Zahl.
- 2047
- M11 = 211 − 1: die kleinste Mersenne-Zahl mit primen Exponenten, die nicht prim, also keine Mersenne-Primzahl ist: 2047 = 23 · 89
- 2437
- Größte rechtsstutzbare Primzahl zur Basis 5.
- 2520
- Achzehnte Hochzusammengesetzte Zahl – sie hat insgesamt 48 Teiler. Außerdem ist sie die größte „besondere“ hochzusammengesetzte Zahl: Die Zahl der Teiler wird erst bei einer Verdoppelung des Zahlenwertes überboten. (5040 hat bereits 60 Teiler)
- 3511
- Zweite (und bisher größte bekannte) Wieferich-Primzahl
- 5525
- Kleinste Zahl, die sich auf sechs Weisen als Summe zweier Quadratzahlen schreiben lässt:
- 5525 = 92 + 742 = 142 + 732 = 222 + 712 = 252 + 702 = 412 + 622 = 502 + 552
- Kleinste Zahl, die sich auf sechs Weisen als Summe zweier Quadratzahlen schreiben lässt:
- 5777 und 5993
- die einzigen beiden bekannten ungeraden Zahlen, die sich nicht als
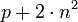 schreiben lassen, wobei p eine Primzahl und n eine ganze Zahl ist[2]
schreiben lassen, wobei p eine Primzahl und n eine ganze Zahl ist[2]
- die einzigen beiden bekannten ungeraden Zahlen, die sich nicht als
- 6174
- Kaprekar-Konstante für vierstellige Zahlen.
- 6841
- Größte rechtsstutzbare Primzahl zur Basis 7.
- 8128
- Vierte vollkommene Zahl
- 8191
- 8833
- 88² + 33²
Bis 1 Million
- 10.100
- 10² + 100² (gilt für alle Stellenwertsysteme)
- 16.843
- Erste Wolstenholme-Primzahl
- 29.341
- 10. Carmichael-Zahl, kleinste Pseudoprimzahl zu den Basen 2, 3, 5, 7 und 11.
- 41.041
- Kleinste Carmichael-Zahl mit 4 Primfaktoren
- 47.058
- Vierte primär pseudovollkommene Zahl.
- 63.973
- Carmichael-Zahl M4(1)
- 65.533
- Funktionswert a(4,1) = a(5,0) der Ackermannfunktion.
- 65.535
- Größter binärer Wert, den eine 16-Bit-Variable annehmen kann: 65.535 = 216 − 1 = [1111.1111.1111.1111]2 = [FFFF]16
- 65.536
- Anzahl binärer Werte, die eine 16-Bit-Variable annehmen kann: 65.536 = 216
- 65.537
- Fermat-Zahl F4
- 66.198
- Vierte Giuga-Zahl.
- 78.557
- Kleinste bekannte Sierpiński-Zahl.
- 108.863
- Größte rechtsstutzbare Primzahl zur Basis 6.
- 131.071
- 142.857
- Kleinste nicht-triviale Zyklische Zahl.
- 148.349
- Die einzige Zahl, die gleich der Summe ihrer der Subfakultät unterzogenen Ziffern ist.
- 177.147
- Anzahl der Möglichkeiten (311) beim Fußballtoto (Elferwette)
- 294.409
- Carmichael-Zahl M3(6)
- 509.203
- Kleinste bekannte Riesel-Zahl.
- 524.287
- 549.945
- 1. Kaprekar-Konstante für sechsstellige Zahlen.
- 617.716
- Die 1111-te Dreieckszahl, ein Palindrom; Von Charles Trigg entdeckt.
- 631.764
- 2. Kaprekar-Konstante für sechsstellige Zahlen.
- 990.100
- 990² + 100²
Bis 1 Milliarde
- 2.082.925
- Kleinste Zahl, die sich auf 18 verschiedene Weisen als Summe zweier Quadratzahlen schreiben lässt:
- 2.082.925 = 262 + 14432 = 1342 + 14372 = 1632 + 14342 = 1952 + 14302 = 3302 + 14052 = 3702 + 13952 = 4292 + 13782 = 5312 + 13422 = 5412 + 13382 = 5582 + 13312 = 5792 + 13222 = 7022 + 12612 = 7302 + 12452 = 7552 + 12302 = 8452 + 11702 = 8942 + 11332 = 9262 + 11072 = 10142 + 10272
- Kleinste Zahl, die sich auf 18 verschiedene Weisen als Summe zweier Quadratzahlen schreiben lässt:
- 2.124.679
- Zweite Wolstenholme-Primzahl
- 4.005.625
- Kleinste Zahl, die sich auf 20 Weisen als Summe zweier Quadratzahlen schreiben lässt
- 4.497.359
- Größte rechtsstutzbare Primzahl zur Basis 8.
- 5.882.353
- 5882 + 23532
- 5.928.325
- Kleinste Zahl, die sich auf 24 Weisen als Summe zweier Quadratzahlen schreiben lässt
- 9.721.368
- Größte Zahl aus verschiedenen Ziffern (im Dezimalsystem), aus der man eine beliebige Ziffer streichen kann, so dass der Rest durch die gestrichene Ziffer teilbar ist
- 33.550.336
- Fünfte vollkommene Zahl
- 56.052.361
- Carmichael-Zahl M3(35)
- 73.939.133
- Größte Primzahl, für die gilt, dass bei Wegstreichen der letzten Ziffer wieder eine Primzahl mit genau dieser Eigenschaft entsteht; d. h., 7393913, 739391, 73939, 7393, 739, 73, 7 sind auch Primzahlen.
- 94.122.353
- 94122 + 23532
- 118.901.521
- Carmichael-Zahl M3(45)
- 146.511.208
- 19 + 49 + 69 + 59 + 19 + 19 + 29 + 09 + 89
- 172.947.529
- Carmichael-Zahl M3(51)
- 216.821.881
- Carmichael-Zahl M3(55)
- 228.842.209
- Carmichael-Zahl M3(56)
- 275.305.224
- Anzahl der magischen Quadrate fünften Ordnung, die nicht durch Spiegelung oder Drehung auseinander hervorgehen.
- 472.335.975
- 49 + 79 + 29 + 39 + 39 + 59 + 99 + 79 + 59
- 534.494.836
- 59 + 39 + 49 + 49 + 99 + 49 + 89 + 39 + 69
- 635.318.657
- Kleinste Zahl, die sich auf zwei verschiedene Arten als Summe von zwei Biquadraten schreiben lässt, nämlich als
- 1584 + 594 = 1334 + 1344.
- Kleinste Zahl, die sich auf zwei verschiedene Arten als Summe von zwei Biquadraten schreiben lässt, nämlich als
- 912.985.153
- 99 + 19 + 29 + 99 + 89 + 59 + 19 + 59 + 39
Bis 1 Billion
- 1.299.963.601
- Carmichael-Zahl M3(100)
- 1.355.840.309
- Größte rechtsstutzbare Primzahl zur Basis 9.
- 1.765.038.125
- 17650² + 38125²
- 2.147.483.647
- 2.214.408.306
- Fünfte Giuga-Zahl.
- 2.214.502.422
- Fünfte primär pseudovollkommene Zahl.
- 2.301.745.249
- Carmichael-Zahl M3(121)
- 2.584.043.776
- 25840² + 43776²
- 4.294.967.295
- Größter binärer Wert, den eine 32-Bit-Variable annehmen kann:
- 4.294.967.295 = 232 − 1 = [1111.1111.1111.1111.1111.1111.1111.1111]2 = [FFFF.FFFF]16
- Größter binärer Wert, den eine 32-Bit-Variable annehmen kann:
- 4.294.967.296
- Anzahl binärer Werte, die eine 32-Bit-Variable annehmen kann: 4.294.967.296 = 232
- 4.294.967.297
- Anhand dieser Zahl widerlegte Euler eine Vermutung von Fermat – siehe fermatsche Primzahl.
- 4.679.307.774
- 410 + 610 + 710 + 910 + 310 + 010 + 710 + 710 + 710 + 410
- 5.391.411.025
- Kleinste abundante Zahl, die weder durch 2 noch durch 3 teilbar ist.
- 6.172.882.716
- Die 111.111-te Dreieckszahl, ein Palindrom. Von Charles Trigg entdeckt.
- 7.416.043.776
- 74160² + 43776²
- 8.235.038.125
- 82350² + 38125²
- 8.589.869.056
- Sechste vollkommene Zahl, 1588 von Cataldi entdeckt.
- 15.170.835.645
- Kleinste Zahl, die sich auf drei verschiedene Arten als Summe von je zwei Kubikzahlen schreiben lässt, nämlich als
- 5173 + 24683 = 7093 + 24563 = 17333 + 21523
- Kleinste Zahl, die sich auf drei verschiedene Arten als Summe von je zwei Kubikzahlen schreiben lässt, nämlich als
- 24.423.128.562
- Sechste Giuga-Zahl.
- 32.164.049.650
- 311 + 211 + 111 + 611 + 411 + 011 + 411 + 911 + 611 + 511 + 011
- 52.495.396.602
- Sechste primär pseudovollkommene Zahl.
- 116.788.321.168
- 116788² + 321168²
- 123.288.328.768
- 123288² + 328768²
- 137.438.691.328
- Siebte vollkommene Zahl, 1588 von Cataldi entdeckt.
- 192.739.365.541
- Carmichael-Zahl M4(45)
- 200.560.490.131
- Ist die Primzahl 31# + 1, wobei 31# das Produkt aller Primzahlen von 2 bis 31 ist (siehe auch Satz von Euklid, Primfakultät).
- 461.574.735.553
- Carmichael-Zahl M4(56)
- 876.712.328.768
- 876712² + 328768²
- 883.212.321.168
- 883212² + 321168²
Bis 1 Trillion
- 10.028.704.049.893
- Carmichael-Zahl M4(121)
- 28.116.440.335.967
- 214 + 814 + 114 + 114 + 614 + 414 + 414 + 014 + 314 + 314 + 514 + 914 + 614 + 714
- 61.728.399.382.716
- Die 11.111.111te Dreieckszahl, ein Palindrom.
- 432.749.205.173.838
- Die siebte Giuga-Zahl
- 4.338.281.769.391.370
- 416 + 316 + 316 + 816 + 216 + 816 + 116 + 716 + 616 + 916 + 316 + 916 + 116 + 316 + 716 + 016
- 9.585.921.133.193.329
- Die kleinste Carmichael-Zahl nach dem System von Richard G. E. Pinch
- 14.737.133.470.010.574
- Die achte Giuga-Zahl
- 21.897.142.587.612.075
- 217 + 117 + 817 + 917 + 717 + 117 + 417 + 217 + 517 + 817 + 717 + 617 + 117 + 217 + 017 + 717 + 517
- 48.988.659.276.962.496
- Die kleinste Zahl, die sich auf fünf verschiedene Arten als Summe von je zwei Kubikzahlen schreiben lässt, nämlich als
- 231.5183 + 331.9543 = 221.4243 + 336.5883 = 205.2923 + 342.9523 = 107.8393 + 362.7533 = 38.7873 + 365.7573
- Die kleinste Zahl, die sich auf fünf verschiedene Arten als Summe von je zwei Kubikzahlen schreiben lässt, nämlich als
- 550.843.391.309.130.318
- Die neunte Giuga-Zahl
Über 1 Trillion
- 1.517.841.543.307.505.039
- 119 + 519 + 119 + 719 + 819 + 419 + 119 + 519 + 419 + 319 + 319 + 019 + 719 + 519 + 019 + 519 + 019 + 319 + 919
- 2.305.843.008.139.952.128
- Die achte vollkommene Zahl, 1750 von Leonhard Euler entdeckt.
- 2.305.843.009.213.693.951
- Mersenne-Primzahl M61
- 12.157.692.622.039.623.539
- 11 + 22 + 13 + 54 + 75 + 66 + 97 + 28 + 69 + 210 + 211 + 012 + 313 + 914 + 615 + 216 + 317 + 518 + 319 + 920
- 18.446.744.073.709.551.615
- Größter binärer Wert, den eine 64-Bit-Variable annehmen kann: 18.446.744.073.709.551.615 = 264 − 1 = [1111.1111.1111.1111.1111.1111.1111.1111.1111.1111.1111.1111.1111.1111.1111.1111]2 = [FFFF.FFFF.FFFF.FFFF]16
- 18.446.744.073.709.551.616
- Anzahl binärer Werte, die eine 64-Bit-Variable annehmen kann: 18.446.744.073.709.551.616 = 264
- 63.105.425.988.599.693.916
- 620 + 320 + 120 + 020 + 520 + 420 + 220 + 520 + 920 + 820 + 820 + 520 + 920 + 920 + 620 + 920 + 320 + 920 + 120 + 620
- 128.468.643.043.731.391.252
- 121 + 221 + 821 + 421 + 621 + 821 + 621 + 421 + 321 + 021 + 421 + 321 + 721 + 321 + 121 + 321 + 921 + 121 + 221 + 521 + 221
- 357.686.312.646.216.567.629.137
- Größte Primzahl im Dezimalsystem, die von rechts beginnend ausschließlich aus Primzahlen besteht. D. h., nimmt man vorn (links) einen beliebigen Teil der Zahl weg, so bleibt stets eine Primzahl übrig.
- 244.197.000.982.499.715.087.866.346
- Die zehnte bekannte Giuga-Zahl
- 618.970.019.642.690.137.449.562.111
- Mersenne-Primzahl M89
- 554.079.914.617.070.801.288.578.559.178
- Die elfte bekannte Giuga-Zahl.
- 8.490.421.583.559.688.410.706.771.261.086
- Die siebente primär pseudovollkommene Zahl.
- 162.259.276.829.213.363.391.578.010.288.127
- Mersenne-Primzahl M107
- 1.910.667.181.420.507.984.555.759.916.338.506
- Die zwölfte bekannte Giuga-Zahl.
- 2.658.455.991.569.831.744.654.692.615.953.842.176
- Die neunte vollkommene Zahl, 1883 von Pervusin entdeckt.
- 170.141.183.460.469.231.731.687.303.715.884.105.727
- Mersenne-Primzahl M127
- 191.561.942.608.236.107.294.793.378.084.303.638.130.997.321.548.169.216
- Die zehnte vollkommene Zahl, 1911 von Powers entdeckt.
- 808.017.424.794.512.875.886.459.904.961.710.757.005.754.368.000.000.000
- Die Ordnung der Monstergruppe (der größten sporadischen Gruppe).
- 13.164.036.458.569.648.337.239.753.460.458.722.910.223.472.318.386.943.117.783.728.128
- Die elfte vollkommene Zahl, 1914 von Powers entdeckt.
- 6.086.555.670.238.378.989.670.371.734.243.169.622.657.830.773.351.885.970.528.324.860.512.791.691.264
- Die zweite erhabene Zahl, von Kevin Brown entdeckt
- 14.474.011.154.664.524.427.946.373.126.085.988.481.573.677.491.474.835.889.066.354.349.131.199.152.128
- Die zwölfte vollkommene Zahl, 1876 von Lucas entdeckt.
- 2520 (2521 − 1)
- Die 13. vollkommene Zahl, 1952 von Robinson entdeckt.
- 2606 (2607 − 1)
- Die 14. vollkommene Zahl, 1952 von Robinson entdeckt.
- 21278 (21279 − 1)
- Die 15. vollkommene Zahl, 1952 von Robinson entdeckt.
- 22202 (22203 − 1)
- Die 16. vollkommene Zahl, 1952 von Robinson entdeckt.
- 22280 (22281 − 1)
- Die 17. vollkommene Zahl, 1952 von Robinson entdeckt.
- 1,29*10865
- Die untere Schranke für die maximale Anzahl von Einsen eines haltenden Busy Beaver mit 6 Zuständen
- 23216 (23217 − 1)
- Die 18. vollkommene Zahl, 1957 von Riesel entdeckt.
- 3*101730
- Die untere Schranke für die maximale Anzahl von Schritten eines haltenden Busy Beaver mit 6 Zuständen
- 24252 (24253 − 1)
- Die 19. vollkommene Zahl, 1961 von Adolf Hurwitz und Selfridge entdeckt.
- 24422 (24423 − 1)
- Die 20. vollkommene Zahl, 1961 von Adolf Hurwitz und Selfridge entdeckt.
- 29688 (29689 − 1)
- Die 21. vollkommene Zahl, 1963 von Gillies entdeckt.
- 29940; (29941 − 1)
- Die 22. vollkommene Zahl, 1963 von Gillies entdeckt.
- 211.212 (211.213 − 1)
- Die 23. vollkommene Zahl, 1963 von Gillies entdeckt.
- 219.936 (219.937 − 1)
- Die 24. vollkommene Zahl, 1971 von Tuckerman entdeckt.
- 221.700 (221.701 − 1)
- Die 25. vollkommene Zahl, 1978 von Noll und Nickel entdeckt.
- 223.208 (223.209 − 1)
- Die 26. vollkommene Zahl, 1979 von Noll entdeckt.
- 265.536 − 3
- Funktionswert a(4,2) der Ackermannfunktion (Dezimalzahl mit 19.729 Ziffern)
- 244.496 (244.497 − 1)
- Die 27. vollkommene Zahl, 1979 von Slowinski und Nelson entdeckt.
- 286.242 (286.243 − 1)
- Die 28. vollkommene Zahl, 1982 von Slowinski entdeckt.
- 48.047.305.725 × 2172.403 − 1
- Bis 2008 größte bekannte Sophie-Germain-Primzahl.
- 2110.502 (2110.503 − 1)
- Die 29. vollkommene Zahl, 1988 von Colquit und Welsh entdeckt.
- 2132.048 (2132.049 − 1)
- Die 30. vollkommene Zahl, 1983 von Slowinski entdeckt.
- 2216.090 (2216.091 − 1)
- Die 31. vollkommene Zahl, 1985 von Slowinski entdeckt.
- 481.899 × 2481.899 + 1
- Bis 2008 größte bekannte Cullen-Primzahl C481.899
- 1.354.828 × 21.354.828 + 1
- Die größte bekannte Cullen-Primzahl C1.354.828
- 2756.838 (2756.839 − 1)
- Die 32. vollkommene Zahl, 1992 von Slowinski und Gage entdeckt.
- 2859.432 (2859.433 − 1)
- Die 33. vollkommene Zahl, 1993 von Slowinski.
- 3.752.948 × 23.752.948 − 1
- Die größte bekannte Woodall-Primzahl C'3.752.948
- 225.964.951 − 1
- Die 42. bekannte Mersenne-Primzahl, eine Zahl mit 7.816.230 Ziffern
- 230.402.457 − 1
- Die 43. bekannte Mersenne-Primzahl, eine Zahl mit 9.152.052 Ziffern
- 232.582.657 − 1
- Die 44. bekannte Mersenne-Primzahl, eine Zahl mit 9.808.358 Ziffern
- 243.112.609 − 1
- Die 46. bekannte Mersenne-Primzahl und damit die größte bekannte Primzahl (Stand September 2008), eine Zahl mit 12.978.189 Ziffern
- 70388830…50240001
- Mit 16.142.049 Stellen die (bis 1996) größte gefundene Carmichael-Zahl, die 1.101.518 verschiedene Primteiler besitzt. Gefunden wurde sie von Löh und Niebuhr.
- 232.582.656 (232.582.657 − 1)
- Die größte bekannte vollkommene Zahl
- 22.305.843.009.213.693.951 − 1
- Diese doppelte Mersennezahl, die man auch als
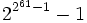 schreiben kann und etwa 790 Billiarden Ziffern hat, ist möglicherweise eine Primzahl. Dies zu widerlegen, ist erklärte Aufgabe des GIMPS-Projektes, das verteilte Rechenleistung über das Internet koordiniert.
schreiben kann und etwa 790 Billiarden Ziffern hat, ist möglicherweise eine Primzahl. Dies zu widerlegen, ist erklärte Aufgabe des GIMPS-Projektes, das verteilte Rechenleistung über das Internet koordiniert.
- Diese doppelte Mersennezahl, die man auch als
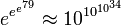
- Skewes-Zahl, lange Zeit (1931–1971) die größte in einem mathematischen Beweis verwendete endliche Zahl. (siehe MathWorld)
- Mega
- Megistron
- Mosers Zahl
- Grahams Zahl (G64)
- Verdrängte Skewes' Zahl von Platz 1.
Unendliche Größen
- ∞
- Unendlich, in bestimmten Rechensystemen der Kehrwert von 0, ist größer als alle Zahlen dieser Liste und ist selbst keine Zahl. Mit ∞ lässt sich zwar in beschränktem Umfang rechnen, jedoch sind viele Ausdrücke, die ∞ enthalten, entweder selbst ∞ oder nicht definiert.
 (aleph 0), ω (klein Omega)
(aleph 0), ω (klein Omega)
 ist die abzählbare Mächtigkeit der natürlichen, rationalen und algebraischen Zahlen und damit die kleinste transfinite Kardinalzahl. ω ist die kleinste Ordinalzahl, die größer ist als jede natürliche Zahl, und damit die kleinste transfinite Ordinalzahl. Es gilt zwar ω =
ist die abzählbare Mächtigkeit der natürlichen, rationalen und algebraischen Zahlen und damit die kleinste transfinite Kardinalzahl. ω ist die kleinste Ordinalzahl, die größer ist als jede natürliche Zahl, und damit die kleinste transfinite Ordinalzahl. Es gilt zwar ω =  , die Arithmetik mit diesen Zahlen unterscheidet sich jedoch.
, die Arithmetik mit diesen Zahlen unterscheidet sich jedoch.
- ε0
- Die kleinste Ordinalzahl, die nicht mit einer endlichen Anzahl von Rechenoperationen (Addition, Multiplikation, Potenzierung) von ω aus erreichbar ist. Sie ist immer noch abzählbar, deshalb gilt ω =
 < ε0 <
< ε0 < 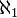 = ω1
= ω1
- Die kleinste Ordinalzahl, die nicht mit einer endlichen Anzahl von Rechenoperationen (Addition, Multiplikation, Potenzierung) von ω aus erreichbar ist. Sie ist immer noch abzählbar, deshalb gilt ω =
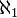
- Die nach
 nächstgrößere Mächtigkeit. Sofern man die Kontinuumshypothese akzeptiert, stimmt sie mit der Mächtigkeit c des Kontinuums (der Menge der reellen Zahlen) überein.
nächstgrößere Mächtigkeit. Sofern man die Kontinuumshypothese akzeptiert, stimmt sie mit der Mächtigkeit c des Kontinuums (der Menge der reellen Zahlen) überein.
- Die nach
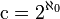
- Die überabzählbare Mächtigkeit der irrationalen, transzendenten, reellen und komplexen Zahlen und Quaternionen, die Mächtigkeit der Potenzmenge der natürlichen Zahlen.
Komplexe Zahlen
In dieser Teilliste sind besondere komplexe Zahlen versammelt und nach ihrem Betrag geordnet.
- i
- Die imaginäre Einheit. Eine komplexe Zahl, deren Quadrat den Wert −1 hat und die damit Lösung der quadratischen Gleichung x2 + 1 = 0 ist. i ist vierte Einheitswurzel. Siehe auch imaginäre Zahlen.
- -i
- Kehrwert der imaginären Einheit i
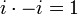 oder
oder 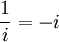 (inverses Element der Multiplikation, hier aber auch der Addition:
(inverses Element der Multiplikation, hier aber auch der Addition: 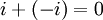 ). −i ist wie i vierte Einheitswurzel.
). −i ist wie i vierte Einheitswurzel.
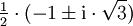
- Die primitiven dritten Einheitswurzeln; die dritte Potenz dieser beiden Zahlen ist 1.
- πi
- Liefert als Argument der Exponentialfunktion den Wert −1, siehe eulersche Identität.
- 2πi
- Periode der komplexen Exponentialfunktion.
- 1/2 + i·14,134725141734693…
- Nullstelle der riemannschen Zetafunktion mit dem kleinsten, positiven imaginären Anteil.
Zahlen mit besonderer Bedeutung
Bis 0
- 0
- Der Eispunkt bezeichnet den Gefrierpunkt von Wasser unter Normalbedingungen in Grad Celsius. Siehe auch 0
- Als Absoluter Nullpunkt stellt 0 Kelvin die tiefst mögliche Temperatur dar.
Bis 1
- 0,5
- Als Bruch ½ (ein Halbes) der einzige echte Bruch, der in den meisten Sprachen seit jeher eine spezielle Bezeichnung hat.
- 1
- Numerischer Wert der milesisch-griechischen Zahl Alpha.
Bis 10
- 1,0594630943592952… (Folge A010774 in OEIS)
![\sqrt[12]{2}](/pictures/dewiki/55/70b8b8fc763c20423a65bd934e378085.png) , Frequenzverhältnis eines Halbtons bei gleichstufiger Stimmung
, Frequenzverhältnis eines Halbtons bei gleichstufiger Stimmung
- 1,4142135623730950… (Folge A002193 in OEIS)
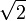 , Seitenverhältnis vieler Papierformate, zum Beispiel DIN-A- und DIN-B-Formate mit dem Seitenverhältnis
, Seitenverhältnis vieler Papierformate, zum Beispiel DIN-A- und DIN-B-Formate mit dem Seitenverhältnis 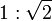
- 1,5
- Mit der speziellen Bezeichnung „anderthalb“ traditionell sprachlich besonders hervorgehobene gebrochene Zahl. Auch andere Sprachen (z. B. das Russische) kennen eine spezielle Bezeichnung dieser Zahl.
- 2
- Mann und Frau.
- Symbol für Gegensätze.
- In der chinesischen Philosophie Yin und Yang.
- Numerischer Wert der milesisch-griechischen Zahl Beta.
- 3
- Dimension des Raums, in dem wir leben.
- Zahl der Wiederholungen zur Affirmation (Bekräftigung) in Mythologie und Spiritualität.
- Anzahl aller guten Dinge.
- Sooft leugnete Petrus, bevor ein Hahn krähte (Passion).
- Dreifaltigkeit Vater, Sohn, Hl. Geist.
- Anzahl der klassischen Aggregatzustände.
- Anzahl der Grund- bzw. Primärfarben.
- Drittes Geschlecht für Menschen, die von heteronormativen Regeln abweichen.
- Numerischer Wert der milesisch-griechischen Zahl Gamma.
- 4
- Anzahl der Elemente in der Antike.
- Vier Himmelsrichtungen. Vier Jahreszeiten.
- Vier kanonische Evangelien und Evangelisten.
- Chinesische und japanische Unglückszahl (wird wie „Tod“ ausgesprochen).
- In der westlichen Welt steht sie für Glück (Kleeblatt).
- Numerischer Wert der milesisch-griechischen Zahl Delta.
- 5
- Anzahl der Elemente in Asien.
- Basis-Zahl im Alten Ägypten im Sinne von 5=4+1 (Pyramide) und in Vielfachen von 5, vermutlich symbolisch für den menschlichen Körper: 5 (4+1) Gliedmaßen, Finger, Zehen.
- Pyramide mit 5 Seiten und 5 Ecken kleinster Körper, der immer auf seine Grundseite fällt.
- Dem Pentagramm (fünfeckigen Stern) wird magische Besonderheit zugeschrieben.
- Numerischer Wert der milesisch-griechischen Zahl Epsilon.
- 6
- Anzahl der Quarks (up, down, charm, strange, top und bottom).
- Der Hexaeder (Würfel) ist einer der platonischen Körper.
- Der Davidstern ist der sechseckige Stern.
- Numerischer Wert der milesisch-griechischen Zahl Stigma.
- 7
- Anzahl der Tage einer Woche.
- Häufig auch in Märchen benutzt:
- Der Wolf und die sieben jungen Geißlein
- Schneewittchen und die sieben Zwerge
- Das tapfere Schneiderlein erlegte sieben (Fliegen) auf einen Streich
- Numerischer Wert der milesisch-griechischen Zahl Zeta.
- Anzahl der Kristallsysteme des dreidimensionalen Gitters.
- Im Christentum symbolisiert die 7 (übernatürliche) Vollständigkeit.
- Anzahl der Tage des Schöpfungszyklus
- Je sieben Paare von reinen Tieren sollte Noach mit in die Arche nehmen.
- In der Offenbarung: sieben Gemeinden, Siegel, Posaunen, Engel, Plagen, Schalen, siebenköpfiges Tier.
- Im Katholizismus sieben Todsünden.
- Anzahl der mit bloßem Auge sichtbaren, von der Erde als Zentralpunkt aus beweglich erscheinenden Himmelskörper (Sonne, Mond, Merkur, Venus, Mars, Jupiter, Saturn)[3]
- 8
- Glückszahl in China
- Heilige Zahl in Indien
- Numerischer Wert der milesisch-griechischen Zahl Eta.
- In unserem Sonnensystem umkreisen acht Planeten[4] die Sonne.
- 9
- Numerischer Wert der milesisch-griechischen Zahl Theta.
- heilige Zahl der Baha'i.
- Zahl des Selbst im Satanismus.
- 10
- Die Zehn Gebote
- Anzahl der Finger sowie der Zehen
- Die 10 steht symbolisch für die irdische Vollkommenkeit
- Numerischer Wert der milesisch-griechischen Zahl Iota.
- Im Christentum und Judentum symbolisiert die 10 Vollständigkeit (aber der 7 unterlegen).
Bis 100
- 11
- Kleinste Schnapszahl
- Närrische Zahl im Rheinischen Karneval:
- Beginn des Karnevals am 11.11. um 11 Uhr 11
- Der Elferrat ist das Parlament des Narrenreiches in Karneval, Fastnacht und Fasching
- Die „Fußball-Elf“: je Team sind elf Spieler auf dem Feld
- Früher auch als „dreckiges Dutzend“ bezeichnet
- 12
- Anzahl der Pentominos
- Ein Dutzend
- Die Basis frühgeschichtlicher Zahlsysteme
- Ein Symbol der Vollkommenheit
- In der Bibel …
- die 12 Stämme Israels und oft in Bezugnahmen auf diese
- die 12 Apostel Jesu
- 12 ist die Anzahl der Stunden, die sich die Sonne am Tag zeigt, und die Anzahl der Monate des Jahres
- In der Musik besteht eine Oktave aus 12 Halbtönen
- Es gibt 12 Tierkreiszeichen
- 12 Olympische Götter
- 12 Aufgaben gab König Eurystheus dem Herakles („Dodekathlos“)
- 12 bewohnte Inseln der Dodekanes
- 12 Sterne auf der Europaflagge
- 13
- Unglückszahl und/oder Glückszahl
- Die Wilde Dreizehn
- 14
- Anzahl der Stationen eines Kreuzwegs
- Chinesische Unglückszahl (wird wie „Der sichere Tod“ (ohne Entkommen) ausgesprochen)
- Kindergebet „14 Englein um mich stehen“.
- 16
- Mit sechzehn Jahren erreicht man in vielen Gesellschaften eine Vorstufe des Erwachsenendaseins, etwa das Schutzalter in der Schweiz oder die Fahrerlaubnis in den USA
- 17
- Unglückszahl in Italien
- 18
- Der 18. Geburtstag ist in den meisten Staaten der Tag der Volljährigkeit
- Bei den Juden, bei denen Zahlen durch Buchstaben ausgedrückt werden, bedeutet der Zahlenwert 18 Leben
- Die Israeliten hatten 18 Minuten Zeit, um aus Ägypten auszuziehen
- Die Matzen zum Passach-Fest dürfen nicht länger als 18 Minuten gefertigt werden
- Unter Neonazis ist die 18 Codezahl für „Adolf Hitler“, nach dem ersten und achten Buchstaben des Alphabets
- 20
- Numerischer Wert der milesisch-griechischen Zahl Kappa
- 21
- Punktzahl, die beim Glücksspiel Black Jack bzw. 17 und 4 angestrebt wird
- Früher das Alter der Volljährigkeit
- 22
- Anzahl der Buchstaben des hebräischen Alphabets
- 23
- Spielt eine Rolle in diversen Verschwörungstheorien, u. a. als angebliche Zahl der Illuminaten
- Kleinste Zahl von Personen mit zufälligen Geburtstagen, für die es wahrscheinlicher ist, dass zwei am selben Tag Geburtstag haben, als dass alle an verschiedenen Tagen Geburtstag haben (Geburtstagsproblem)
- 24
- Anzahl der Stunden eines Tages
- Anzahl der Bücher des Tanach
- Anzahl der Buchstaben im griechischen Alphabet
- 25
- Jubiläumszahl; häufig auch als „Silbernes Jubiläum“ bezeichnet, z. B. „Silberne Hochzeit“ am 25. Hochzeitstag
- 26
- Anzahl der Buchstaben im lateinischen Alphabet
- 27
- Anzahl der Bücher des Neuen Testaments in den deutschen Bibelausgaben
- 27,322:
- Die Anzahl der Tage, die der Mond für einen Umlauf um die Erde benötigt (siderischer Monat)
- 28
- Unter Rechtsradikalen Codezahl für „Blood & Honour“
- 4 Wochen haben 28 Tage
- Anzahl der Tage des Monats Februar im „normalen“ Kalenderjahr
- 29
- Anzahl der Tage des Monats Februar im Schaltjahr
- 29,530588…
- Tage, Synodische Periode des Mondes (danach wiederholen sich die Mondphasen)
- 30
- Numerischer Wert der milesisch-griechischen Zahl Lambda
- 32
- 37
- Anzahl der Zahlen, auf die man beim französischen Roulette setzen kann
- 39
- Anzahl der Bücher des Alten Testaments in den deutschen evangelischen Bibelausgaben
- 40
- Steht als Symbol für Prüfung, Bewährung, Initiation, Tod
- In der Bibel …
- dauerte die Sintflut 40 Tage
- war Moses 40 Tage und 40 Nächte bei Gott, um das Gesetz zu empfangen
- dauerte der israelitische Auszug aus Ägypten 40 Jahre
- war Isaak 40 Jahre, als er Rebekka zu Frau nahm
- war Esau 40 Jahre, als er Judith zur Frau nahm
- war Josua 40, als er von Mose ausgesandt wurde das Land „Kadesch-Barnea“ auszukundschaften
- wurde Jesus 40 Tage vom Teufel versucht
- war Isch-Boschet 40, als er König über Israel wurde
- regierte König David 40 Jahre über Israel, König Joas regierte ebenfalls 40 Jahre
- Die Pest-Quarantäne dauerte 40 Tage
- Anzahl der Karten …
- beim Doppelkopf (Version „ohne Luschen“)
- bei einem ecuatorianischen Kartenspiel („Cuarenta“ = dt. „Vierzig“)
- Numerischer Wert der milesisch-griechischen Zahl My
- 42
- Im Roman Per Anhalter durch die Galaxis kommt die Zahl 42 als Antwort auf die Frage nach „dem Leben, dem Universum und dem ganzen Rest“ vor
- 43
- Ordnungszahl des ersten chemischen Elements ohne stabile Isotope (Technetium)
- 46
- Typische Anzahl der menschlichen Chromosomen
- 50
- Jubiläumszahl; häufig auch als „Goldenes Jubiläum“ bezeichnet, z. B. „Goldene Hochzeit“ am 50. Hochzeitstag
- Pfingsten ist am fünfzigsten Tag nach Ostern (Ostern mitgezählt)
- Numerischer Wert der milesisch-griechischen Zahl Ny
- 52
- Heilige Zahl der Mayas, nach 52 Jahren beginnt der Kalender neu
- Anzahl der Karten …
- beim Spiel Bridge (Kartenspiel)
- beim Spiel Rommé
- beim Spiel Canasta
- Anzahl der Wochen eines Jahres
- 60
- Ein Schock, fünf Dutzend
- Höchste mit einem Einzelwurf beim Dart-Spiel erzielbare Punktzahl
- Anzahl Kohlenstoffatome im einfachsten Fulleren C60
- Numerischer Wert der milesisch-griechischen Zahl Xi
- 62
- Zahl der Monate in einer Yuga-Periode
- 64
- Anzahl der Hexagramme im Yijing
- Anzahl der Felder eines Schachbretts
- 66
- Anzahl der Bücher der Bibel
- Im englischsprachigen Raum werden die einleitenden Anführungszeichen (“) aufgrund ihrer Form manchmal scherzhaft 66 genannt – analog dazu 99 für die schließenden Anführungszeichen (”)
- 69
- Eine sexuelle Stellung, bei der sich beide Partner gleichzeitig gegenseitig oral befriedigen
- 70
- Numerischer Wert der milesisch-griechischen Zahl Omikron
- 72
- 75
- „Kronjuwelenhochzeit“, höchste Bezeichnung für die Dauer von Jahren nach einer Eheschließung
- 80
- Numerischer Wert der milesisch-griechischen Zahl Pi
- 81
- Tetragramme im I-Ging = Anzahl der Verse von Laotses „Tao te king“
- Kürzel für die Hells Angels
- 82
- 88
- Sprichwörtlich: „Egal wie ~“
- Szenekürzel für „HH“ / Heil Hitler unter Neonazis, da H der 8. Buchstabe des Alphabets ist
- Funkersprache: „Liebe und Küsse“
- In China Kürzel für „Bye-Bye“ wegen der Aussprache der Zahlen
- 90
- Rechter Winkel, gemessen in Grad
- Numerischer Wert der milesisch-griechischen Zahl Qoppa
- 97
- Oft gewählt als Beispiel für eine beliebige Zahl; viele Bibliotheken stempeln Seite 97
- 99
- Letzte ganze Zahl vor der Hundert, wird im Sinne von eins vor der Vollständigkeit gerne als literarisches Element verwendet zum Beispiel bei Nenas 99 Luftballons, dem Lied 99 bottles of beer und 99 Namen Allahs
- Zahl der Monate in einer Oktaeteris-Periode
- 100
- Rechter Winkel, gemessen in Gon
- Siedepunkt von Wasser in Grad Celsius unter Normalbedingungen
- Numerischer Wert der milesisch-griechischen Zahl Rho
Bis 1000
- 101
- Raum 101 kommt in mehreren Romanen und Filmen vor, so beispielsweise in dem Roman 1984 von George Orwell, Matrix, A Beautiful Mind, Kill Bill – Volume 2 etc.[5]
- 108
- Heilige Zahl im Hinduismus und Buddhismus
- 114
- 122
- Jeanne Calment, höchstes Alter, das ein Mensch bislang (2005) nachweislich erreichte
- 128
- Anzahl der Zeichen in einem 7-Bit-Code (ASCII)
- 137,035 999 76(50)
- Kehrwert der Feinstrukturkonstante
- 144
- 1 Gros
- 12 Dutzend
- 144 Ellen beträgt die Höhe der Mauer des Neuen Jerusalem in Offb. 21,17
- Rettungsnotrufnummer in Österreich und der Schweiz
- 147
- Maximum Break, jedoch nicht höchstmögliches Break beim Snooker
- 150
- Anzahl der Psalmen
- 153
- Steht in der christlichen Zahlensymbolik für die gesamte Menschheit
- 156
- Produkt aus einem Dutzend (12) und einem „Dutzend des Teufels“ (13)
- 168
- Anzahl der Stunden einer Kalenderwoche
- 170
- Höchstmögliches Finish beim Dart im „Double-Out“-Modus
- 187
- Steht für Mord oder Morddrohung; stammt von der US-amerikanischen Polizei, die unter dem Kürzel '187' Mordfälle codiert
- 200
- Numerischer Wert der milesisch-griechischen Zahl Sigma
- 212
- Siedepunkt von Wasser in Grad Fahrenheit unter Normalbedingungen
- 235
- Zahl der Monate im Metonschen Kalender-Zyklus
- 256
- Anzahl der mit einem Byte darstellbaren Zeichen
- 260
- Zahl der Tage in einem Tonalamatl
- 300
- Numerischer Wert der milesisch-griechischen Zahl Tau
- 313
- Auto-Kennzeichen von Donald Duck, steht für 13. März oder 3 mal 13
- 354
- Zahl der Tage in einem Mondjahr (6 × 29 + 6 × 30)
- 360
- Anzahl der Tage eines Jahres bei der Zinsrechnung (in Deutschland)
- Zahlenwert des Vollwinkels in Grad
- Anzahl der Monate im islamischen Kalender-Zyklus
- 365
- Anzahl der Tage im Kalenderjahr
- 365,24219…
- Dauer des tropischen Jahres (das die Jahreszeiten bestimmt) in Tagen
- 366
- Anzahl der Tage im Schaltjahr
- 400
- Zahlenwert des Vollwinkels in Gon
- Nach 400 Jahren wiederholt sich der bürgerliche gregorianische Kalender (also ohne Osterdatum, aber das gleiche Kalenderdatum fällt danach stets wieder auf den gleichen Wochentag)
- Numerischer Wert der milesisch-griechischen Zahl Ypsilon
- 419
- Steht für Vorschussbetrug, nach dem Paragrafen 419 des nigerianischen Strafgesetzbuchs
- 500
- Größter Wert einer Euro-Banknote
- Numerischer Wert der milesisch-griechischen Zahl Phi
- 532
- Nach 532 Jahren wiederholt sich der julianische Kalender
- 555
- Siehe 555 (Telefonnummer)
- 600
- Numerischer Wert der milesisch-griechischen Zahl Chi
- 613
- 616
- In einigen alten Bibelhandschriften statt der 666 in Offb. 13,18
- 666
- Biblisch die „Zahl des Tieres“ bzw. Antichristen (Offb. 13,18)
- Zahl der Satanisten und des Teufels
- 700
- Numerischer Wert der milesisch-griechischen Zahl Psi
- 777
- Mystisch/biblisch die „göttliche Zahl“; mit der Bedeutung der absoluten Perfektion
- 800
- Numerischer Wert der milesisch-griechischen Zahl Omega
- 888
- „Christus-Zahl“
- 911
- Notrufnummer in Nordamerika
- 911 steht auch für den Terrorakt des 11. September 2001 (9/11)
- 940
- Zahl der Monate in einem kallippischen Zyklus
- 969
- Alter des Methusalem, des ältesten in der Bibel erwähnten Menschen 1. Buch Mose (Genesis, 5,21-27)
- 1000
- Größte römische Ziffer (M)
- In der Bibel im Kapitel 20 der Offenbarung Tausendjähriges Reich Christi; auch in nationalsozialistischer Rhetorik
Bis 10.000
- 1001
- Arabische magische Zahl (zum Beispiel „Märchen aus 1001 Nacht“)
- 1024
- Basis für die IEC-Binärpräfixe. 1 KiB = 210 Byte = 10241 Byte
- 1089
- Man bildet zu einer dreistelligen Zahl, die nicht aus drei gleichen Ziffern besteht, ihre Umkehrzahl, z. B. ist 327 die Umkehrzahl von 723, und subtrahiert die kleinere von der größeren Zahl; zu dem Ergebnis addiert man dann die Umkehrzahl des Ergebnisses (wenn das erste Zwischenergebnis lediglich zweistellig ist, stellt man der Zahl eine Null voran); bei diesem Verfahren erhält man stets das Ergebnis 1089
- 1189
- Anzahl der Kapitel der Bibel
- 1337
- 1435
- Normalspurweite der Eisenbahn in Millimetern
- 1440
- Anzahl der Minuten eines Tages
- Anzahl Kilobyte einer normalformatierten 3,5″-Diskette
- 2701
- Wichtige Zahl im Cryptonomicon
- 4711
- Wird als metasyntaktische Variable für endlich große Kardinalzahlen verwendet; der Hintergrund ist, dass diese Zahl gerade keine besonderen mathematischen Eigenschaften aufweist, sondern ein bekannter Markenname für Kölnisch Wasser ist
- 6666
- 7200
- Zahl der Tage in einer Katun-Periode
- 8766
- Anzahl der Stunden eines Jahres nach dem Julianischen Kalender
- 10.000
- Eine Myriade
- In China wünscht man sich soviele Jahre Glück
Bis 1 Million
- 10.631
- Zahl der Tage in einer islamischen Periode
- 12.000
- 18.980
- Ist 52×365 – soviel Tage beträgt die Kalender-Periode der Mayas
- 27.759
- Zahl der Tage im kallippischen Zyklus
- 31.169
- Anzahl der Verse der Bibel
- 44.760
- Anzahl der Krieger von Ruben (1 Chr 5,18)
- 86.400
- Anzahl von Sekunden in einem Tag
- 144.000
- Mystisch/biblische Zahl der Geretteten am Tag des jüngsten Gerichts; abgeleitet von „12×12×1000 Menschen“ bzw. je 12.000 Söhne aus den 12 Stämmen Israels (Offb 7,4)
- 146.097
- Zahl der Tage im 400-jährigen gregorianischen Kalender-Zyklus
- 304.805
- Anzahl der Buchstaben in der Tora
Bis 1 Milliarde
- 1.048.576
- 1 MiB = 220 Byte = 10242 Byte
- 3.674.160
- Anzahl der Positionen eines Rubik-Würfels der Größe 2 × 2 × 2 (Pocket Cube), die durch manuelles Verdrehen erreicht werden können
- 3.447.360
- Zahl der Jahre im jüdischen Kalender-Zyklus
- 5.700.000
- Zahl der Jahre im gregorianischen Oster-Zyklus (danach ist stets wieder zum selben Datum Ostern)
- 8.145.060
- Anzahl der Möglichkeiten beim Schweizer und Österreichischem Zahlenlotto „6 aus 45“; die Wahrscheinlichkeit für einen „Sechser“ beträgt 1 zu 8.145.060
- 10.518.300
- Anzahl der möglichen Kombinationen für die Kartenhand eines Spielers beim Schafkopf
- 13.983.816
- Anzahl der möglichen Kombinationen im deutschen Lotto „6 aus 49“
- 16.777.216
- 224; Verwendung in der EDV, z. B. die Anzahl der möglichen Farbabstufungen bei 24 Bit Farbtiefe
- 76.275.360
- Anzahl der Möglichkeiten beim Euro-Millions Lotto: 5 aus 50 Zahlen und 2 aus 9 Sternen
- 299.792.458
- Die Lichtgeschwindigkeit im Vakuum, definiert in m/s
Über 1 Milliarde
- 1.073.741.824
- 1 GiB = 230 Byte = 10243 Byte.
- 1.099.511.627.776
- 1 TiB = 240 Byte = 10244 Byte.
- 1.000.000.000.000.000
- Eine Billiarde = 1015.
- 99.561.092.450.391.000
- Anzahl möglicher Kartenverteilungen beim Schafkopf.
- 18.446.744.073.709.551.615 (264 − 1)
- Anzahl der Weizenkörner, die Sissa ibn Dahir nach der Weizenkornlegende vom indischen Herrscher Shihram für die Erfindung des Schachspiels erhalten sollte.
- 43.252.003.274.489.856.000
- Anzahl der Positionen eines Rubik-Würfels der Größe 3×3×3, die durch manuelles Verdrehen erreicht werden können.
- 6.670.903.752.021.072.936.960
- Anzahl möglicher Sudoku-Rätsel (9×9).
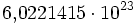
- Avogadro-Konstante, Anzahl der Moleküle in einer Stoffmenge von 1 Mol.
- 7.401.196.841.564.901.869.874.093.974.498.574.336.000.000.000 (rund
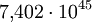 )
) - Anzahl der Positionen eines Rubik-Würfels der Größe 4×4×4 (Master Cube), die durch manuelles Verdrehen erreicht werden können.
- 81.171.437.193.104.932.746.936.103.027.318.645.818.654.720.000 (rund
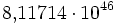 )
) - Anzahl möglicher Sudoku-Rätsel (12×12).
- 282.870.942.277.741.856.536.180.333.107.150.328.293.127.731.985.672.134.721.536.000.000.000.000.000 (rund
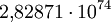 )
) - Anzahl der Positionen eines Rubik-Würfels der Größe 5×5×5 (Professor’s Cube), die durch manuelles Verdrehen erreicht werden können.
- 10100
- Ein Googol
- 19.500.551.183.731.307.835.329.126.754.019.748.794.904.992.692.043.434.567.152.132.912.323.232.706.135.469.180.065.278.712.755.853.360.682.328.551.719.137.311.299.993.600.000.000.000.000.000.000.000.000.000.000.000 (rund
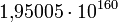 )
) - Anzahl der Positionen eines V-Cube 7 (Zauberwürfel der Größe 7x7x7), die durch manuelles Verdrehen erreicht werden können.
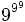 (ist definiert als
(ist definiert als 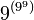 )
)- größte Zahl, die man im Dezimalsystem mit nicht mehr als drei Ziffern und ohne weitere Symbole darstellen kann.
- 10Googol =
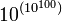
- Ein Googolplex
- 10(Googolplex)
- Ein Googolplexplex, auch Googolplexian genannt
- 10Googolplexplex =
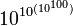 Googolplexplexplex
Googolplexplexplex - 10Googolplexplexplex =
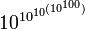 Googolplexplexplexplex
Googolplexplexplexplex
Literatur
- F. Le Lionnais: Les Nombres Remarquables. Hermann, Paris 1983
- David Wells: Das Lexikon der Zahlen. Fischer, Frankfurt am Main 1991, ISBN 3596101352
Siehe auch
Weblinks
Einzelnachweise
- ↑ Folge A004023 in OEIS
- ↑ http://www.spiegel.de/wissenschaft/mensch/0,1518,598096,00.html
- ↑ Unter günstigen Sichtbedingungen ist auch Uranus mit bloßem Auge sichtbar.
- ↑ Von seiner Entdeckung im Jahr 1930 bis zur Neudefinition des Begriffs Planet im Jahr 2006 galt Pluto als neunter Planet in unserem Sonnensystem.
- ↑ „Room 101“ in der englischsprachigen Wikipedia
- ↑ tatsächlich sind es weniger, siehe dazu http://www.diyanet.gov.tr/german/sorular.asp?id=26
Wikimedia Foundation.

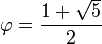
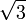 , die
, die