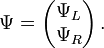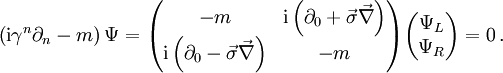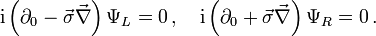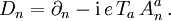Bi-Spinor

Die Weyl-Gleichung, nach Hermann Weyl benannt, ist die Diracgleichung für masselose Teilchen mit Spin-1/2. Sie wird bei der Beschreibung der schwachen Wechselwirkung verwendet.

Die Darstellung der Lorentzgruppe auf Dirac-Spinoren ist reduzibel. In einer geeigneten Darstellung der Dirac-Matrizen, in der Weyl-Darstellung, transformieren die ersten beiden und die letzten beiden Komponenten der 4er-Spinoren getrennt,

$\Psi= \begin{pmatrix} \Psi_L\\ \Psi_R \end{pmatrix}\,.$

Die 2er-Spinoren Ψ_L und Ψ_R sind die links- und rechtshändigen Weyl-Spinoren.

Sie werden in der Diracgleichung für ein freies Spin-1/2-Teilchen durch die Masse m gekoppelt,

$\left(\mathrm i\gamma^n \part_n-m\right)\Psi= \begin{pmatrix} -m& \mathrm i\left(\part_0+\vec{\sigma}\vec{\nabla}\right)\\ \mathrm i\left(\part_0-\vec{\sigma}\vec{\nabla}\right)&-m \end{pmatrix} \begin{pmatrix} \Psi_L\\ \Psi_R \end{pmatrix} =0\,.$

Hierbei sind σ₁,σ₂,σ₃ die Pauli-Matrizen.

Verschwindet die Masse, 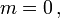$m=0\,,$ so zerfällt die Diracgleichung in je eine Weyl-Gleichung für den links- und den rechtshändigen Spinor

$\mathrm i\left(\part_0-\vec{\sigma}\vec{\nabla}\right)\Psi_L=0\,,\quad \mathrm i\left(\part_0+\vec{\sigma}\vec{\nabla}\right)\Psi_R=0\,.$

Zur Beschreibung der schwachen Wechselwirkung ist wichtig, dass die links- und rechthändigen Spinoren unterschiedlich, aber lorentzinvariant, an Vektorfelder koppeln können. Die Kopplung entsteht durch Ersetzung der Ableitungen durch sogenannte kovariante Ableitungen

$D_n = \partial_n - \mathrm i\,e\,T_a\,A^a_n\,.$

Dabei bezeichnet 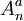$A^a_n$ die Komponenten der Vektorfelder und T_a Matrizen (die die Lie-Algebra der Eichgruppe darstellen). Die Zahl e ist die Kopplungskonstante. Die Darstellungsmatrizen können bei den linkshändigen und rechthändigen Spinoren verschieden sein. Bei der schwachen Wechselwirkung verschwinden bei den rechtshändigen Spinoren die Matrizen, 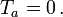$T_a=0\,.$ Die rechtshändigen Spinoren haben keine schwache Wechselwirkung. Da die Kopplung von linkshändigen und rechthändigen Spinoren verschieden ist, spricht man auch von chiraler Kopplung.