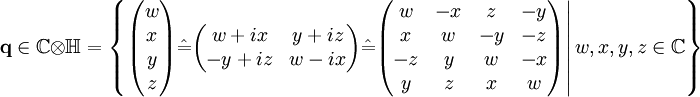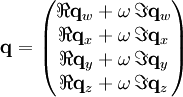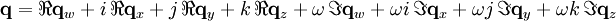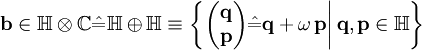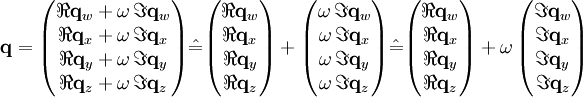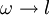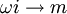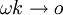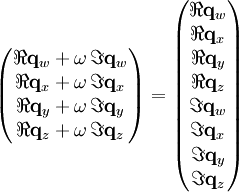Biquaternionen

Die Biquaternionen sind ein hyperkomplexes Zahlensystem, das von William Kingdon Clifford in der zweiten Hälfte des 19. Jahrhunderts beschrieben wurde. Vor Clifford hatte Arthur Cayley bereits die Quaternionen mit komplexen Koeffizienten (also die Menge 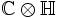$\mathbb{C}\otimes\mathbb{H}$) als Biquaternionen bezeichnet.

Hamilton Biquaternion

Die von Arthur Cayley beschriebenen Biquaternionen sind Quaternionen, deren Elemente komplexe Zahlen sind. Dies kann – durch die Umwandlung des Quaternions – dargestellt werden, wobei das Quaternion als 4-Vektor, als komplexe 2×2-Matrix oder als 4×4-Matrix dargestellt wird:

$\mathbf{q} \in \mathbb{C}\otimes\mathbb{H} = \left\{ \left. \begin{pmatrix} w \\ x \\ y \\ z \end{pmatrix} \hat{=} \begin{pmatrix} w+ix & y+iz \\ -y+iz & w-ix \end{pmatrix} \hat{=} \begin{pmatrix} w & -x & z & -y \\ x & w & -y & -z \\ -z & y & w & -x \\ y & z & x & w \end{pmatrix} \right\vert w,x,y,z \in \Bbb{C} \right\}$

Die Biquaternionen sind also ein 8-dimensionales hyperkomplexes Zahlensystem mit den Einheiten 1, i, j, k, ω, ωi, ωj, ωk. Ein Biquaternion q kann also z. B. wie folgt dargestellt werden:

$\mathbf{q} = \begin{pmatrix} \Re\mathbf{q}_w + \omega\,\Im\mathbf{q}_w \\ \Re\mathbf{q}_x + \omega\,\Im\mathbf{q}_x \\ \Re\mathbf{q}_y + \omega\,\Im\mathbf{q}_y \\ \Re\mathbf{q}_z + \omega\,\Im\mathbf{q}_z \end{pmatrix}$

$\mathbf{q} = \Re\mathbf{q}_w + i\,\Re\mathbf{q}_x + j\,\Re\mathbf{q}_y + k\,\Re\mathbf{q}_z + \omega\,\Im\mathbf{q}_w + \omega i\,\Im\mathbf{q}_x + \omega j\,\Im\mathbf{q}_y + \omega k\,\Im\mathbf{q}_z$

Hierbei sind i, j und k die Einheiten der Quaternionen. Es gilt zudem ω² = 1, und dass ω mit i, j und k kommutiert. Die Komponenten w, x, y und z stellen die jeweiligen Dimensionen dar, die durch das Quaternion repräsentiert werden. Die Verbindung entsteht durch 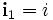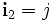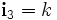$\mathbf{i}_1 =i$, $\mathbf{i}_2 =j$, $\mathbf{i}_3 =k$ und $\mathbf{i}_1\mathbf{i}_2\mathbf{i}_3 =\omega$.

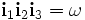Clifford Biquaternion

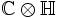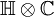Die Clifford-Biquaternionen entstehen durch die Idee, die komplexen Zahlen in den Hamilton-Biquaternionen durch eine geteilte komplexe Zahl zu ersetzen. Dies erreicht man durch Umformung des Ausdrucks $\mathbb{C}\otimes\mathbb{H}$ in $\mathbb{H}\otimes\mathbb{C}$. Dies kann man sich so vorstellen, dass man anstatt einem „Quaternion mit komplexen Zahlen“ eine „komplexe Zahl mit Quaternionen“ bildet. Alternativ kann man sich die Biquaternionen als direkte Summe der Quaternionen mit sich selbst, also 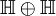$\mathbb{H} \oplus \mathbb{H}$, bilden. Für das Biquaternion b kann dies so definiert werden:

$\mathbf{b} \in \mathbb{H}\otimes\mathbb{C} \hat{=} \mathbb{H} \oplus \mathbb{H} \equiv \left\{ \left. \begin{pmatrix} \mathbf{q} \\ \mathbf{p} \end{pmatrix} \hat{=} \mathbf{q} + \omega\,\mathbf{p} \right\vert \mathbf{q},\mathbf{p} \in \Bbb{H} \right\}$

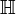Hierbei ist $\mathbb{C}$ die Menge der komplexen Zahlen, $\mathbb{H}$ die Menge der Quaternionen; q und p sind Quaternionen und ω² = 1.

Umformung

Die Clifford-Biquaternionen entsprechen der Clifford-Algebra 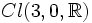$Cl(3,0,\mathbb R)$ und bilden einen assoziativen Ring mit Nullteilern.

Die Hamilton-Biquaternionen und die Clifford-Biquaternionen sind Darstellungsformen der Biquaternionen. Ein Hamilton-Biquaternion entspricht dabei einem Clifford-Biquaternion:

$\mathbf{q} = \begin{pmatrix} \Re\mathbf{q}_w + \omega\,\Im\mathbf{q}_w \\ \Re\mathbf{q}_x + \omega\,\Im\mathbf{q}_x \\ \Re\mathbf{q}_y + \omega\,\Im\mathbf{q}_y \\ \Re\mathbf{q}_z + \omega\,\Im\mathbf{q}_z \end{pmatrix} \hat{=} \begin{pmatrix} \Re\mathbf{q}_w \\ \Re\mathbf{q}_x \\ \Re\mathbf{q}_y \\ \Re\mathbf{q}_z \end{pmatrix} + \begin{pmatrix} \omega\,\Im\mathbf{q}_w \\ \omega\,\Im\mathbf{q}_x \\ \omega\,\Im \mathbf{q}_y \\ \omega\,\Im\mathbf{q}_z \end{pmatrix} \hat{=} \begin{pmatrix} \Re\mathbf{q}_w \\ \Re\mathbf{q}_x \\ \Re\mathbf{q}_y \\ \Re\mathbf{q}_z \end{pmatrix} + \omega\,\begin{pmatrix}\Im\mathbf{q}_w \\ \Im\mathbf{q}_x \\ \Im \mathbf{q}_y \\ \Im\mathbf{q}_z \end{pmatrix}$

Zudem können Biquaternionen über die folgenden Rechenregeln in Oktonionen umgewandelt werden:

$\omega \to l$

$\omega i \to m$

$\omega j \to n$

$\omega k \to o$

Dadurch gilt:

$\begin{pmatrix} \Re\mathbf{q}_w + \omega\,\Im\mathbf{q}_w \\ \Re\mathbf{q}_x + \omega\,\Im\mathbf{q}_x \\ \Re\mathbf{q}_y + \omega\,\Im\mathbf{q}_y \\ \Re\mathbf{q}_z + \omega\,\Im\mathbf{q}_z \end{pmatrix} = \begin{pmatrix} \Re\mathbf{q}_w \\ \Re\mathbf{q}_x \\ \Re\mathbf{q}_y \\ \Re\mathbf{q}_z \\ \Im\mathbf{q}_w \\ \Im\mathbf{q}_x \\ \Im\mathbf{q}_y \\ \Im\mathbf{q}_z \end{pmatrix}$

Anwendung

Biquaternionen werden ua. benötigt um 8-dimensionale Räume beschreiben zu können. Hierbei werden die Zeit und die Raumdimensionen als komplexe Zahlen dargestellt, um die Zeitdilatation und Raumkrümmung abzubilden.

Ein einfacherer Anwendungsfall ist die Verwendung des Biquaternions zur Darstellung einer Geraden (Vertex) im 4-dimensionalen Raum (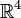$\mathbb{R}^4$), wobei der Realteil den Stützvektor und der Imaginärteil den Richtungsvektor repräsentiert. Zur Verwendung in der animierten 3D-Computergrafik wird hierbei für den Faktor 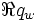$\Re q_w$ die Zeit t eingesetzt — der Faktor 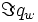$\Im q_w$ wird nicht benötigt und daher gleich null gesetzt.

Referenzen

• W. K. Clifford; Preliminary Sketch of Biquaternions.; Proc. London Math. Soc. 4, 381-395, 1873
• W. R. Hamilton; [http://www.amazon.com/exec/obidos/ASIN/B0006P67CY/ref=nosim/weisstein-20 Lectures on Quaternions: Containing a Systematic Statement of a New Mathematical Method; Hodges and Smith, Dublin, 1853
• E. Study, Von den Bewegung und Umlegungen]; Math. Ann. 39, 441-566, 1891.
• van der Waerden, B. L. A History of Algebra from al-Khwarizmi to Emmy Noether; Springer-Verlag, Seiten 188-189, New York, 1985

Siehe auch

• Zahlenbereiche
  • Ganze Zahl
  • Rationale Zahl
  • Reelle Zahl
  • Komplexe Zahl
• Hyperkomplexe Zahlen:
  • Oktave (Oktonion)
  • Quaternion
  • Sedenion