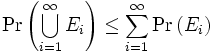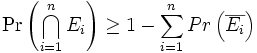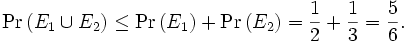Bonferroniungleichungen

Die Bonferroni-Ungleichungen sind Formeln, die zur Abschätzung der Wahrscheinlichkeit des Durchschnitts bzw. der Vereinigung von Ereignissen dienen.

Benennung nach Bonferroni

Die Bonferroni-Ungleichungen werden nicht unbedingt zurecht nach Carlo Emilio Bonferroni benannt.

Bonferroni war eigentlich nicht der Urheber dieser Ungleichungen, er benutzt sie aber, um einen statistischen Schätzer zu definieren (Bonferroni-Methode). Die Benennung nach ihm ist daher vor allem in statistischen Kreisen beliebt. Aufgrund ihrer Einfachheit sind die Ungleichungen jedoch sicher schon vor ihm bekannt gewesen.

Die erste der folgende Ungleichungen wird häufiger nach George Boole als Boolesche Ungleichung bezeichnet; oft werden diese Ungleichung aber auch einfach ohne Namensbezug genannt.

Erste Ungleichung

Im Folgenden seien E_i beliebige Teilmengen (Ereignisse) in einem Wahrscheinlichkeitsraum Ω. Dann gilt:

$\Pr\left( \bigcup_{i=1}^nE_i \right) \leq \sum_{i=1}^n \Pr\left(E_i\right)$.

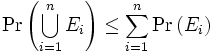Es gilt auch allgemeiner:

$\Pr\left( \bigcup_{i=1}^\infty E_i \right) \leq \sum_{i=1}^\infty \Pr\left(E_i\right)$

Diese Ungleichungen werden auch Boolesche Ungleichungen genannt.

Beweis

Zum Beweis der ersten Variante genügt eine vollständige Induktion nach n. Der Induktionsanfang ergibt sich unmittelbar aus

$\Pr \left( E_1 \cup E_2 \right) = \frac{|E_1 \cup E_2|}{|\Omega|} = \frac{|E_1| + |E_2| - |E_1 \cap E_2|}{|\Omega|}$

$\leq \frac{|E_1| + |E_2|}{|\Omega|} = \frac{|E_1|}{|\Omega|} + \frac{|E_2|}{|\Omega|} = \Pr \left( E_1 \right) + \Pr \left( E_2 \right)$.

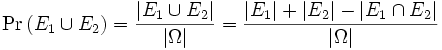
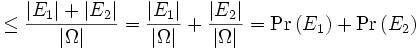Sei für den Induktionsschritt 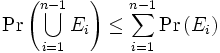$\Pr\left( \bigcup_{i=1}^{n-1}E_i \right) \leq \sum_{i=1}^{n-1} \Pr\left(E_i\right)$ vorausgesetzt. Es folgt dann die Behauptung vermöge: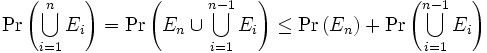

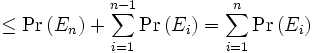$\Pr\left( \bigcup_{i=1}^{n}E_i \right) = \Pr\left( E_n \cup \bigcup_{i=1}^{n-1}E_i \right) \leq \Pr\left( E_n \right) + \Pr \left( \bigcup_{i=1}^{n-1}E_i \right)$

$\leq \Pr\left( E_n \right) + \sum_{i=1}^{n-1} \Pr\left(E_i\right) = \sum_{i=1}^{n} \Pr\left(E_i\right)$.

Zweite Ungleichung

Im Folgenden seien wieder E_i beliebige Teilmengen (Ereignisse) in einem Wahrscheinlichkeitsraum Ω. Ferner bezeichne 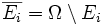$\overline{E_i} = \Omega \setminus E_i$ das Komplement von E_i. Dann folgt:

$\Pr\left(\bigcap_{i=1}^nE_i\right) \geq 1-\sum_{i=1}^nPr\left(\overline{E_i}\right)$

Beweis

Zunächst beobachtet man, dass stets 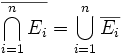$\overline{\bigcap_{i=1}^nE_i} = \bigcup_{i=1}^{n}\overline{E_i}$ gilt. Der Beweis ergibt sich dann sofort, indem man in die erste Ungleichung 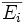$\overline{E_i}$ statt E_i einsetzt und die komplementäre Wahrscheinlichkeit bildet.

Beispiele

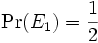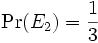• Sei Ω = {1,2,3,4,5,6} die Menge der Ergebnisse eines Würfelwurfs. Bezeichne E₁ = {2,4,6} das Ereignis, eine gerade Zahl zu würfen und E₂ = {5,6} das Ereignis, wenigstens eine 5 zu würfen. Offensichtlich gilt $\Pr(E_1) = \frac{1}{2}$ und $\Pr(E_2) = \frac{1}{3}$. Nach der ersten Bonferroni-Ungleichung gilt für das Ereignis, eine gerade Zahl oder wenigstens eine 5 zu würfeln

$\Pr \left( E_1 \cup E_2 \right) \leq \Pr \left( E_1 \right) + \Pr \left( E_2 \right) = \frac{1}{2} + \frac{1}{3} = \frac{5}{6} .$

• Sei das Szenario wie im vorausgehenden Beispiel. Nach der zweiten Bonferroni-Ungleichung gilt für das Ereignis, eine gerade Zahl und mindestens eine 5 zu würfeln

$\Pr \left( E_1 \cap E_2 \right) \geq 1 - \Pr \left( \overline{E_1} \right) - \Pr \left( \overline{E_2} \right) = 1 - (1-\frac{1}{2}) - (1-\frac{1}{3}) = - \frac{1}{6}$

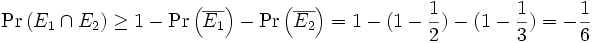
Das Ergebnis liefert also keine brauchbare Aussage, da jede Wahrscheinlichkeit ohnehin größer oder gleich Null ist. Für das Ereignis, eine gerade Zahl und weniger als eine 5 zu würfeln folgt jedoch

$\Pr \left( E_1 \cap \overline{E_2} \right) \geq 1 - \Pr \left( \overline{E_1} \right) - \Pr \left( E_2 \right) = 1 - (1-\frac{1}{2}) - (1-\frac{2}{3}) = \frac{1}{6} .$

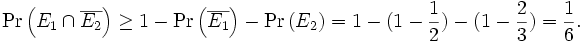
Literatur

• Janos Galambos, Italo Simonelli: Bonferroni-type Inequalities with Applications, Springer-Verlag, 1996.
• Klaus Dohmen: Improved Bonferroni Inequalities via Abstract Tubes - Inequalities and Identities of Inclusion-Exclusion Type, Springer-Verlag, 2003.
• Ulrich Krengel: Einführung in die Wahrscheinlichkeitstheorie und Statistik, 7. Auflage, Vieweg Verlag, 2003.