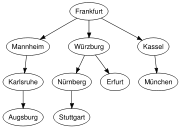
Breitendurchlauf

Breitensuche

Breitensuche (Breadth First Search) ist ein Fachbegriff der Informatik, welcher ein Verfahren zum Durchsuchen bzw. Durchlaufen der Knoten eines Graphens bezeichnet. Sie zählt zu den uninformierten Suchen.

Arbeitsweise

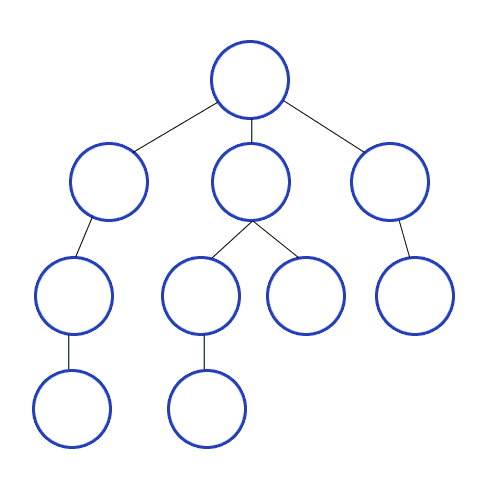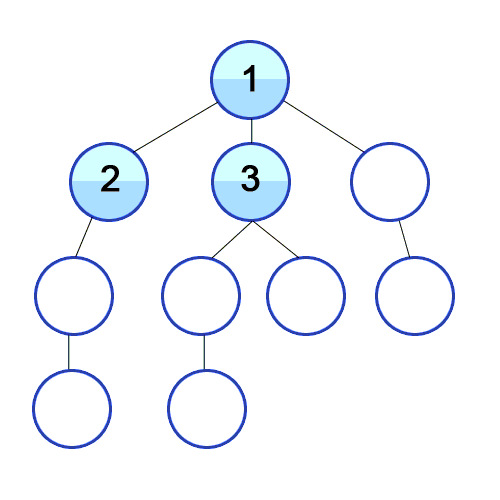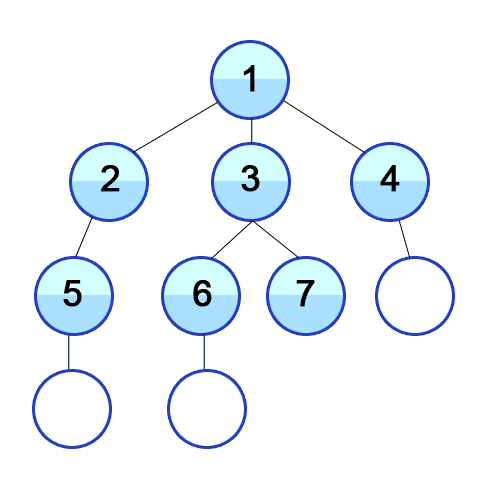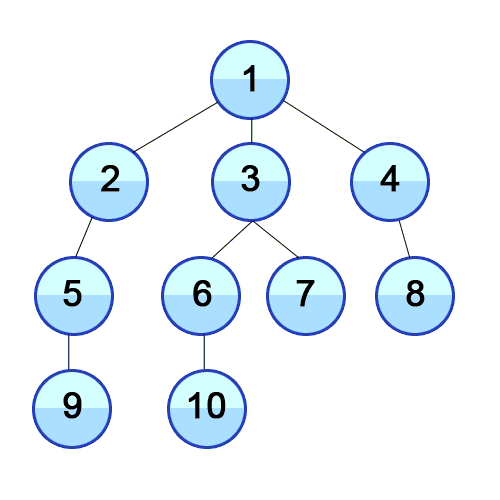
Die Breitensuche ist eine uninformierte Suche, welche durch Expansion der einzelnen Level der Graphen ausgehend vom Startknoten den Graph in die Breite nach einem Element durchsucht.

Zuerst wird ein Startknoten u ausgewählt. Von diesem Knoten aus wird nun jede Kante (u,v) betrachtet und getestet, ob der gegenüberliegende Knoten v schon entdeckt wurde bzw. das gesuchte Element ist. Ist dies noch nicht der Fall, so wird der entsprechende Knoten in einer Warteschlange gespeichert und im nächsten Schritt bearbeitet. Hierbei ist zu beachten, dass Breitensuche immer zuerst alle direkt nachfolgenden Knoten bearbeitet, und nicht wie die Tiefensuche einem Pfad in die Tiefe folgt. Nachdem alle Kanten des Ausgangsknotens betrachtet wurden, wird der erste Knoten der Warteschlange entnommen und das Verfahren wiederholt.

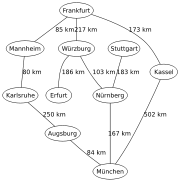Eine Landkarte von Deutschland mit den Verbindungen zwischen einigen Städten. Der Baum, welcher entsteht, wenn man BFS auf die Landkarte anwendet und in Frankfurt startet.

Algorithmus (informell)

1. Bestimme den Knoten, an dem die Suche beginnen soll, und speichere ihn in einer Warteschlange ab.
2. Entnimm einen Knoten vom Beginn der Warteschlange und markiere ihn.
   • Falls das gesuchte Element gefunden wurde, brich die Suche ab und liefere "gefunden" zurück.
   • Anderenfalls hänge alle bisher unmarkierten Nachfolger dieses Knotens, die sich noch nicht in der Warteschlange befinden, ans Ende der Warteschlange an.
3. Wiederhole Schritt 2.
4. Wenn die Warteschlange leer ist, dann wurde jeder Knoten bereits untersucht. Beende die Suche und liefere "nicht gefunden" zurück.

Eigenschaften

Bezeichne 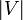$\vert V \vert$ die Anzahl der Knoten (Vertex) und 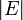$\vert E \vert$ die Anzahl der Kanten (Edge) im Graphen.

Speicherplatzverbrauch

Da alle bisher entdeckten Knoten gespeichert werden, beträgt der Speicherplatzverbrauch von Breitensuche 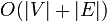$O(\vert V \vert + \vert E \vert)$. Somit ist die Breitensuche aufgrund des immensen Platzverbrauches für größere Probleme ungeeignet.
Ein der Breitensuche ähnliches Verfahren, jedoch mit deutlich geringerem Speicherplatzverbrauch, ist die iterative Tiefensuche.

Laufzeit

Da im schlimmsten Fall alle möglichen Pfade zu allen möglichen Knoten betrachtet werden müssen, beträgt die Laufzeit von Breitensuche $O(\vert V \vert + \vert E \vert)$.

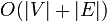Vollständigkeit

Wenn in jedem Knoten nur endlich viele Alternativen existieren, ist die Breitensuche vollständig. Dies bedeutet, dass, wenn eine Lösung existiert, diese auch gefunden wird. Dies ist unabhängig davon, ob der zugrundeliegende Graph endlich ist oder nicht. Sollte jedoch keine Lösung existieren, so divergiert die Breitensuche bei einem unendlichen Graphen.

Optimalität

Breitensuche ist im allgemeinen nicht optimal, da immer das Ergebnis mit dem kürzesten Pfad zum Anfangsknoten gefunden wird. Führt man Kantengewichte ein, so muss das Ergebnis, welches am nächsten zum Startknoten liegt, nicht notwendigerweise auch das Ergebnis mit den geringsten Pfadkosten sein. Dieses Problem umgeht man, indem man die Breitensuche zur uniformen Kostensuche erweitert. Sind jedoch alle Kantengewichte äquivalent, so ist die Breitensuche optimal, da in diesem Fall die Lösung, die am nächsten zum Ausgangsknoten liegt, auch die Lösung mit den geringsten Kosten ist.

Die uniforme Kostensuche (Uniform Cost Search) ist eine Erweiterung der Breitensuche für Graphen mit gewichteten Kanten. Der Algorithmus besucht Knoten in Reihenfolge aufsteigender Pfadkosten vom Wurzelknoten (und wird deshalb üblicherweise mit einer Priority Queue implementiert, in der alle noch nicht besuchten Nachbarn bereits besuchter Knoten mit der Pfadlänge als Schlüssel verwaltet werden). Die Optimalität ist nur für nicht-negative Kantengewichte garantiert.

Anwendung

Die Breitensuche kann für viele Fragestellungen in der Graphentheorie verwendet werden. Einige sind:

• Finde alle Zusammenhangskomponenten in einem Graph
• Finde alle Knoten innerhalb einer Zusammenhangskomponente
• Finde zwischen zwei Knoten u und w einen kürzesten Pfad (ungewichtete Kanten)
• Kürzeste-Kreise-Problem

Siehe auch

• Beschränkte Tiefensuche
• Iterative Tiefensuche
• Tiefensuche

Literatur

• Thomas H. Cormen, Charles Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. MIT Press, 2^nd edition 2001, ISBN 0262531968

Weblinks

• Bebilderte Schritt-für-Schritt-Analyse zur Breitensuche und Java-Applet

	Dieser Artikel ist als Audiodatei verfügbar:
	Speichern |
	Mehr Informationen zur „Gesprochenen Wikipedia“