%

Einheit
Norm	Hilfsmaßeinheit
Einheitenname	Prozent
Einheitenzeichen	%
Beschriebene Größe(n)	Verhältnis
Größensymbol(e)	p
Dimensionsname	1 (dimensionslos)
In SI-Einheiten	-
Benannt nach	lat. per centum (vom Hundert)
Siehe auch: Promille ppm ppb

Zahlenangaben in Prozent (lat.-it. vom Hundert, Hundertstel)^[1] dienen der Veranschaulichung und dem Vergleichbarmachen von Größenverhältnissen, indem die Größen zu einem einheitlichen Grundwert (Hundert) ins Verhältnis gesetzt werden. Daher wird das Prozent auch als Hilfsmaßeinheit für Verhältnisgrößen verwendet. Prozentangaben werden durch das Symbol % kenntlich gemacht (z. B. 63,7 %), wobei immer ein Leerzeichen zwischen die Zahl und das Prozentzeichen zu setzen ist.^[2] Der Duden empfiehlt, einen kleineren, festen Zwischenraum zu setzen.^[3]

Ältere Gesetzestexte verwenden üblicherweise die Ausdrücke „vom Hundert“ (abgekürzt: vH oder v. H.). Das DIN empfiehlt jedoch, diese Ausdrücke zu vermeiden.^[4]

Definition und Begriffe

Ein Prozent ist ein Hundertstel: 1 % = 0,01;

100 Prozent sind ein Ganzes: 100 % = 1.

Prozentangaben beschreiben Größenverhältnisse und beziehen sich immer auf einen Grundwert. Der Grundwert ist die Ausgangsgröße, auf die sich die Prozentangabe bezieht. Der Prozentsatz wird in Prozent ausgedrückt und bezeichnet ein Größenverhältnis relativ zum Grundwert. Die absolute Bestimmung dieser Größe nennt man Prozentwert. Der Prozentwert hat dieselbe Einheit wie der Grundwert. Zum Beispiel:

• „49 % (= Prozentsatz) der 15.000 Einwohner (= Grundwert) sind weiblich, das sind 7.350 Einwohner (= Prozentwert)“

Verständnis

Prozentangaben drücken Mengenverhältnisse aus und erfüllen dabei die gleiche Funktion wie die Formulierungen „ein Halb“ oder „ein Viertel“. Dabei bedeutet „ein Halb“ das gleiche wie „50 Prozent“ und „ein Viertel“ das gleiche wie „25 Prozent“. Prozentangaben können darüber hinaus auch feinere Mengenverhältnisse ausdrücken, z. B. „23 Prozent“, was 23 Hundertstel des Grundwertes entspricht.

Genau wie „ein Halb“ oder „ein Viertel“ drückt eine Prozentangabe ein Verhältnis zu einem Grundwert aus: ein Halb von welchem Grundwert? 50 Prozent von welchem Grundwert?

Die Bedeutung der Ausdrücke „um“ und „auf“ ist dabei zu unterscheiden:

• „Mein Gehalt ist um 5 Prozent gestiegen“ bedeutet das gleiche wie „Mein Gehalt ist auf 105 Prozent gestiegen“.
• „Die Miete ist um 3 Prozent gesunken“ bedeutet das gleiche wie „Die Miete ist auf 97 Prozent gesunken“.
• zum Vergleich: „Der Verbrauch ist um ein Viertel gesunken“ bedeutet das gleiche wie „Der Verbrauch ist auf drei Viertel des vorherigen Verbrauches gesunken“.

Vergleicht man Prozentwerte, kann man dies in Prozentpunkten ausdrücken:

• „Der Anteil der Miete an meinen Ausgaben ist dieses Jahr um 5 Prozentpunkte gestiegen.“

Dies kann bedeuten, dass der Anteil an den Ausgaben von 20 Prozent auf 25 Prozent gestiegen ist, aber auch von 30 Prozent auf 35 Prozent usw.

Umrechnung zwischen Zahl und Prozentsatz

Prozentsatz in Zahl umrechnen

Das Prozent-Symbol % durch seine Entsprechung „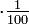$\cdot \tfrac{1}{100}$“ ersetzen. Beispiel:

50 % ist das gleiche wie 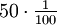$50 \cdot \tfrac{1}{100}$, also 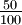$\tfrac{50}{100}$ oder als gekürzter Bruch $\tfrac{1}{2}$.

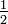Zahl in Prozentsatz umrechnen

Den Bruch mit 100 % (was das Gleiche wie 1 ist) multiplizieren. Beispiel:

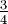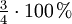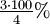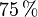$\tfrac{3}{4}$ ist das gleiche wie $\tfrac{3}{4} \cdot 100\,%$, also $\tfrac{3 \cdot 100}{4} %$, was $75\,%$ ergibt.

Mit dem Dreisatz

Grundwert = Prozentwert × 100 : Prozentsatz

umgestellt:

Prozentsatz = Prozentwert × 100 : Grundwert

Prozentwert = Grundwert × Prozentsatz : 100

Beispiele

Umsatzsteuer

Ein alltägliches Beispiel ist die Berechnung der Umsatzsteuer. Diese ist definiert durch den Wert eines Produktes (Nettobetrag) multipliziert mit einem Umsatzsteuersatz, der in Prozent angegeben wird. Der Grundwert dieser Prozentangabe ist also der Nettobetrag. Der Bruttobetrag ist die Summe von Nettobetrag und Umsatzsteuer:

Umsatzsteuer = Nettobetrag ∙ Umsatzsteuersatz

Bruttobetrag = Nettobetrag + Umsatzsteuer

Sind 100 Euro der Nettobetrag und der Umsatzsteuersatz beträgt 19 %, so errechnet man die Umsatzsteuer durch:

100 Euro ∙ 19 % = 19 Euro

was dasselbe ist wie

100 Euro ∙ 0,19 = 19 Euro

Demzufolge errechnet sich der Bruttobetrag:

100 Euro + 19 Euro = 119 Euro

Wenn man weiß, dass 19 % dasselbe ist wie 0,19 vom Ganzen, lässt sich leicht einsehen, dass der Bruttobetrag das 1,19-fache des Nettobetrages ist, also

Bruttobetrag = Nettobetrag ∙ 1,19

Deshalb lässt sich durch Umstellung dieser Formel aus dem Bruttobetrag der Nettobetrag einfach errechnen durch

Nettobetrag = Bruttobetrag / 1,19

Die im Bruttobetrag enthaltene Umsatzsteuer beträgt

Umsatzsteuer = Bruttobetrag - Nettobetrag

also

Umsatzsteuer = Bruttobetrag - Bruttobetrag / 1,19

Sprachgebrauch

• „Im Rechnungsbetrag sind 19 % Umsatzsteuer enthalten“

bedeutet, dass der Umsatzsteuersatz 19 % beträgt und der Rechnungsbetrag der Bruttobetrag ist, also Nettobetrag plus Umsatzsteuer. Korrekt müsste es daher lauten: „Im Rechnungsbetrag ist die Umsatzsteuer mit einem Umsatzsteuersatz von 19 % enthalten“.

• „Die Umsatzsteuer beträgt 19 %“

Falsch, sollte eigentlich heißen „der Umsatzsteuersatz beträgt 19 %“.

• „19 % des Rechnungsbetrages sind Umsatzsteuer“

Falsch (wenn der Umsatzsteuersatz 19 % beträgt), da es sich beim Rechnungsbetrag um den Nettowert plus Umsatzsteuer handelt. Von einem Betrag von beispielsweise 119 Euro sind 19 % gleich 22,61 Euro. Tatsächlich beträgt die enthaltene Umsatzsteuer hier aber 19 Euro und macht rund 15,97 % des Rechnungsbetrages aus.

Da 19 % und 15,97 % nicht weit auseinanderliegen, kann die falsche Formulierung zu unbemerkten Fehlern führen. Deshalb noch folgende Beispiele:

• „Mein Taschengeld hat sich um 50 % erhöht.“

Beträgt das Taschengeld nach der Erhöhung insgesamt 15 Euro, so sind 50 % hier gleich 5 Euro. „50 %“ bezieht sich auf den Grundwert 10 Euro. Das ist der Betrag des Taschengeldes vor der Erhöhung.

• „50 % meines Taschengeldes sind ein Zuschuss von meiner Oma.“

Beträgt das Taschengeld insgesamt 15 Euro, so sind 50 % hier gleich 7,50 Euro. „50 %“ bezieht sich hier auf den Grundwert 15 Euro. Obwohl der Prozentsatz „50 %“ in beiden Aussagen gleich ist, sind die Prozentwerte „5 Euro“ und „7,50 Euro“ unterschiedlich, da sich die Aussagen auf unterschiedliche Grundwerte beziehen.

Steigung in Prozent

10 % Steigung sind 10 m Höhenunterschied auf einer horizontalen Strecke von 100 m

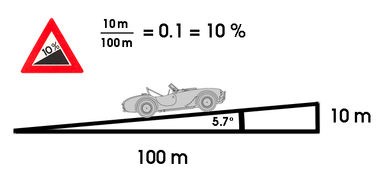
Im Straßenverkehr wird die Steigung (bzw. das Gefälle) in Prozent angegeben. Diese Prozentangabe drückt das Verhältnis von Höhenunterschied und waagerechter Strecke aus. Eine Steigung von 100 % bedeutet demzufolge einen Steigungswinkel von 45°. Eine Steigung von 10 % bedeutet, dass auf einer horizontalen Strecke von 100 m ein Höhenunterschied von 10 m zurückgelegt wird.

Finanzmathematik

In der Finanzmathematik wird das Symbol p in dieser Formel durch 100 geteilt. Damit will man die Umrechnung direkt in die Formel einbauen. Mathematisch betrachtet ist dies jedoch ein Rechenfehler bei der Umwandlung innerhalb eines Einheitensystems und ist nicht SI-Konform (siehe Umrechnung zwischen Zahlen- und Prozentwerten). Die Summe aller Prozentsätze p_x muss hierbei immer 1 (100 %) ergeben:

∑	px = 1
x

Die Summe aller Prozentwerte W_x ergibt den Grundwert:

∑	Wx = K
x

Eingabe am Taschenrechner

Taschenrechner unterschiedlicher Bauart und Hersteller behandeln die Tastatureingabe einer Prozentrechnung unterschiedlich. Dies kann zu Verwirrungen bzw. dazu führen, dass Benutzer von Taschenrechnern bei Prozentrechnungen auf die Prozenttaste verzichten und eher auf den Dreisatz oder auf die obenstehende Formel zurückgreifen.

Das Prozentzeichen

Das Prozent-Zeichen entstand aus „cto“, der italienischen Abkürzung für „cento“. Der obere Kreis war ursprünglich das „c“, der Schrägstrich das „t“ und der untere Kreis das „o“.

In der Informatik wird das %-Zeichen (zweckentfremdet) meist für die Operation Modulo verwendet oder zur Kennzeichnung von Sonderzeichen (URL-Kodierung) z. B. in Webadressen. In Suchalgorithmen und Abfragen wird es auch als Platzhalter für beliebige Zeichen in Datenfeldern gebraucht.

Siehe auch

• Volumenprozent
• Promille
• Prozentpunkt
• Prozentrang
• Parts per million (ppm)

Weblinks

Erhöhter und verminderter Grundwert

Quellen

1. ↑ Duden Fremdwörterbuch
2. ↑ Internationales Einheitensystem, SI-Broschüre, 8. Aufl. 2006, S. 46 bzw. 134 Online-Version (PDF-Datei, 3,9 MB)
3. ↑ Duden, Rechtschreibung der deutschen Sprache, Richtlinien für den Schriftsatz, Prozent- und Promillezeichen
4. ↑ Punkt 3.1.5, Tabelle 2 in der DIN 1333 - Ausgabe September 1992