- Abessinischen Bauernregel
-
Die Russische Bauernmultiplikation (auch Ägyptisches Multiplizieren oder Abessinische Bauernregel genannt) ist ein einfaches Verfahren zur Multiplikation zweier natürlicher Zahlen.
Es war schon im Altertum bekannt, in Deutschland wurde es bis ins Mittelalter verwendet. In Russland war es bis weit in die Neuzeit üblich, daher der Name.
Das Verfahren hat den Vorteil, dass man im Prinzip nur halbieren, verdoppeln und addieren können muss, das kleine Einmaleins wird nicht benötigt. Implizit wird eine schriftliche Multiplikation im Binärsystem durchgeführt.
Inhaltsverzeichnis
Verfahren
Beschreibung
Und so funktioniert das Verfahren:
- Man schreibt die beiden zu multiplizierenden Zahlen nebeneinander.
- Auf der linken Seite werden die Zahlen jeweils halbiert (Reste abgerundet) und die Ergebnisse untereinander geschrieben, bis man zur 1 gelangt.
- Auf der rechten Seite werden die Zahlen verdoppelt und untereinander geschrieben.
- Die rechts stehenden (verdoppelten) Zahlen werden gestrichen, wenn die links stehende Zahl gerade ist.
- Die Summe der nicht gestrichenen rechts stehenden Zahlen ergibt das gesuchte Produkt.
Beispiel: 27 mal 82
-
A-Seite B-Seite Dies addieren 27 82 82 13 164 164 6 328 — 3 656 656 1 1312 1312 Ergebnis: 2214
Algorithmus
Der folgende Algorithmus in Python soll die Funktion demonstrieren. In der Praxis eignet sich das Verfahren vor allem für die Rechnung mit binären Zahlen, da hier die Verdoppelung und die Halbierung durch eine einfache Bit-Verschiebung (left bzw. right shift) möglich ist:
def rusmul(a,b): """liefert das Produkt zweier natürlicher Zahlen a und b""" ergebnis = 0 while a > 0: rest = a % 2 # Modulo (Rest) if rest == 1: ergebnis = ergebnis + b a = a - 1 b = b << 1 # Verdopplung a = a >> 1 # Halbieren ohne Rest return ergebnis
Beispiele
35 · 89 35 89 17 178 8 3564 7122 14241 2848 Ergebnis 3115 84 · 123 84 12342 24621 492 10 9845 1968 2 39361 7872 Ergebnis 10.332 Beweis
Die Korrektheit der russischen Multiplikation kann durch vollständige Induktion bewiesen werden:
Bezeichne dazu RM(n, m) das Rechenverfahren und Ergebnis der russischen Multiplikation für die natürlichen Zahlen n und m.
- Induktionsanfang
- Für
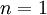 und jedes beliebige
und jedes beliebige 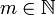 gilt:
gilt: 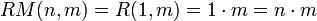 .
.
- Für
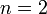 und jedes beliebige
und jedes beliebige 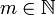 gilt:
gilt: 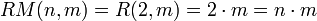 .
.
- Induktionsschritt
- Sei
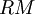 bereits bewiesen für
bereits bewiesen für 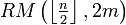 (Induktionsannahme).
(Induktionsannahme).
- Es gilt
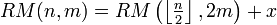 , wobei
, wobei 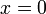 , wenn
, wenn 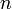 gerade ist und
gerade ist und 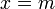 , wenn
, wenn 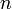 ungerade ist.
ungerade ist.
- Daraus folgt aufgrund der Induktionsannahme
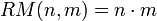 .
.
Analoges Verfahren: Binäre Exponentiation
Dieselbe Idee kann auch benutzt werden, um Potenzen mit großen ganzzahligen Exponenten zu berechnen: Der Exponent wird schrittweise halbiert und die Basis quadriert, am Ende werden die Potenzen mit ungeraden Exponenten aufmultipliziert. Dieses Verfahren heißt binäre Exponentiation.
Weblinks
- Eric W. Weisstein: Russian Multiplication auf MathWorld (englisch) und in WolframDemonstrationsProject (engl.)
Wikimedia Foundation.
