- Carl-Friedrich Gauss
-
Johann Carl Friedrich Gauß (latinisiert Carolus Fridericus Gauss; * 30. April 1777 in Braunschweig; † 23. Februar 1855 in Göttingen) war ein deutscher Mathematiker, Astronom, Geodät und Physiker mit einem breit gefächerten Feld an Interessen.
Seine überragenden wissenschaftlichen Leistungen waren schon seinen Zeitgenossen bewusst. Bereits 1856 ließ der König von Hannover Gedenkmünzen mit dem Bild von Gauß und der Inschrift Mathematicorum Principi (lat.: „dem Fürsten der Mathematiker“) prägen. Da Gauß nur einen Bruchteil seiner Entdeckungen veröffentlichte, erschloss sich der Nachwelt die Tiefgründigkeit und Reichweite seines Werks erst, als 1898 sein Tagebuch (s.u.) entdeckt und ausgewertet wurde.
Inhaltsverzeichnis
Leben
Carl Friedrich war das einzige Kind der Eheleute Gerhard Dietrich und Dorothea Gauß, geb. Benze. Die Mutter, eine nahezu analphabetische, jedoch in hohem Grade intelligente Tochter eines armen Steinmetzen, arbeitete zunächst als Dienstmädchen, bevor sie die zweite Frau von Gerhard Dietrich Gauß wurde. Dieser hatte viele Berufe, er war unter anderem Gärtner, Schlachter, Maurer, Kaufmannsassistent und Schatzmeister einer kleinen Versicherungsgesellschaft. Anekdoten besagen, dass bereits der dreijährige Carl Friedrich seinen Vater bei der Lohnabrechnung korrigierte. Später sagte er von sich selbst, er habe das Rechnen vor dem Sprechen gelernt. Sein Leben lang behielt er die Gabe, selbst komplizierteste Rechnungen im Kopf durchzuführen.
Im Alter von neun Jahren kam Gauß in die Volksschule. Dort stellte sein Lehrer Büttner seinen Schülern als Beschäftigung die Aufgabe, die Zahlen von 1 bis 100 zu summieren. Gauß hatte sie allerdings nach kürzester Zeit gelöst, indem er 50 Paare mit der Summe 101 bildete (1 + 100, 2 + 99, …, 50 + 51) und 5050 als Ergebnis erhielt. Die daraus resultierende Formel wird gelegentlich auch als „der kleine Gauß“ bezeichnet.
Dieses Ereignis ließ Gauß’ Lehrer seine außergewöhnliche mathematische Begabung erkennen, woraufhin er ein besonderes Rechenbuch aus Hamburg für ihn organisierte und unterstützt von seinem Assistenten Martin Bartels dafür sorgte, dass Gauß das Gymnasium Catharineum besuchen konnte. Als der Wunderknabe Gauß vierzehn Jahre alt war, wurde er dem Herzog Carl Wilhelm Ferdinand von Braunschweig bekannt gemacht. Dieser unterstützte ihn sodann finanziell und sorgte für seinen Lebensunterhalt. So konnte Gauß von 1792 bis 1795 am Collegium Carolinum studieren, das zwischen höherer Schule und Hochschule anzusiedeln ist und der Vorgänger der heutigen Technischen Universität in Braunschweig ist. Dort war es der Professor Eberhard August Wilhelm von Zimmermann, der sein mathematisches Talent erkannte, ihn förderte und ihm ein väterlicher Freund wurde.
Im Oktober 1795 wechselte Gauß an die Universität Göttingen. Dort hörte er bei Professor Heyne Vorlesungen über klassische Philologie, die ihn damals genauso wie die Mathematik interessierte. Letztere wurde durch Abraham Gotthelf Kästner, der zugleich Dichter war, repräsentiert. Bei Georg Christoph Lichtenberg hörte er im Sommersemester 1796 Experimentalphysik und sehr wahrscheinlich im folgenden Wintersemester Astronomie. In Göttingen schloss er Freundschaft mit Wolfgang Bolyai.
Im Alter von neunzehn Jahren gelang es Gauß als Erstem, die Konstruierbarkeit des regelmäßigen Siebzehnecks zu beweisen – eine sensationelle Entdeckung, denn seit der Antike gab es auf diesem Gebiet kaum noch Fortschritte. Dies war mit ein Grund, sich gegen Sprachen und Philosophie und für das Studium der Mathematik zu entscheiden, das er 1799 mit seiner Doktorarbeit an der Academia Julia (Universität in Helmstedt) abschloss. Die Mathematik war hier durch Johann Friedrich Pfaff gut vertreten, und nicht zuletzt legte Gauß’ Gönner, der Herzog von Braunschweig, Wert darauf, dass Gauß nicht an einer „ausländischen“ Universität promovierte.
Nach seiner Promotion lebte Gauß in Braunschweig von dem kleinen Gehalt, das ihm der Herzog zahlte, und arbeitete an seinem Werk Disquisitiones Arithmeticae.
Einen Ruf an die Petersburger Akademie der Wissenschaften lehnte Gauß ab: nämlich aus Dankbarkeit gegenüber seinem Gönner, dem Herzog von Braunschweig und wohl in der Hoffnung, dass dieser ihm eine Sternwarte in Braunschweig bauen würde. Nach dem plötzlichen Tod des Herzogs nach der Schlacht bei Jena und Auerstedt wurde Gauß im November 1807 Professor in Göttingen und Direktor der dortigen Sternwarte. Dort musste er Lehrveranstaltungen halten, gegen die er aber eine Abneigung entwickelte. Trotzdem wurden mehrere seiner Studenten einflussreiche Mathematiker, darunter Richard Dedekind und Bernhard Riemann.
Im November 1804 verlobte er sich mit Johanna Elisabeth Rosina Osthoff (* 1780; † 1809), der Tochter eines Weißgerbers aus Braunschweig, und heiratete sie am 9. Oktober 1805. Am 21. August 1806 wurde noch in Braunschweig das erste Kind geboren, Joseph, benannt nach dem Entdecker des Zwergplaneten Ceres, Giuseppe Piazzi. In Göttingen folgte 1808 die Tochter Wilhelmine, die am 12. August 1840 starb, und am 11. Oktober 1809 Louis, bei dessen Geburt seine Frau Johanna starb und der ihr am 1. März 1810 folgte. Ein Jahr darauf, am 4. August 1810, erfolgte die Heirat mit Friederica „Minna“ Wilhelmine, geb. Waldeck (* 1788; † 1831). Die Ehe war ebenfalls als glücklich zu bezeichnen[1], und die beiden hatten drei Kinder: Eugen (* 29. Juli 1811; † 1896), der die Rechte studierte und später nach Amerika auswanderte, um dort als Kaufmann zu leben; Wilhelm (* Oktober 1813; † 1883), der 1837 Eugen nachfolgte und ebenfalls nach Amerika auswanderte, um dort Landwirtschaft zu betreiben; und Therese (* Juni 1816; † 1864). Im Sommer 1818 begann Minna zu kränkeln, was sich später als Tuberkulose herausstellen sollte, und am 12. September 1831 verstarb sie. Von da an führte Tochter Therese den Haushalt.
Gauß’ Vater starb am 14. April 1808 in Braunschweig. Am 18. April 1839 verstarb die Mutter im Alter von 95 Jahren in Göttingen. Gauß selbst starb am 23. Februar 1855 morgens um 1 Uhr 5 Minuten in Göttingen. Heute liegt er dort auf dem Albanifriedhof (Cheltenham-Park) begraben, sein Gehirn jedoch wurde entnommen. Es wurde mehrfach mit verschiedenen Methoden, aber ohne besonderen Befund, der seine Rechenleistungen erklären würde, untersucht (zuletzt 1998).[2] Es befindet sich heute separat, in Formalin konserviert, in der Abteilung für Ethik und Geschichte der Medizin der Medizinischen Fakultät der Universität Göttingen. Viele seiner Entdeckungen teilte er in Briefen Freunden mit oder notierte sie in seinen Tagebüchern, die erst 1898 entdeckt wurden.
Als im Alter seine Schaffenskraft abnahm, beschäftigte er sich zunehmend mit Literatur, führte aber auch noch Listen über die monatlichen Einnahmen der Hannöverschen Staatseisenbahnen und die Lebenserwartung berühmter Männer (in Tagen gerechnet). So schrieb er am 7. Dezember 1853 an Alexander von Humboldt: „Es ist übermorgen der Tag, wo Sie, mein hochverehrter Freund, in ein Gebiet übergehen, in welches noch keiner der Koryphäen der exacten Wissenschaften eingedrungen ist, der Tag, wo Sie dasselbe Alter erreichen, in welchem Newton seine durch 30766 Tage gemessene irdische Laufbahn geschlossen hat.“
Gauß war zutiefst religiös und konservativ. Zudem war er sehr monarchistisch eingestellt, die Revolution von 1848 hieß er nicht gut.
Leistungen
Gauß misstraute bereits mit zwölf Jahren der Beweisführung in der elementaren Geometrie und ahnte mit sechzehn Jahren, dass es neben der euklidischen noch eine andere, nicht-euklidische Geometrie geben muss.
Mit achtzehn Jahren entdeckte er einige Eigenschaften der Primzahlverteilung und fand die Methode der kleinsten Quadrate, bei der es darum geht, die Summe der Quadrate von Abweichungen zu minimieren. Nach ihr lässt sich etwa das wahrscheinlichste Ergebnis für eine neue Messung aus einer genügend großen Zahl vorheriger Messungen ermitteln. Auf dieser Basis untersuchte er später Theorien zur Berechnung von Flächeninhalten unter Kurven (numerische Integration), die ihn zur gaußschen Glockenkurve gelangen ließen. Die zugehörige Funktion ist bekannt als die Standardnormalverteilung und wird bei vielen Aufgaben zur Wahrscheinlichkeitsrechnung angewandt, wo sie die (asymptotische, d. h. für genügend große Datenmengen) Verteilungsfunktion von zufällig um einen Mittelwert streuenden Daten ist. Gauß selber machte davon u. a. in seiner erfolgreichen Verwaltung der Witwen- und Waisenkasse der Göttinger Universität Gebrauch.
Als 19-Jähriger führte er 1796, bei Betrachtungen über die Bogenlänge auf einer Lemniskate in Abhängigkeit von der Entfernung des Kurvenpunktes zum Ursprung, mit den lemniskatischen Sinusfunktionen die historisch ersten, heute so genannten elliptischen Funktionen ein. Seine Notizen darüber hat er jedoch nie veröffentlicht. Diese Arbeiten stehen in Zusammenhang mit seiner Untersuchung des arithmetisch-geometrischen Mittels.
Gauß erfasste früh den Nutzen komplexer Zahlen, so auch in seiner Doktorarbeit von 1799, die einen strengeren Beweis des Fundamentalsatzes der Algebra enthielt. Dieser Satz besagt, dass jede algebraische Gleichung mit Grad größer als null mindestens eine reelle oder komplexe Lösung besitzt. Den älteren Beweis d’Alemberts kritisierte Gauß als ungenügend, aber auch sein eigener Beweis erfüllt noch nicht die späteren Ansprüche an topologische Strenge.
Am 29. März 1796, wenige Wochen vor seinem neunzehnten Geburtstag, bewies er die Konstruierbarkeit des regelmäßigen Siebzehnecks und lieferte damit die erste nennenswerte Ergänzung euklidischer Konstruktionen seit 2000 Jahren. Dies war aber nur ein Nebenergebnis bei der Arbeit für sein zahlentheoretisch viel weiterreichendes Werk Disquisitiones arithmeticae. Eine erste Ankündigung dieses Werkes fand sich am 1. Juni 1796 im Intelligenzblatt der allgemeinen Literatur-Zeitung in Jena. Die 1801 erschienenen Disquisitiones wurden grundlegend für die weitere Entwicklung der Zahlentheorie, zu der einer seiner Hauptbeiträge der Beweis des quadratischen Reziprozitätsgesetzes war, das die Lösbarkeit von quadratischen Gleichungen „mod p“ beschreibt und für das er im Laufe seines Lebens fast ein Dutzend verschiedene Beweise fand. Neben dem Aufbau der elementaren Zahlentheorie auf modularer Arithmetik findet sich auch eine Diskussion von Kettenbrüchen und der Kreisteilung, mit einer berühmten Andeutung über ähnliche Sätze bei der Lemniskate und anderen elliptischen Funktionen, die später Abel u. a. anregten. Einen Großteil des Werks nimmt die Theorie der quadratischen Formen ein, deren Geschlechtertheorie er entwickelt. Es finden sich aber noch viele weitere tiefliegende Resultate, oft nur kurz angedeutet, in diesem Buch, die die Arbeit späterer Generationen von Zahlentheoretikern in vielfältiger Weise befruchteten. Der Zahlentheoretiker Dirichlet berichtet, er hätte die Disquisitiones sein Leben lang bei der Arbeit stets griffbereit gehabt. Das gleiche gilt für seine beiden Arbeiten über biquadratische Reziprozitätsgesetze von 1825 und 1831, in denen er auch die Gaußschen Zahlen einführt (ganzzahliges Gitter in komplexer Zahlenebene). Beweise für diese Gesetze gab erst Eisenstein. Die Arbeiten sind wahrscheinlich Teil einer geplanten Fortsetzung der Disquisitiones, die aber nie erschien. André Weil regte die Lektüre dieser Arbeiten (und einiger Stellen im Tagebuch, wo es in versteckter Form um Lösung von Gleichungen über endlichen Körpern geht) nach seinen eigenen Angaben zu seinen Arbeiten über die Weil-Vermutungen an. Gauß kannte auch den Primzahlsatz, veröffentlichte ihn aber nicht.[3]
Nach der Fertigstellung der Disquisitiones wandte sich Gauß der Astronomie zu. Anlass hierfür war die Entdeckung des Zwergplaneten Ceres durch Giuseppe Piazzi am 1. Januar 1801, dessen Position man kurz nach seiner Entdeckung wieder verloren hatte. Der 24-jährige Gauß schaffte es, die Bahn mit Hilfe einer neuen indirekten Methode der Bahnbestimmung und seiner Ausgleichsrechnungen auf Basis der Methode der kleinsten Quadrate so zu berechnen, dass Heinrich Olbers ihn genau ein Jahr später, am 1. Januar 1802, wiederfinden konnte. Gauß beschäftigte sich danach auch noch mit der Bahn des Asteroiden Pallas, auf dessen Berechnung die Pariser Akademie ein Preisgeld ausgesetzt hatte, konnte die Lösung jedoch nicht finden. Seine Erfahrungen mit der Bahnbestimmung von Himmelskörpern mündeten in seinem Werk Theoria motus corporum coelestium in sectionibus conicis solem ambientium (Theorie der Bewegung der Himmelskörper, die die Sonne in Kegelschnitten umkreisen), das 1809 erschien. Diese Arbeiten machten Gauß mehr noch als seine Zahlentheorie in Europa mit einem Schlag bekannt.
In der Potentialtheorie und Physik ist das Gauß-Gesetz (1835, publiziert erst 1867) fundamental, das das Volumenintegral der Divergenz (Ableitungsvektor angewandt auf das Vektorfeld) eines Vektorfeldes mit dem Oberflächenintegral des Vektorfeldes um dieses Volumen herum in Beziehung setzt.
Um das Osterdatum für jedes beliebige Jahr rechnerisch ermitteln zu können, entwickelte er eine geschlossene Formel. Erstmals veröffentlicht wurde diese Berechnung in der von Freiherrn von Zach herausgegebenen Monatlichen Correspondenz zur Beförderung der Erd- und Himmels-Kunde, Band II, August 1800. Sie wurde nachgedruckt in den Gesammelten Werken, Band VI. In dem Artikel Noch etwas über die Bestimmung des Osterfestes, veröffentlicht am 12. September 1807 im Braunschweigischen Magazin, ging Gauß noch von einem Epaktensprung alle 300 Jahre aus. In der Zeitschrift für Astronomie und verwandte Wissenschaften wurde 1816 der Artikel Berichtigung zu dem Aufsatze: Berechnung des Osterfestes veröffentlicht, in dem Gauß eine Ergänzung seiner gaußschen Osterformel vornimmt, die den Epaktensprung alle 312,5 Jahre vorsieht.
 Der Gauß’sche Punkt in Bremen
Der Gauß’sche Punkt in BremenAuf dem Gebiet der Geodäsie sammelte Gauß zwischen 1797 und 1801 die ersten Erfahrungen, als er dem französischen Generalquartiermeister Lecoq bei dessen Landesvermessung des Herzogtums Westfalens als Berater zur Seite stand. Zum zweiten Mal kam er 1816 damit in Berührung, als ihn der König von Dänemark mit der Durchführung einer Breitengrad- und Längengradmessung in dänischem Gebiet beauftragte. Nach abschließenden Verhandlungen leitete Gauß dann zwischen 1818 und 1826 die Landesvermessung des Königreichs Hannover („gaußsche Landesaufnahme“). Durch die von ihm erfundene Methode der kleinsten Quadrate und die systematische Lösung umfangreicher linearer Gleichungssysteme (gaußsches Eliminationsverfahren) gelang ihm eine erhebliche Steigerung der Genauigkeit. Auch für die praktische Durchführung interessierte er sich; er erfand als Messinstrument das über Sonnenspiegel beleuchtete Heliotrop.
In diesen Jahren beschäftigte er sich – angeregt durch die Geodäsie und die Karten-Theorie – auch mit der Theorie der Differentialgeometrie der Flächen und führte u. a. die gaußsche Krümmung ein und bewies sein „Theorema egregium“, das die Winkelsumme in Dreiecken mit der Krümmung in Beziehung setzt. Es zeigt, dass die Krümmung durch lokale Größen gegeben ist und nicht von der Einbettung der Fläche in den dreidimensionalen Raum abhängt, also auch bei Abbildungen von Flächen aufeinander wie in der Kartenprojektion erhalten bleibt.
Unabhängig von János Bolyai und Lobatschewski bemerkte er, dass das Euklidische Parallelenaxiom nicht denknotwendig ist. Seine Gedanken zur nichteuklidischen Geometrie veröffentlichte er jedoch nicht, vermutlich aus Furcht vor dem Unverständnis der Zeitgenossen. Als ihm sein Studienfreund Wolfgang Bolyai, mit dem er korrespondierte, allerdings von den Arbeiten seines Sohnes János Bolyai berichtet, lobt er ihn zwar, kann es sich aber nicht verkneifen zu erwähnen, dass er selbst schon sehr viel früher darauf gekommen war („seine Arbeit zu preisen hieße mich selbst zu preisen“).[4] Er habe darüber nichts veröffentlicht um dem „Geschrei der Böotier“ zu entgehen.[5] Lobatschewskis Arbeiten fand Gauß so interessant, dass er noch in fortgeschrittenem Alter russisch lernte, um sie zu studieren.
 Gedenktafel auf dem Brocken
Gedenktafel auf dem BrockenDer allgemeinen Relativitätstheorie zufolge ist der Raum in kosmologischem Maßstab möglicherweise „nicht-euklidisch“ (und die Raum-Zeit sowieso, selbst der beschleunigte Fall eines Apfels wird in ihr durch deren Krümmung beschrieben, verursacht durch die Masse der Erde), d. h. gekrümmt, ähnlich wie die Oberfläche der Erde. Wolfgang Sartorius von Waltershausen berichtet,[6] Gauß habe bei Gelegenheit der Hannoverschen Landesvermessung empirisch nach einer Abweichung der Winkelsumme besonders großer Dreiecke vom Euklidischen Wert von 180° gesucht. Wie etwa bei dem Dreieck, das vom Brocken im Harz, dem Inselsberg im Thüringer Wald und dem Hohen Hagen bei Dransfeld gebildet wird. Seitenlängen: Brocken – 68 km – Hoher Hagen – 84 km – Inselberg – 106 km – Brocken. Die Vermessung durch Gauß ist belegt, die oben erwähnte Vermutung zur Motivation ist dagegen unsicher.[7] Max Jammer schrieb über das Ergebnis dieser gaußschen Messung: „Es braucht kaum eigens gesagt zu werden, daß er innerhalb der Fehlergrenze keine Abweichung von 180° entdeckte und daraus den Schluß zog, die Struktur des wirklichen Raumes sei, soweit die Erfahrung darüber eine Aussage erlaubt, Euklidisch.“ [8]
Zusammen mit Wilhelm Eduard Weber arbeitete er ab 1831 auf dem Gebiet des Magnetismus. Gauß erfand das Magnetometer und verband so 1833 seine Sternwarte mit dem physikalischen Institut. Dabei tauschte er über elektromagnetisch beeinflusste Kompassnadeln Nachrichten mit Weber aus; die erste (elektromagnetische) Telegrafenverbindung auf der Welt. Mit ihm zusammen entwickelte er auch das cgs-Einheitensystem, das später, 1881, auf einem internationalen Kongress in Paris zur Grundlage der elektrotechnischen Maßeinheiten bestimmt wurde. Gauß fand auch unabhängig die Kirchhoffschen Regeln für Stromkreise. Er organisierte ein weltweites Netz von Beobachtungsstationen (Magnetischer Verein), um das erdmagnetische Feld zu vermessen.
Gauß arbeitete auf vielen Gebieten, veröffentlichte seine Ergebnisse jedoch erst, wenn eine Theorie seiner Meinung nach komplett war. Dies führte dazu, dass er Kollegen gelegentlich darauf hinwies, dieses oder jenes Resultat schon lange bewiesen zu haben, es wegen der Unvollständigkeit der zugrundeliegenden Theorie oder der ihm zum schnellen Arbeiten fehlenden nötigen Heiterkeit nur noch nicht präsentiert zu haben. Kritiker warfen ihm vor, dass dies Ausdruck einer übertriebenen Geltungssucht war. Bezeichnenderweise besaß er ein Petschaft, das einen von wenigen Früchten behangenen Baum und das Motto Pauca sed matura (Weniges, aber Reifes) zeigte.
Tatsache ist, dass er ein intensiver Tagebuchschreiber war und dort auch viele seiner Resultate notierte. Nach seinem Tod wurden über zwanzig dieser Bände gefunden. So konnte belegt werden, dass er einen Großteil seiner behaupteten Leistungen tatsächlich erbracht hat. Es wird angenommen, dass nicht alle seiner Tagebücher erhalten sind.
Namensgeber
Von Gauß entwickelte Methoden oder Ideen, die seinen Namen tragen, sind:
- das gaußsche Eliminationsverfahren zur Diagonalisierung und Invertierung von Matrizen und damit zur Lösung von linearen Gleichungssystemen
- das gaußsche Fehlerfortpflanzungsgesetz
- das gaußsche Fehlerintegral
- der gaußsche Integralsatz, auch Satz von Gauß-Ostrogradski oder Divergenzsatz genannt, in der Vektoranalysis
- das gaußsche Gesetz in der Elektrostatik
- die gaußsche Krümmung in der Differentialgeometrie
- die gaußsche Osterformel, zur Berechnung des Osterdatums
- die gaußsche Wochentagsformel, zur Berechnung eines Wochentages anhand eines Datums
- die gaußsche Trapezformel, zur Berechnung einer Fläche aus Koordinaten durch Zerlegung in Dreiecke bzw. Trapeze
- das gaußsche Prinzip des kleinsten Zwanges in der Mechanik
- die gaußschen Quadraturformeln, numerisches Integrations-Verfahren (siehe auch Gauß-Quadratur)
- die Stützpunkte bei der Gauß-Quadratur (z. B. Gauß-Legendre-Integration) heißen Gaußpunkte
- die gaußsche Normalverteilung, auch gaußsche Glockenkurve genannt (die Glockenkurve schmückte, neben dem Portrait von Carl Friedrich Gauß platziert, von 1989 bis 2001 die 10-DM-Banknote der Bundesrepublik Deutschland)
- die gaußschen Zahlen, eine Erweiterung der ganzen Zahlen auf die komplexen Zahlen
- die gaußsche Zahlenebene als geometrische Deutung der Menge der komplexen Zahlen
- die Gaußklammer, eine Funktion, die Zahlen auf die nächstkleinere ganze Zahl abrundet
- der Gauß-Prozess, ein stochastischer Prozess
- das Lemma von Gauß, ein Schritt in einem seiner Beweise des quadratischen Reziprozitätsgesetzes
- Der kleine Gauß: Addition einer Reihe (gaußsche Summenformel)
Methoden und Ideen, die teilweise auf seinen Arbeiten beruhen, sind:
- der Satz von Gauß-Bonnet in der Differentialgeometrie
- das Gauß-Elling-Verfahren, ein Verfahren zur Flächenberechnung nach Koordinaten
- der Gauß-Jordan-Algorithmus, eine Weiterentwicklung des gaußschen Eliminationsverfahrens
- das Gauß-Krüger-Koordinatensystem und die Gauß-Krüger-Projektion
- das Gauß-Markow-Theorem über die Existenz eines BLUE-Schätzers in linearen Modellen
- die gaußsche Optik, eine mathematische Beschreibung der Ausbreitung von Laserlicht
- das Gauß-Newton-Verfahren, ein Verfahren zur Lösung nichtlinearer Gleichungen
- das Gauß-Seidel-Verfahren, ein Verfahren zur Lösung von linearen Gleichungssystemen
- das Gaußgewehr, Geschütz, das ein ferromagnetisches Projektil mittels (Elektro-)Magneten beschleunigt, ähnlich Linearmotor
Zu seinen Ehren benannt sind:
- Wissenschaft und Technik
- das Gauß, die veraltete cgs-Einheit der magnetischen Flussdichte im gaußschen Einheitensystem
- das Gaußsche Einheitensystem
- mehrere Forschungsschiffe, siehe Gauss (Schiff)
- der Gauß-Lehrstuhl an der Georg-August-Universität Göttingen
- die Carl-Friedrich-Gauß-Fakultät für Mathematik, Informatik, Wirtschafts- und Sozialwissenschaften der TU Braunschweig
- Natur
- der Gaußberg im Kaiser-Wilhelm-II.-Land in der Antarktis
- der Mondkrater Gauß
- der Asteroid Gaussia
- Gebäude
- der Gaußturm auf dem Hohen Hagen bei Dransfeld
- ca. zehn Schulen in Deutschland und weitere weltweit
- das Gauß IT Zentrum der TU Braunschweig
- Software
- das Numerikprogramm GAUSS
- das Computerchemieprogramm GAUSSIAN
- das Gauss-Projekt. eine Datenbank von Softwarepatenten
- Ehrungen
- die Carl-Friedrich-Gauß-Medaille der Braunschweigischen Wissenschaftlichen Gesellschaft
- die Gauß-Medaille in verschiedenen Ausführungen von 1977 der Akademie der Wissenschaften der DDR, die an verdiente Wissenschaftler verliehen wurde
- die festliche Gauß-Vorlesung der Deutschen Mathematiker-Vereinigung zu Facetten der Mathematik aus historischer und aktueller Perspektive (einmal pro Semester seit 2001 an wechselndem Ort)[9]
Schriften
- Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse (Neuer Beweis des Satzes, dass jede algebraische rationale ganze Funktion einer Veränderlichen in reelle Faktoren des ersten oder zweiten Grades zerlegt werden kann), C. G. Fleckeisen, Helmstadii (Helmstedt) 1799 (lateinisch; Doktorarbeit über den Fundamentalsatz der Algebra; bei der HU Berlin: [4]; auch in Carl Friedrich Gauß: Werke. Band 3, S. 3–30: [5], [6], [7])
- Disquisitiones Arithmeticae (Arithmetische Untersuchungen), Gerhard Fleischer jun., Lipsiae (Leipzig) 1801 (lateinisch; auch Carl Friedrich Gauß: Werke. Band 1)
- Theoria motus corporum coelestium in sectionibus conicis solem ambientium (Theorie der Bewegung der Himmelskörper, die die Sonne in Kegelschnitten umkreisen), F. Perthes und I. H. Besser, Hamburg 1809 (lateinisch; auch in Carl Friedrich Gauß: Werke. Band 7, S. 1–261)
- Theoria combinationis observationum erroribus minimis obnoxiae. Drei Abhandlungen betreffend die Wahrscheinlichkeitsrechnung als Grundlage des Gauß’schen Fehlerfortpflanzungsgesetzes, 1821 1823 1826 (lateinisch)
- Disquisitiones generales circa superficies curvas (Allgemeine Untersuchungen über gekrümmte Flächen), Commentationes Societatis Regiae Scientiarum Gottingensis recentiores 6 (classis mathematicae), 1828, S. 99–146 (lateinisch; bei Google Books: [8]; auch in Carl Friedrich Gauß: Werke. Band 4, S. 219–258)
- Principia generalia theoriae figurae fluidorum in statu aequilibrii (Allgemeine Grundlagen einer Theorie der Gestalt von Flüssigkeiten im Zustand des Gleichgewichts), Commentationes Societatis Regiae Scientiarum Gottingensis recentiores 7 (classis mathematicae), 1832, S. 39–88, und Dieterich, Göttingen 1830 (lateinisch; bei Google Books: [9]; auch in Carl Friedrich Gauß: Werke. Band 5, S. 31–77: [10])
- Dioptrische Untersuchungen, Abhandlungen der Mathematischen Classe der Königlichen Gesellschaft der Wissenschaften zu Göttingen 1, 1843, S. 1–34 (bei Google Books: [11]), und Dieterich, Göttingen 1841 (bei Gallica: [12]; auch in Carl Friedrich Gauß: Werke. Band 5, S. 245–276: [13])
- Untersuchungen über Gegenstände der höhern Geodaesie. Erste Abhandlung, Abhandlungen der Mathematischen Classe der Königlichen Gesellschaft der Wissenschaften in Göttingen 2, 1845, S. 3–34 (auch in Carl Friedrich Gauß: Werke. Band 4, S. 261–290)
- Untersuchungen über Gegenstände der höhern Geodäsie. Zweite Abhandlung, Abhandlungen der Mathematischen Classe der Königlichen Gesellschaft der Wissenschaften in Göttingen 3, 1847, S. 3–35 (auch in Carl Friedrich Gauß: Werke. Band 4, S. 303–334)
Briefwechsel und Tagebuch
- Christian August Friedrich Peters (Hrsg.): Briefwechsel zwischen C. F. Gauss und H. C. Schumacher, Gustav Esch, Altona 1860–1865 (bei Google Books: Band 1, 1+2, 2, 3+4, 3+4, 5+6)
- Karl Christian Bruhns (Hrsg.): Briefe zwischen A. v. Humboldt und Gauss, Wilhelm Engelmann, Leipzig 1877 (im Internet-Archiv: [14], [15], [16], [17])
- Briefwechsel zwischen Gauss und Bessel, Wilhelm Engelmann, Leipzig 1880 (im Internet-Archiv: [18])
- Franz Schmidt, Paul Stäckel (Hrsg.): Briefwechsel zwischen Carl Friedrich Gauss und Wolfgang Bolyai, B. G. Teubner, Leipzig 1899 (bei der University of Michigan: [19]; im Internet-Archiv: [20])
- Clemens Schaefer (Hrsg.): Briefwechsel zwischen Carl Friedrich Gauß und Christian Ludwig Gerling, Otto Elsner, Berlin 1927
- Mathematisches Tagebuch 1796–1814 (5. Auflage), Harri-Deutsch-Verlag, Frankfurt am Main 2005, ISBN 3-8171-3402-9 (mit Anmerkungen von Hans Wußing und Olaf Neumann)
- Jeremy Gray: A commentary on Gauss’s mathematical diary, 1796–1814, Expositiones Mathematicae 2, 1984, S. 97–130 (englisch)
Gesamtausgabe
- Carl Friedrich Gauß: Werke, herausgegeben von der (Königlichen) Gesellschaft der Wissenschaften zu Göttingen
- Band 1 bis 6, Dieterich, Göttingen 1863–1874 (bei Google Books: Band 2, 3, 3, 3, 5; im Internet-Archiv: Band 4, 6), zweiter Abdruck 1870–1877 (im Internet-Archiv: Band 1, 2, 3, 3, 4, 5, 5)
- Band 7 bis 12, B. G. Teubner, Leipzig 1900–1917, Julius Springer, Berlin 1922–1933 (im Internet-Archiv: Band 7, 10.2(1+5), 10.2(4))
In den Bänden 10 und 11 finden sich ausführliche Kommentare von Paul Bachmann (Zahlentheorie), Ludwig Schlesinger (Funktionentheorie), Alexander Ostrowski (Algebra), Paul Stäckel (Geometrie), Oskar Bolza (Variationsrechnung), Philipp Maennchen (Gauß als Rechner), Harald Geppert (Mechanik, Potentialtheorie), Andreas Galle (Geodäsie), Clemens Schaefer (Physik) und Martin Brendel (Astronomie). Herausgeber war zuerst Ernst Schering, dann Felix Klein.
Übersetzungen
- Recherches générales sur les surfaces courbes, Bachelier, Paris 1852 (französische Übersetzung von Disquisitiones generales circa superficies curvas, 1828; bei Gallica: [21])
- Theory of the Motion of the Heavenly Bodies Moving about the Sun in Conic Sections, Little, Brown and Company, Boston 1857 (englische Übersetzung von Theoria motus corporum coelestium in sectionibus conicis solem ambientium, 1809, von Charles Henry Davis; bei Google Books: [22], [23])
- Hermann Maser (Hrsg.): Carl Friedrich Gauss’ Untersuchungen über höhere Arithmetik, Julius Springer, Berlin 1889 (deutsche Übersetzung von Disquisitiones Arithmeticae, 1801; im Internet-Archiv: [24]); ; als Buch lieferbar: ISBN: ISBN: 978-3-941300-09-5, www.VerlagKessel.de
- Albert Wangerin (Hrsg.): Allgemeine Flächentheorie (Disquisitiones generales circa superficies curvas), Wilhelm Engelmann, Leipzig 1889 (deutsche Übersetzung; bei der University of Michigan: [25])
- Eugen Netto (Hrsg.): Die vier Gauss’schen Beweise für die Zerlegung ganzer algebraischer Funktionen in reelle Factoren ersten oder zweiten Grades (1799–1849), Wilhelm Engelmann, Leipzig 1890 (deutsche Übersetzung; bei der University of Michigan: [26]; im Internet-Archiv: [27])
- Eugen Netto (Hrsg.): Sechs Beweise des Fundamentaltheorems über quadratische Reste von Carl Friedrich Gauss, Wilhelm Engelmann, Leipzig 1901 (deutsche Übersetzung mit Anmerkungen; bei der University of Michigan: [28])
- General investigations of curved surfaces of 1827 and 1825, The Princeton University Library, 1902 (englische Übersetzung von Disquisitiones generales circa superficies curvas, 1828 und Neue allgemeine Untersuchungen über die krummen Flächen, 1901 von James Caddall Morehead und Adam Miller Hiltebeitel; bei der University of Michigan: [29])
Kartenwerke
- August Papen: Topographischer Atlas des Königreichs Hannover und Herzogthums Braunschweig, nach einem Maasstabe von 1/100.000 der wahren Länge, auf den Grund der von dem Geheimen Hofrath Gauss geleiteten vollständigen Triangulirung, aus den grossen topographischen Landes Aufnahmen und mehreren anderen Vermessungen reducirt und bearbeitet von A. Papen, Hannover 1832–1847.
Denkmäler
 Briefmarke (1955) zum 100. Todestag
Briefmarke (1955) zum 100. Todestag- Statue für Braunschweig (Inselwall/Schubertstraße), 1880, nach Entwurf von Fritz Schaper, ausgeführt von Hermann Heinrich Howaldt.
- Gauß-Weber-Denkmal in Göttingen, das Gauß zusammen mit Wilhelm Weber zeigt.
- Drei Göttinger Gedenktafeln.
- Gauß-Denkmal in Berlin (Kriegsverlust, nicht erneuert)
- Auf der „10 DM“-Banknote der vierten Serie der Deutschen Mark ist eine Abbildung Gauß’ zusammen mit einer Darstellung der Glockenkurve und wichtiger Gebäude Göttingens zu finden. An ihn erinnern ebenso zwei Sondermünzen, die 1977 aus Anlass seines 200. Geburtstages in der Bundesrepublik Deutschland (5 DM) und in der DDR (20 M) herausgegeben wurden.
- In Deutschland erinnern drei Briefmarken an Gauß: 1955 gab die Deutsche Bundespost aus Anlass seines 100. Todestages eine 10-Pf-Briefmarke heraus; 1977 erinnerte die DDR mit einer 20-Pf-Briefmarke an den 200. Geburtstag, ebenso die Deutsche Bundespost mit einer 40-Pf-Briefmarke
- Gedenktafel am Standort des Geburtshauses Wilhelmstraße 30 in Braunschweig.
- Gaußstein oberhalb der Ruine von Burg Lichtenberg bei Salzgitter-Lichtenberg
- Am 12. September 2007 wurde eine von Georg Arfmann geschaffene Gauß-Büste in der Gedenkstätte Walhalla enthüllt.[10]
Bildnisse
Von Gauß gibt es relativ viele Bildnisse, unter anderem:
- 17?? Silhouette aus den Jugendjahren
- 1803 Portrait (Ölgemälde) von Johann Christian August Schwarz (1755/56–1814)[11]
- 1810 Büste von Friedrich Künkler
- 18?? Zeichnung von Johann Benedict Listing (1808–1882)
- 1828 Lithographie von Siegfried Detlev Bendixen (1786–1864)
- 1840 Ölgemälde des dänischen Malers Christian Albrecht Jensen. Ort: Sternwarte Pulkowa in St. Petersburg
- 18?? Lithographie von Eduard Ritmüller (1805–1869) Gauss auf der Terrasse der Göttinger Sternwarte
- 1850 Altersbildnis 1 (Stahlstich?)
- 1854 Altersbildnis 2 (Stahlstich?)
- 1855 Daguerreotypie auf dem Totenbett von Philipp Petri (1800–1868)
- 1887 Kopie des Portraits von Jensen (1840) von Gottlieb Biermann. Ort: Hörsaal der Göttinger Sternwarte
Literatur
- Felix Klein: Gauß, erstes Kapitel der Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert, Julius Springer, Berlin 1926, S. 6–62 (Reprint: Springer-Verlag, Berlin Heidelberg New York 1979, ISBN 3-540-09234-X)
- Hans Wußing: Carl Friedrich Gauß, Biographien hervorragender Naturwissenschaftler, Techniker und Mediziner Band 15, BSB B. G. Teubner Verlagsgesellschaft 1. Auflage 1973, 5. Aufl. 1989, ISBN 3-322-00682-4
- Walter Kaufmann-Bühler: Gauß – eine biographische Studie, Springer-Verlag, 1987
- Kurt-R. Biermann (Hrsg.): Gauß in Gesprächen und Briefen, Urania Verlag und Beck Verlag, 1990
- Karin Reich: Gauß 1777–1977, Moos, München 1977
- Hans Reichardt (Hrsg.): C. F. Gauß: Gedenkband anläßlich des 100. Todestages am 23. Februar 1955, B. G. Teubner, Leipzig 1957 (mit Beiträgen von Kähler, H. Salié, Georg-Johann Rieger, Kochendörffer, Blaschke, Klingenberg, Markuschewitsch, K. Schröder, Gnedenko und Falkenhagen)
- Waldo Dunnington: Gauß – Titan of Science, Mathematical Association of America, 2003 (zuerst 1955. Dunnington trug viel Material zusammen)
- Ludwig Bieberbach: Carl Friedrich Gauß. Ein deutsches Gelehrtenleben, Keil-Verlag, Berlin 1938
- Hubert Mania: Gauß. Eine Biografie, Rowohlt, Reinbek bei Hamburg 2008, ISBN 3-498-04506-7
- Kenneth May: Gauß, Dictionary of Scientific Biography Bd. 5, 1972
- Mitteilungen der Gauß-Gesellschaft, Göttingen, seit 1964, Inhaltsverzeichnis
- Heinrich Rubner (Hrsg.), Rudolf Wagner, Carl Friedrich Gauß et al.: Gespräche mit Carl Friedrich Gauß in den letzten Monaten seines Lebens. Nachrichten der Akademie der Wissenschaften in Göttingen, Philologisch-Historische Klasse, Jahrgang 1975, Nr. 6. Vandenhoeck und Ruprecht, Göttingen 1975
- Moritz Cantor: Gauß: Karl Friedrich G.. In: Allgemeine Deutsche Biographie (ADB). Band 8, Duncker & Humblot, Leipzig 1878, S. 430–445.
- Zusätze und Berichtigungen. In: Allgemeine Deutsche Biographie (ADB). Band 8, Duncker & Humblot, Leipzig 1878, S. 796.
- Nikolai Stuloff: Gauß. Carl Friedrich. In: Neue Deutsche Biographie (NDB). Band 6, Duncker & Humblot, Berlin 1964, S. 101–107.
- Wilhelm Blaschke: Über die Differenzialgeometrie von Gauß, Jahresbericht der DMV 52, 1942, S. 61–71
Belletristik mit Bezug auf Carl Friedrich Gauß
- Daniel Kehlmann: Die Vermessung der Welt (Roman), Rowohlt, Reinbek bei Hamburg 2005, ISBN 3-498-03528-2
Weblinks
- Literatur von und über Carl Friedrich Gauß im Katalog der Deutschen Nationalbibliothek
- Gauß-Biographie auf der Homepage der Fa. Carl-Zeiss
- Gauß und Nachkommen (englisch)
Einzelnachweise
- ↑ Mathematiker-Biographien [1] (abgerufen am 15. Juli 2008)
- ↑ Wolfgang Hänicke, Jens Frahm und Axel D. Wittmann: Magnetresonanz-Tomografie des Gehirns von Carl Friedrich Gauß. In: MPI News 5, Heft 12 (1999). Online-Fassung (abgerufen am 12. August 2006)
- ↑ Er findet sich 1849 in einem Brief an Encke. Werke Bd. 10, Teil 1
- ↑ Brief an Wolfgang Bolyai, 6. März 1832, Werke Bd.8, S.220/221, [2]
- ↑ Brief an Bessel 21. Januar 1829. Böotier ist sprichwörtlich für plumpes Bauernvolk
- ↑ Gauß zum Gedächtnis, 1856
- ↑ Erhard Scholz hält es für durchaus möglich, dass Gauß daran dachte, sein preprint ist hier: [3]. Gauss selber äußert sich in einem Brief an Olbers vom 1. März 1827, zitiert bei Bühler S. 97, dahingehend, dass die Meßfehler für ein solches Feststellen von Abweichungen zu groß sind.
- ↑ Max Jammer: Das Problem des Raumes, Darmstadt 1960, S. 164
- ↑ Archiv der Gauß-Vorlesungen bei der Deutschen Mathematiker-Vereinigung
- ↑ Gauß-Büste in der Walhalla aufgestellt. Pressemitteilung der Stadt Göttingen vom 12. September 2007
- ↑ A. Wietzke: Das wieder aufgefundene Jugendbild von Carl Friedrich Gauß, Jahresbericht der DMV 41 (Angelegenheiten), 1932, S. 1–2
Personendaten NAME Gauß, Carl Friedrich ALTERNATIVNAMEN Gauß, Johann Carl Friedrich; Gauss, Carolus Fridericus (latinisiert) KURZBESCHREIBUNG deutscher Mathematiker, Astronom, Geodät und Physiker GEBURTSDATUM 30. April 1777 GEBURTSORT Braunschweig STERBEDATUM 23. Februar 1855 STERBEORT Göttingen
Wikimedia Foundation.

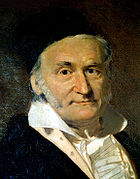
.jpg)




.JPG)

