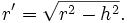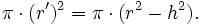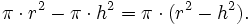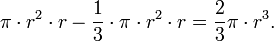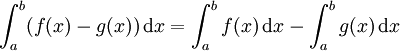Cavalieri-Prinzip

Die beiden Türme haben dasselbe Volumen, weil sie schichtweise dasselbe Volumen haben

Das Prinzip von Cavalieri (auch bekannt als der Satz des Cavalieri oder Cavalierisches Prinzip) ist eine Aussage aus der Geometrie, die auf den italienischen Mathematiker Bonaventura Cavalieri zurückgeht.

Prinzip von Cavalieri

Das Prinzip von Cavalieri besagt:

Zwei Körper besitzen dasselbe Volumen, wenn ihre Schnittflächen mit Ebenen parallel zu einer Grundebene in entsprechenden Höhen den gleichen Flächeninhalt haben.^[1]

Eine andere Formulierung lautet:

Liegen zwei Körper zwischen zueinander parallelen Ebenen E₁ sowie E₂ und werden sie von jeder zu diesen parallelen Ebene E' so geschnitten, dass gleich große Schnittflächen entstehen, so haben die Körper das gleiche Volumen.

Einordnung und Geschichte

In der modernen Herangehensweise über analytische Geometrie und Maßtheorie ist das Prinzip von Cavalieri ein Spezialfall des Satzes von Fubini. Cavalieri selbst hatte keinen strengen Beweis für das Prinzip, nutzte es jedoch als Rechtfertigung seiner Methode der Indivisibilien, die er 1635 in Geometria indivisibilibus und 1647 in Exercitationes Geometricae vorstellte. Hiermit konnte er für einige Körper die Volumen berechnen und über die Resultate von Archimedes und Kepler hinausgehen. Die Idee, das Berechnen von Volumina auf Flächen zurückzuführen, stellte einen wichtigen Schritt in der Entwicklung der Integralrechnung dar.

Aus dem Prinzip von Cavalieri lässt sich herleiten, dass das Volumen eines 'höhengedehnten' Körpers (bei gleichbleibender Grundfläche) proportional zu seiner Höhe ist. Als Beispiel: Ein Körper, dessen Höhe auf diese Weise verdoppelt wird, kann durch 2 gleiche Ausgangskörper konstruiert werden, indem zuerst alle äquivalenten Schnittflächen zusammengelegt werden und diese in der entsprechenden Reihenfolge des Ausgangskörpers aufgeschichtet werden (beide Ausgangskörper werden quasi ineinandergeschoben).

Anwendungsbeispiele

Zylinder

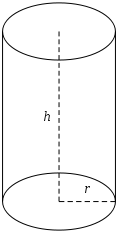
Zylinder

Die Schnitte eines Zylinders mit Ebenen senkrecht zur Rotationsachse sind Kreisscheiben mit Flächeninhalt πr², wenn r den Radius der Grundfläche bezeichnet. Nach dem Prinzip von Cavalieri ist das Volumen des Zylinders gleich dem eines Quaders derselben Höhe h, dessen Grundfläche denselben Flächeninhalt hat, also beispielsweise die Kantenlängen r und πr hat. Das Volumen des Zylinders ist demnach $\pi r^2\cdot h$.

Halbkugel

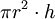Vertikale (oben) und horizontale (unten) Schnitte durch Halbkugel und Vergleichskörper

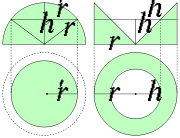
Der Schnitt einer Halbkugel vom Radius r mit einer Ebene, die in der Höhe h parallel zur Grundfläche verläuft, ist nach dem Satz des Pythagoras ein Kreis mit Radius

$r'=\sqrt{r^2-h^2}.$

Der Flächeninhalt der Schnittfläche ist demnach

$\pi\cdot(r')^2=\pi\cdot(r^2-h^2).$

Der Vergleichskörper ist in diesem Beispiel ein Zylinder mit derselben Grundfläche und Höhe wie die Halbkugel, aus dem ein auf der Spitze stehender Kreiskegel herausgeschnitten wurde. Die Schnittfläche in der Höhe h ist ein Kreisring mit äußerem Radius r und innerem Radius h, der Flächeninhalt ist also ebenfalls

$\pi\cdot r^2-\pi\cdot h^2=\pi\cdot(r^2-h^2).$

Also erfüllen die beiden Körper das Prinzip von Cavalieri und haben daher dasselbe Volumen. Das Volumen des Vergleichskörpers ist die Differenz der Volumina von Zylinder und Kegel, also

$\pi\cdot r^2\cdot r-\frac13\cdot\pi\cdot r^2\cdot r=\frac23\pi\cdot r^3.$

Verdoppelung liefert die bekannte Formel für das Kugelvolumen.

Bezug zur Integralrechnung

Differenz der Integrale und Integral der Differenz

Die Idee hinter dem Prinzip von Cavalieri findet sich vielfach in der Integralrechnung wieder. Ein Beispiel für um eins kleinere Dimensionen, also Längen der Schnitte von Geraden mit zwei Flächen, stellt die Gleichung

$\int_a^b(f(x)-g(x))\,\mathrm dx=\int_a^bf(x)\,\mathrm dx-\int_a^bg(x)\,\mathrm dx$

dar, die im Wesentlichen besagt, dass die Fläche A₁ zwischen den Funktionsgraphen von f und g genauso groß ist wie die Fläche A₂ unter dem Funktionsgraphen der Differenz 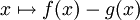$x\mapsto f(x)-g(x)$; diese letztere Fläche ist aber gerade dadurch charakterisiert, dass ihre senkrechten Schnitte dieselbe Länge haben wie die Schnitte von A₁.

In der modernen theoretischen Herangehensweise wird der Bezug zwischen Integral und Flächeninhalt bzw. Volumen jedoch typischerweise anders hergestellt; das Prinzip von Cavalieri ist dabei weniger wichtig.

Bezug zur Maßtheorie

Der Satz von Cavalieri in der oben beschriebenen elementaren Form ist ein Spezialfall des allgemeineren Satzes:

Sei 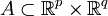$A \subset \mathbb R^p \times \mathbb R^q$ messbar. Dann sind auch 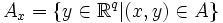$A_x = \{y \in \mathbb R^q | (x,y) \in A\}$ und $A^y = \{x \in \mathbb R^p | (x,y) \in A \}$

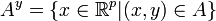
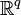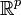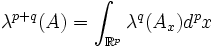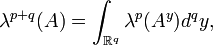für fast alle x bzw. y messbar (über $\mathbb R^q$ bzw. $\mathbb R^p$) und es gilt $\lambda^{p+q}(A) = \int_{\mathbb R^p} \lambda^q(A_x) d^p x$ bzw. $\lambda^{p+q}(A) = \int_{\mathbb R^q} \lambda^p(A^y) d^q y,$ wobei λ^k das k-dimensionale Lebesgue-Maß (Volumen) bezeichne. Insbesondere gilt: Ist 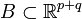$B \subset \mathbb R^{p+q}$ ebenfalls messbar und gilt λ^q(A_x) = λ^q(B_x) für fast alle x, so ist λ^{p + q}(A) = λ^{p + q}(B). Entsprechendes gilt für A_y und B_y.

Anmerkungen

1. ↑ Diese Bedingung beinhaltet auch, dass die beiden Körper dieselbe Höhe haben.

Weblinks

• Java-Applet zum Cavalieri-Prinzip von Walter Fendt