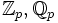Cayleyzahl

Die Oktaven, auch Oktonionen oder Cayleyzahlen, sind eine Verallgemeinerung der Quaternionen und besitzen das Mengensymbol 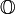$\mathbb{O}$. Sie entstehen durch die Anwendung des Verdopplungsverfahrens aus den Quaternionen.

Geschichte

Die Oktonionen wurden im Jahr 1843 von John Graves in einem Brief an William Rowan Hamilton zum ersten Mal beschrieben. Unabhängig davon wurden sie 1845 von Arthur Cayley veröffentlicht.

Multiplikationstabelle

Die Oktonionen sind eine 8-dimensionale Algebra über den reellen Zahlen. Eine mögliche Multiplikation ist – mit der Basis (1,i,j,k,l,m,n,o) – wie folgt gegeben:

$\begin{matrix} i^2=j^2=k^2=l^2=m^2=n^2=o^2=-1\\ i=jk=lm=on=-kj=-ml=-no\\ j=ki=ln=mo=-ik=-nl=-om\\ k=ij=lo=nm=-ji=-ol=-mn\\ l=mi=nj=ok=-im=-jn=-ko\\ m=il=oj=kn=-li=-jo=-nk\\ n=jl=io=mk=-lj=-oi=-km\\ o=ni=jm=kl=-in=-mj=-lk \end{matrix}$

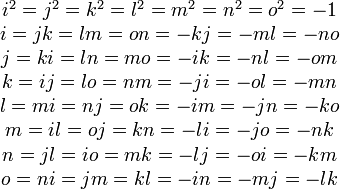
Daraus errechnet sich das Produkt der Einheiten

ijklmno = − 1

Eigenschaften

Die Oktonionen sind eine Divisionsalgebra mit Einselement.

Sie bilden keinen Schiefkörper (und damit auch keinen Körper), denn sie verletzen das

Assoziativgesetz der Multiplikation: $a \cdot ( b \cdot c ) = ( a \cdot b ) \cdot c$.

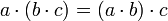Es gilt jedoch für alle Oktaven a und b:

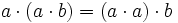$a \cdot ( a \cdot b ) = ( a \cdot a ) \cdot b$ und $a \cdot ( b \cdot b ) = ( a \cdot b ) \cdot b$.

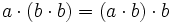Diese Eigenschaft wird Alternativität genannt. Die Oktonionen bilden einen Alternativkörper.

Aus der Alternativität folgt die Beziehung

$a \cdot (b \cdot a) = ( a \cdot b ) \cdot a$.

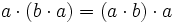Diese Beziehung wird auch Flexibilitätsgesetz genannt.

Die Oktonionen erfüllen außerdem die schärferen Moufang-Identitäten

$[a \cdot (b \cdot a)] \cdot c = a \cdot [b \cdot (a \cdot c)]$

und

$(a \cdot b) \cdot (c \cdot a) = a \cdot [(b \cdot c) \cdot a]$

Anwendung des Verdopplungsverfahrens auf die Oktaven liefert die Sedenionen.

Darstellungen

Jede Oktave kann dargestellt werden ...

... als 8er-Tupel von reellen Zahlen:

$(r_1, r_2, \ldots, r_8)$

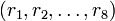
... als 4er-Tupel von komplexen Zahlen:

(c₁,c₂,c₃,c₄)

... als geordnetes Paar von Quaternionen:

(h₁,h₂)

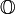Der Körper der reellen Zahlen $\mathbb{R}$ kann als Unterstruktur von $\mathbb{O}$ betrachtet werden:

Für alle Zahlen r aus $\mathbb{R}$ gilt:

r entspricht $(r, 0, \ldots , 0)$

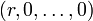
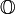Der Körper der komplexen Zahlen $\mathbb C$ kann als Unterstruktur von $\mathbb{O}$ betrachtet werden:

Für alle Zahlen c aus $\mathbb C$ gilt:

c entspricht (c,0,0,0)

Der Schiefkörper der Quaternionen 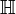$\mathbb H$ kann als Unterstruktur von 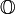$\mathbb{O}$ betrachtet werden:

Für alle Zahlen h aus 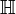$\mathbb H$ gilt:

h entspricht (h,0)

Für die Oktaven sind Addition und Multiplikation so definiert, dass sie abwärtskompatibel sind, das heißt ...

... für alle reellen Zahlen r und s gilt:

r + s = (r,0,...,0) + (s,0,...,0)

$r \cdot s = (r, 0, ... , 0) \cdot (s, 0, ... ,0)$

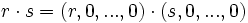
... für alle komplexen Zahlen c und d gilt:

c + d = (c,0,0,0) + (d,0,0,0)

$c \cdot d = (c, 0, 0, 0) \cdot (d, 0, 0, 0)$

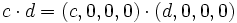
... für alle Quaternionen h und i gilt:

h + i = (h,0) + (i,0)

$h \cdot i = (h, 0) \cdot (i, 0)$

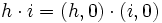
Literatur

• Ebbinghaus et. al.: Zahlen. Berlin: Springer, 1992, ISBN 3-54055-654-0
• Bartel Leendert van der Waerden, A history of Algebra, Springer-Verlag Heidelberg.
• Ruth Moufang, Zur Struktur von Alternativkörpern, Math. Ann. 110(1934)416.
• John Baez, The Octonions, Bull. Amer. Math. Soc. 39 (2002), 145-205. Online HTML version at http://math.ucr.edu/home/baez/octonions/.
• John Conway and Derek Smith, On Octonions and Quaternions, A K Peters, Natick, MA (2003). ISBN 1-56881-134-9.

Verwandte Themen

Hyperkomplexe Zahlen:

• Biquaternion
• Quaternion
• Sedenion

Zahlenbereiche

Natürliche Zahlen $\mathbb{N}$ | Ganze Zahlen $\mathbb{Z}$ | Rationale Zahlen $\mathbb{Q}$ | Reelle Zahlen $\mathbb{R}$ | Komplexe Zahlen $\mathbb C$ | Quaternionen $\mathbb H$ | Oktaven $\mathbb{O}$

p-adische Zahlen $\mathbb{Z}_p,\mathbb Q_p$