Chess engine

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h

Zweidimensionales Schachbrett, wie es viele Schach-Frontends auf dem Bildschirm ausgeben.

Ein Schachprogramm ist ein Computerprogramm zum Spielen von Schach. Es läuft entweder auf Allzweckcomputern wie PCs als ein Programm unter vielen oder in speziell zum Schachspielen angefertigten Schachcomputern. Die Entwicklung von Schachprogrammen ist eine Disziplin des Computerschachs.

Im engeren Sinne wird unter dem Schachprogramm nur die so genannte Engine für die Berechnung der Züge verstanden. Ein Schach-Frontend übernimmt dann deren Darstellung und die Benutzerinteraktion. Für die Kommunikation zwischen Schachengine und Frontend gibt es zwei weit verbreitete offene Schach-Kommunikationsprotokolle. Einmal das XBoard-Protokoll und das neuere Universal Chess Interface (UCI). Die Stellungen und Partien werden in proprietären Formaten oder auch im offenen PGN-Format gespeichert.

Aktuelle Programme

Als eines der bekanntesten kostenlos erhältlichen Schachprogramme gilt das Open-Source-Projekt Crafty von Robert Hyatt. Ein weiteres spielstarkes Schachprogramm ist Fruit, das bei der Weltmeisterschaft im Computerschach 2005 den zweiten Platz belegte. Bis zur Version 2.1 ist Fruit ebenfalls unter einer Open-Source Lizenz erhältlich, genauso wie das ungefähr gleich starke Glaurung 2.1. Eine Vorversion des Programmes Zappa, das die Weltmeisterschaft 2005 überlegen gewinnen konnte, steht lediglich als Freeware im Internet zur Verfügung, wie auch das Schachprogramm Spike von Volker Böhm und Ralf Schäfer. Das stärkste kostenlos erhältliche Programm ist momentan die Version 2.2n2 des Schachprogrammes Rybka, die auf einem 64-bit System mit einem Prozessor stärker als fast alle anderen Programme (auch kommerzielle) spielt. Für Anfänger bietet sich eine skalierbare Engine an, die man in der Elo-Stärke begrenzen kann wie Ufim.

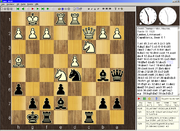José-Schachdatenbank und Schach-Frontend

Zur komfortablen Bedienung wird noch eine als Schach-Frontend bezeichnete Benutzeroberfläche benötigt. Hierzu kann beispielsweise das Programm XBoard genutzt werden. Es läuft unter den Betriebssystemen Windows (unter dem Namen WinBoard), Unix/Linux und Amiga und wird zusammen mit GNU Chess ausgeliefert. Auch das ebenfalls unter der GPL veröffentlichte José, ein graphisches java-basierendes Schach-Frontend mit Datenbankfunktionen, ist sehr gut. Das Schach-Frontend von KDE ist Knights.

Eine weitere beliebte Benutzeroberfläche unter Windows für mehr als 250 Schachprogramme ist Arena, die als Freeware verfügbar ist. Es gibt auch weitere Freeware die sich für den Einsteiger hervorragend eignet, so beispielsweise Arasan.

Ambitionierte Spieler greifen oft zu kommerziellen Programmen, die neben dem reinen Schachspiel auch viele Zusatzmöglichkeiten bieten, wie beispielsweise Partieanalyse und Schachtraining. Sehr bekannt dürften die Programme Shredder und Fritz sein. Diese Programme werden unter anderem von der Hamburger Firma ChessBase vertrieben, die den (europäischen) Markt für professionelle Schachsoftware zunehmend beherrscht. Seit 2005 schreibt das Programm Rybka Schlagzeilen in Fachzeitschriften und Computerforen. Rybka hat ausgeprägte Fertigkeiten auf positionellem beziehungsweise schachstrategischem Terrain und ist damit der menschlichen Spielweise näher gekommen als die übrigen Schachprogramme. Rybka führt auch die wichtigsten Computerschach-Ranglisten deutlich an (mit 50-150 Punkten Vorsprung) und Top-GM wie Anand, Topalov oder Morozevich nutzen überwiegend Rybka zur Analyse.

Inzwischen kann man hochklassiges Schach auch auf Mobiltelefonen, PDAs und sonstigen Handhelds spielen. Auf Palm-OS-basierten Geräten steht beispielsweise mit OpenChess ein freies Schachprogramm zur Verfügung, das die Auswahl zwischen mehreren Schachengines bietet.

Um Schachvarianten einmal auszuprobieren, kann das freie Programm ChessV benutzt werden.

Aufbau

Ein Schachprogramm besteht mindestens aus einem Zuggenerator, einer Bewertungsfunktion und einem Programmteil zur Steuerung der Suche und der Auswahl des nächsten Zuges. Eines der wichtigsten Unterscheidungsmöglichkeiten von Schachprogrammen ist die interne Brettdarstellung, die das Rückgrat bildet und alle anderen Bestandteile miteinander verbindet.

Zuggenerator und interne Brettdarstellung

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h

Das in allen folgenden Darstellungen verwendete Beispiel Spielstellung nach: 1. e4 e5 2. Sc3

Der Zuggenerator erzeugt, ausgehend von einem bestimmten Spielstand, eine Liste aller bei diesem Spielstand regelkonformen Antwortzüge (mögliche Bewegungen der Spielfiguren). In der Anfangsstellung sind 20 Figurenbewegungen möglich (16 Bauernzüge, 4 Springerzüge), im weiteren Spielverlauf kann man mit etwa 40 möglichen Antwortzügen pro Stellung rechnen, wobei auch komplizierte Züge wie Rochaden, Bauernumwandlungen und En-passant-Schläge zu berücksichtigen sind.

Zur Kodierung der Figuren werden hier in den Beispielen folgende ganzen Zahlen verwendet:

Figur	Kodierung
	Weiß	Schwarz
leeres Feld	0	0
Bauer	1	2
Turm	11	21
Springer	12	22
Läufer	13	23
Dame	14	24
König	10	20
ungültiges Feld	-1	-1

Die Implementierung des Zuggenerators hängt eng mit der internen Brettdarstellung zusammen. Hier gibt es drei wichtige Vertreter:

• 12x10-Darstellung

Spielstellung nach: 1. e4 e5 2. Sc3

-1 (0)	-1 (1)	-1 (2)	-1 (3)	-1 (4)	-1 (5)	-1 (6)	-1 (7)	-1 (8)	-1 (...)
-1 (10)	-1	-1	-1	-1	-1 (15)	-1	-1	-1	-1 (19)
-1 (20)	21	22	23	24	20	23	22 (27)	21	-1
-1	2	2	2	2	0 (35)	2	2	2	-1 (39)
-1	0	0	0	0	0	0 (46)	0	0 (48)	-1
-1	0	0	0	0	2	0	0	0	-1
-1	0	0	0	0	1	0	0	0	-1
-1	0	0	12	0	0	0	0	0	-1
-1	1	1	1	1	0	1	1	1	-1
-1	11	0	13	14	10	13	12	11	-1
-1	-1	-1	-1	-1	-1	-1	-1	-1	-1
-1	-1	-1	-1	-1 (...)	-1 (115)	-1 (116)	-1 (117)	-1 (118)	-1 (119)

Das Spielfeld wird auf ein eindimensionales und 120 Byte großes Array abgebildet. Zusätzlich zu den 64 Spielfeldern enthält es Felder, welche eine Figur beim Verlassen des Brettes erreichen würde und die quasi einen Rand um das reguläre Feld bilden. Da leicht abgefragt werden kann, wenn Figuren diesen Bereich betreten, ist diese Form der Darstellung sehr übersichtlich zu implementieren und macht den Zuggenerator sehr schnell (z. B. in Phalanx, ein Schachprogramm, welches man sich als Lehrbeispiel wegen seiner Übersichtlichkeit gut ansehen kann). Zu beachten ist, dass der linke und rechte Rand an jeder Seite nur ein Feld groß sein muss, da sie sich durch die eindimensionale Darstellung des Arrays zu einem Doppelfeld ergänzen. Der Index verläuft einfach von 0 (links oben) bis 119 (rechts unten).

Durch einfache Addition der folgenden Konstanten auf den Feldindex lassen sich mögliche Nachfolgepositionen bestimmen.

Bewegung	Konstanten
Horizontale und vertikale Bewegung (Turm, Dame, König)	-10, -1, +1, +10
Diagonale Bewegung (Läufer, Dame, König)	-11, -9, +9, +11
Bewegung wie ein Springer	-21, -19, -12, -8, +8, +12, +19, +21

Beispiel: Betrachten wir den Springer auf Feld 27 (Sg8). Durch die Addition der angegebenen Konstanten (siehe oben in der Tabelle) lassen sich potentielle Zielfelder bestimmen. Es sind 6, 8, 15, 19, 35, 39, 46 und 48. Ist der Wert im Feld gleich -1, dann ist der Zug nicht möglich, da der Springer zu nahe am Rand stand. Ist der Wert größer Null kann eventuell geschlagen werden. Ist er gleich Null ist ein Zug möglich (beachte noch Fesselungen und ähnliches) und er kann in die Liste der zu bewertenden Züge aufgenommen werden. Im Detail sind natürlich hier noch jede Menge an Sonderfällen zu berücksichtigen. So denke man an die unterschiedlichen Zugmöglichkeiten von Dame und König oder Fesselungen und vieles andere.

Während der Zuggenerator, der sehr einfach aufgebaut ist, schnell ist, sind die statischen Bewertungsfunktionen langsamer.

• 8x8-Darstellung

Spielstellung nach: 1. e4 e5 2. Sc3

21	22	23	24	20	23	22	21
2	2	2	2	0	2	2	2
0	0	0	0	0	0	0	0
0	0	0	0	2	0	0	0
0	0	0	0	1	0	0	0
0	0	12	0	0	0	0	0
1	1	1	1	0	1	1	1
11	0	13	14	10	13	12	11

Die 8x8-Darstellung ist der menschlichen Sicht am nächsten. Das Programm GNU Chess verwendete sie bis Version 4. Das Brett wird mit einem zweidimensionalen, acht mal acht großen Array modelliert, wobei der Index von (0;0) (links oben) bis (7;7) (rechts unten) verläuft.

Prinzipiell funktioniert bei einer 8x8-Darstellung der Zuggenerator ähnlich. Da hier die Spezialfälle am Rand aber gesondert behandelt werden müssen, ist der Zuggenerator viel komplexer. Die statische Bewertungsfunktion arbeitet allerdings schneller.

Die 0x88-Darstellung ist eine Weiterentwicklung der „8x8“ Darstellung. Von den 8 mal 16 Feldern bildet der linke Bereich von 8 mal 8 Feldern das Schachbrett, der rechte Bereich von 8 mal 8 Feldern entspricht den Randfeldern der „12x10“ Darstellung. Der Zuggenerator kann eine ungültige Position mit Hilfe der Konjunktion „&& 0x88“ ermitteln.

• Bitboards

Manche modernen Schachprogramme, etwa Rybka, Crafty oder GNU Chess 5, verwenden Bitboards. Sie sind besonders effizient auf 64-Bit-Rechnerarchitekturen. Dort ist die Anzahl der Bits eines Registers gleich der Anzahl der Spielfelder. Dadurch können diese Schachprogramme sehr schnell und effizient arbeiten, was allerdings wegen vieler Bit-Operationen im Quellcode auf Kosten der Übersichtlichkeit geht.

Spielstellung nach: 1. e4 e5 2. Sc3

Registername   0        8        16       24       32       40       48       56     63 
           |   |        |        |        |        |        |        |        |      |
Bauern     B   00000000 11110111 00000000 00001000 00001000 00000000 11110111 00000000
Türme      T   10000001 00000000 00000000 00000000 00000000 00000000 00000000 10000001
Springer   S   01000010 00000000 00000000 00000000 00000000 00100000 00000000 00000010
Läufer     L   00100100 00000000 00000000 00000000 00000000 00000000 00000000 00100100
Damen      D   00010000 00000000 00000000 00000000 00000000 00000000 00000000 00010000
Könige     K   00001000 00000000 00000000 00000000 00000000 00000000 00000000 00001000 
Farbe      F   11111111 11110111 00000000 00001000 00000000 00000000 00000000 00000000

Beispiel: Durch die Booleschen Verknüpfungen (T && !F) lassen sich jetzt alle Positionen der weißen Türme bestimmen.

Bewertungsfunktionen

Die Bewertungsfunktion liefert die Bewertung einer Stellung zurück, ohne die Nachfolgezüge zu bestimmen. Sie setzt sich aus einer materiellen und einer positionellen Komponente zusammen. Die positionelle Komponente ergänzt die materielle, da die Stärke der Spielfiguren auch von ihren Positionen untereinander abhängen. Vereinfachte Bewertungsfunktionen können auch von menschlichen Spielern ausgeführt werden, was allerdings nur eine historische Bedeutung hat. Computerprogramme zeigen sehr oft die Bewertung einer Spielsituation numerisch (in sogenannten Bauerneinheiten) an, wobei positive Werte Vorteile und negative Werte Nachteile für einen bestimmten Spieler bedeuten.

Material

Für die materielle Wertung werden für die auf dem Brett befindlichen Spielfiguren Werte addiert. Eine einfache Zuordnung ist in der folgenden Tabelle angegeben.

Bauer	Springer	Läufer	Turm	Dame
100	275	325	465	900

Für Schwarz gelten die entsprechenden negativen Werte. Der König braucht nicht mitgezählt zu werden, da beide Parteien während des gesamten Spiels jeweils einen König haben.

Position

Die positionelle Wertung zu bestimmen, ist eine Aufgabe von größerer Komplexität, in der sich die verschiedenen Schachprogramme deutlich voneinander unterscheiden. Bei kommerziellen Programmen bleibt sie ein wohlgehütetes Geheimnis. Bei der positionellen Wertung wird versucht, Stellungen aufgrund von schachrelevanten Parametern zu bewerten. Schachrelevante Parameter lassen sich grob klassifizieren in Königssicherheit, Bauernstruktur, beherrschte und bedrohte Felder sowie Figurenentwicklung. So wird zum Beispiel eine Stellung, bei der die Türme noch eingeengt zwischen Springern und Bauern stehen, schlechter bewertet als eine, bei der die Türme schon auf offenen Linien stehen.

Innerhalb dieser Kategorien gibt es quasi beliebig viele Parameter (für Bauernstrukturen zum Beispiel Freibauer, Doppelbauer, Hebel, Widder, Isolani, Bauernketten; für Königssicherheit zum Beispiel: Kann der König leicht links oder rechts rochieren? Kann er im Zentrum bleiben? Sind Bauern vor dem König?). Es bietet sich an, diese Parameter zunächst wertneutral aus der gegebenen Stellung zu extrahieren. Schachprogrammierer stehen vor der Entscheidung, wie viel Rechenzeit sie für die positionelle Komponente einer ausgefeilten Bewertungsfunktion aufwenden sollen, und welche Parameter überhaupt einfließen sollen: Je tiefer die Schachprogramme den Suchbaum analysieren können, desto eher wird nämlich die Umwandlung positioneller Vorteile in materielle Vorteile sichtbar.

Statische Bewertungsfunktion

Kann ein Schachprogramm die Werte dieser Parameter pro Stellung effizient bestimmen, müssen diese untereinander gewichtet werden. Die Gewichtung der positionellen Komponente kann teilweise automatisch über das Analysieren von Schachdatenbanken oder durch Spiele gegen andere Schachprogramme erfolgen. Geschieht dies im Vorfeld der Programmentwicklung, spricht man von einer statischen Bewertungsfunktion. Einfach aufgebaute Bewertungsfunktionen verwenden für die positionelle Komponente Positionsgewichte für die sechs Spielfigurentypen, die aber für Eröffnung, Mittel- und Endspiel jeweils unterschiedlich ausfallen.

Die Bewertungsfunktion kann außer in Grenzfällen wie Endspielen oder Matt- oder Pattsituationen keine objektiv richtigen Ergebnisse liefern. Indem die Bewertungsfunktion die materielle und positionelle Komponente zu einer einzigen Bewertungszahl zusammenfasst, ermöglicht sie aber die Sortierung und Auswahl des „besten“ beziehungsweise „schlechtesten“ Zuges.

Dynamische Bewertungsfunktion

In der Regel wird die Bewertungsfunktion vom Programmierer implementiert und während des Spieles nicht mehr verändert. Eine erweiterte Möglichkeit besteht darin, während des Spieles vergleichbare Stellungen aus einer Schachdatenbank zu ermitteln und so die Gewichtung der positionellen Parameter zu optimieren. Dies entspricht eher dem menschlichen Ansatz. Ein erfahrener Spieler berücksichtigt Kriterien wie Königssicherheit oder Freibauern auch unter Einbeziehung von ihm bekannter Partien und von deren Ergebnissen.

Steuerung der Suche und Zugauswahl

Grundsätzlich basiert die Steuerung der Suche auf dem Aufbau eines Positionsbaumes (Suchbaum) beginnend bei der aktuellen Stellung, allen Antwortzügen des Anziehenden, sowie für jeden Antwortzug aller möglichen Antwortzüge des Nachziehenden und so weiter, allein begrenzt durch die Rechenleistung und die für den Zug zur Verfügung gestellte Zeit. Jede dabei entstehende Stellung wird prinzipiell bewertet. Am Ende der Berechnung erfolgt die Zugauswahl nach dem Minimax-Algorithmus.

Da die Anzahl der zu untersuchenden Stellungen exponentiell wächst, andererseits eine höhere Suchleistung eine entsprechende Spielstärkeverbesserung hervorbringt, wurde von Programmierern in den rund 50 Jahren der Programmentwicklung ein ganzes Arsenal an Beschleunigungsmaßnahmen erfunden, die man in zwei Bereiche einteilen kann. Die einen versuchen den Suchbaum durch allgemeine Algorithmen der Informatik zu vereinfachen, so zum Beispiel:

• Alpha-Beta-Suche (Negamax-Verfahren)
• Hashtables
• Null-Zug-Suche

Die anderen verwenden intelligentere Ansätze (siehe B-Strategie), wie

• das Sortieren der Züge nach ihrer Wertigkeit,
• die Verwendung vereinfachter Bewertungsfunktionen für weniger gute Züge,
• die selektiven Erweiterungen des Suchbaums für Hauptvarianten.

Diese Algorithmen ahmen das Verhalten eines menschlichen Spielers nach und sind sehr viel schwieriger zu implementieren als die erstgenannten. Auch lassen sie sich nicht so ohne weiteres auf andere Spiele wie Go übertragen.

Bibliotheken und Datenbanken

Eröffnungsbibliothek

Schach wird im Wettkampf auf Zeit gespielt, das heißt, für eine Anzahl von Zügen steht nur eine definierte Zeit zur Verfügung. Viele Schachprogramme sind daher mit einer Eröffnungsbibliothek ausgestattet, in der sehr viele „gute“ Zugreihenfolgen in der Eröffnungsphase von Schachspielen abgespeichert sind. In der Anfangsphase des Schachspiels sieht das Programm in dieser Bibliothek nach, welcher Zug in einer bestimmten Brettstellung der geeignetste ist. Dieses „Nachsehen“ geht schneller, als den Zug auszurechnen. Die so gesparte Rechenzeit steht dem Programm dann in späteren Phasen des Spiels zur Verfügung. Das Verfahren, Brettstellungen einschließlich der „guten“ Züge abzuspeichern, ist nur für Eröffnung und Endspiel sinnvoll, da hier die Anzahl der Brettstellungen noch überschaubar ist. Eröffnungsbibliotheken kommerziell erhältlicher Programme haben derzeit eine Größe von 200 bis 250 Megabyte. Sie werden meist aus Meisterpartien generiert. Dies birgt die Gefahr, dass auch unbemerkte Fehler übernommen werden, die das Programm aus eigener Berechnung nicht spielen würde.

Einen großen Anteil an der Spielstärke hat die Abstimmung der Eröffnungsbibliothek auf die später in der Partie genutzte Bewertungsfunktion.

Endspiel-Datenbank

Im Endspiel, wenn nur noch wenige Figuren auf dem Brett sind, kann man den optimalen Zug im Vorhinein durch vollständige Analyse (Brute-Force-Methode) berechnen. Es gibt nicht wenige Endspielstellungen, in denen das menschliche Denken, aber auch die Computeranalyse in Echtzeit völlig überfordert wären. Viele Schachprogramme verwenden deshalb Endspiel-Datenbanken, die alle möglichen Stellungen mit 3, 4 oder 5 Steinen sowie deren Ausgang (bei optimalem Spiel) enthalten. Das Erstellen von Endspiel-Datenbanken geht auf Ken Thompson zurück. Die ersten Sechssteiner wurden 1991 von Lewis Stiller vollständig berechnet.

Schachdatenbank

Schachdatenbanken enthalten gespielte Partien. Sie helfen zum Beispiel beim Studium von Eröffnungen und bei der Vorbereitung auf die nächsten Gegner.

Für Schachprogramme lassen sich aus dem Datenbestand Eröffnungsbibliotheken generieren. Auch ist es möglich, während der Partie vergleichbare Stellungen aus einer Schachdatenbank zu ermitteln und unter Berücksichtigung des dort verzeichneten Partieverlaufs positionelle Bewertungsparameter (siehe oben) zu optimieren (dynamische Bewertungsfunktion).

Geschichte

Die Geschichte des Schachprogramms hängt sehr eng mit der Geschichte des Schachcomputers zusammen und lässt sich zumeist nicht getrennt behandeln. Hier werden lediglich Entwicklungen der grundlegenden Algorithmen beschrieben. Zu den in den letzten Jahren medienwirksam ausgetragenen Wettbewerben mit Weltklassespielern siehe den Artikel Computerschach.

Konrad Zuse

In den Jahren 1942 bis 1945 schrieb Konrad Zuse das weltweit erste Schachprogramm in seiner neu entwickelten Programmiersprache, dem Plankalkül. Es gab aber noch keine Compiler für diese Sprache.^[1]

Alan Turing

Alan Turing entwickelte während des Zweiten Weltkrieges in Bletchley Park ein Verfahren, welches jedem möglichen Zug einen Wert zuweist. So funktionierte Turings Schachprogramm:

• Jede Figur erhielt einen bestimmten Wert: Bauer = 1; Springer = 3; Läufer = 3,5; Turm = 5; Dame = 10 und König = 1000 (damit dieser niemals geopfert werden konnte).
• Alle weißen Züge und alle schwarzen Gegenzüge wurden untersucht. Wenn Weiß einen Schlagzug ausführen konnte, dann wurden alle Schlagzüge des Gegners, alle darauffolgenden weißen Schlagzüge usw. untersucht, bis die Stellung „tot“ war, das heißt bis es keine weiteren Schlagzüge und kein Matt gab. In den entstehenden Stellungen wurde eine Figurenzählung durchgeführt und der Zug gewählt, der das meiste Material gewann bzw. am wenigsten verlor.

Da jedoch, besonders in der Eröffnungsphase, die meisten zur Auswahl stehenden Züge das gleiche Ergebnis (+/- Null) lieferten, führte Turing auch einige positionelle Bewertungskriterien ein.

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h

Stellung nach dem 29. Zug

Die erste Partie der „Papiermaschine“ von Turing fand im Jahr 1952 statt und soll hier beispielhaft aufgeführt werden:

Turings Papiermaschine - Alick Glennie, Manchester, 1952

1. e4 e5 2. Sc3 Sf6 3. d4 Lb4 4. Sf3 d6 5. Ld2 Sc6 6. d5 Sd4 7. h4 Lg4 8. a4 Sxf3+ 9. gxf3 Lh5 10. Lb5+ c6 11. dxc6 O-O 12. cxb7 Tb8 13. La6 Da5 14. De2 Sd7 15. Tg1 Sc5 16. Tg5 Lg6 17. Lb5 Sxb7 18. O-O-O Sc5 19. Lc6 Tfc8 20. Ld5 Lxc3 21. Lxc3 Dxa4 22. Kd2 (22. h5 hätte den Laufer erobert.) 22... Se6 23. Tg4 Sd4 (23... Txb2 24. Lxb2 Txc2+) 24. Dd3 Sb5 25. Lb3 Da6 26. Lc4 Lh5 27. Tg3 Da4 28. Lxb5 Dxb5 29. Dxd6 Td8 0-1 ^[2]

Zu der „Papiermaschine“ von Alan Turing gibt es auch Implementierungen für heutige Computer.

Claude Shannon

In den Bell Laboratories hielt Claude Shannon am 9. März 1949 einen für die Entwicklung von Schachprogrammen entscheidenden Vortrag. Er beschrieb dort die interne Brettdarstellung, die Baumsuche, die Bewertungsfunktion sowie die Zugsuche mit Hilfe des Minimax-Algorithmus. Er gab auch schon zwei verschiedene Strategien zur Bestimmung des besten Zuges an: A-Strategie und B-Strategie

Dietrich Prinz

Dr. Dietrich Prinz hat 1951 für den Ferranti-Mark-I-Computer (GB) ein Matt in zwei Zügen Schachendspielprogramm erstellt.

John von Neumann

John von Neumann klassifizierte das Schachspiel in seiner Spieltheorie als Zwei-Personen-Nullsummenspiel mit vollständiger Information. Diese Klasse von Problemen (dazu gehört auch Tic Tac Toe) kann mit dem Minimax-Algorithmus gelöst werden. Schach ist jedoch zu komplex, um den Suchbaum vollständig abarbeiten zu können. Schachprogramme sind deshalb auf Näherungsverfahren angewiesen.

Grundstellung

Stellung nach dem 21. Zug

Das Schachprogramm von John von Neumann wurde Mitte der 1950er-Jahre fertiggestellt und lief auf dem 1950 aufgestellten Röhrenrechner MANIAC I. Zur Vereinfachung wurde nur auf einem 6x6-Brett gespielt. Das Programm spielte insgesamt drei Partien: Die erste gegen sich selbst, eine weitere verlor es gegen einen starken Schachspieler, obwohl dieser ihm eine Dame vorgab, und die dritte gewann es gegen eine junge Frau, die erst seit einer Woche Schach spielte und extra für dieses Spiel trainiert hatte.

MANIAC I - Mensch, Los Alamos, 1956:

(6x6-Brett ohne Läufer, kein Doppelschritt oder Rochade)

1. d3 b4 2. Sf3 d4 3. b3 e4 4. Se1 a4 5. bxa4 (5. Sd2 nebst 6. Sc4+ Sxc4 7. bxc4 mit gutem Spiel) 5... Sxa4 6. Kd2 Sc3 7. Sxc3 bxc3+ 8. Kd1 f4 9. a3 Tb6 10. a4 Ta6 11. a5 Kd5 12. Da3 Db5 13. Da2+ Ke5 14. Tb1 Txa5 15. Txb5 Txa2 16. Tb1 (Um 16...Ta1 matt zu verhindern) 16... Ta5 17. f3 Ta4 18. fxe4 c4 19. Sf3+ Kd6 20. e5+ Kd5 21. exf6 (=D) 21... Sc5 (22. Dxd4+ Kc6 23. Se5 matt.) 1-0 ^[2]

Zum ersten Mal hat ein Mensch gegen ein Schachprogramm verloren. Diese vereinfachte Schachvariante wird auch Los Alamos Chess genannt (siehe auch Schachvarianten).

1957 implementierte der IBM-Angestellte Alex Bernstein auf einer IBM 704 ein Schachprogramm, das nach den Standardregeln spielte. Es selektierte in jeder Stellung die sieben plausibelsten Züge und führte eine Suche von 4 Halbzügen durch, was ungefähr 8 Minuten Rechenzeit erforderte. Bernstein erhielt bei der Entwicklung Unterstützung durch den amerikanischen Großmeister Arthur Bisguier. Das Programm verlor chancenlos gegen den Schachmeister Edward Lasker, der dem Computer jedoch ein passables Amateurniveau bescheinigte.

1958 wurde die Alpha-Beta-Suche von Allen Newell, John Shaw und Herbert Simon entdeckt und brachte einen gewaltigen Leistungsschub.

Richard Greenblatt