Coocurrence Matrix

Die Grauwertematrix (engl. co-occurrence matrix) ist ein wichtiges Hilfsmittel in der digitalen Bildverarbeitung

Verwendet wird die Grauwertematrix bei der Erkennung von Texturen. Bei einem Bild mit kontrastreicher Oberflächenstruktur ist die linke untere und die rechte obere Ecke stark besetzt während ein Bild mit großen monotonen Flächen eine starke Hauptdiagonale hat.

Die Matrix der Graukombinationen ist: 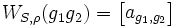${W_{S,\rho}}({g_1}{g_2})=\begin{bmatrix}{a_{{g_1},{g_2}}}\end{bmatrix}$, wobei 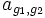$a_{{g_1},{g_2}}$ die Häufigkeit der Graukombinationen 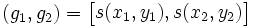$({g_1},{g_2}) = \begin{bmatrix}s({x_1},{y_1}),s({x_2},{y_2})\end{bmatrix}$ und ρ die Relation zwischen den Bildpunkten (x₁,y₂) und (x₂,y₂) beschreibt.

Zusätzlich lässt sich an den Elementen 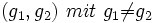$({g_1},{g_2})\ mit\ {g_1}\not={g_2}$ die ungefähre Länge der Grenze zwischen dem Grauwert g₁ und g₂ erkennen.

Beispiel

Ausgangsbild für das Beispiel, in stark vergrößerter Form. Von 0 bis 3 heller werdend.

Das Beispiel ist ein Bild mit einigen monotonen Bereichen und hat daher auch eine starke Hauptdiagonale.

$Bild\ S\ mit\ G=[0,1,2,3]: \begin{bmatrix} 0 & 1 & 0 & 1 & 2 & 3 \\ 0 & 0 & 1 & 2 & 2 & 2 \\ 0 & 0 & 1 & 1 & 1 & 2 \\ 0 & 1 & 2 & 2 & 3 & 3 \\ 0 & 2 & 2 & 3 & 3 & 3 \\ 2 & 2 & 2 & 3 & 3 & 3 \\ \end{bmatrix}$

$Und\ Relation\ \rho\ mit:\ \rho(x,y) = (x+1, y)$

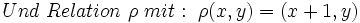
ergibt die Grauwertematrix

${W_{S,\rho}}({g_1},{g_2}) = \begin{bmatrix} 2 & 5 & 1 & 0 \\ 1 & 2 & 4 & 0 \\ 0 & 0 & 6 & 4 \\ 0 & 0 & 0 & 5 \\ \end{bmatrix}$

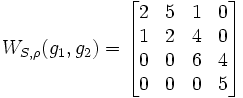
Literatur

• Peter Haberäcker: Digitale Bildverarbeitung, Hanser Verlag