Cost Balancing Concept

Die optimale Bestellmenge bezeichnet innerhalb der Beschaffungslogistik jene Menge, bei der die Summe aus den fixen und variablen Bestell- sowie Lagerhaltungskosten für einen vorgegebenen Servicegrad im Planungszeitraum ein Minimum aufweist.

Je häufiger bestellt wird, umso höher sind die Bestellkosten und umso niedriger die Lagerhaltungskosten. Bei einer geringeren Bestellhäufigkeit sind die Lagerhaltungskosten höher und die Bestellkosten niedriger. Die optimale Bestellmenge ist erreicht, wenn die Summe aus Bestell- und Lagerhaltungskosten am geringsten ist.

Bestellkosten

Die Bestellkosten enthalten die gesamten Abwicklungskosten einer Bestellung, von der Bestellvorbereitung über den Bestellabschluss bis zur Bestellabwicklung. Oft sind die Bestellkosten pro Einheit abhängig von der Bestellmenge, beispielsweise aufgrund von Rabatten bei Abnahme größerer Mengen.

Bestellkosten pro Bestellung = Summe der Bestellkosten pro Periode / Anzahl der Bestellungen pro Periode

Lagerhaltungskosten

Die Lagerhaltungskosten umfassen die Kosten für das Personal, die Lagerräume und das gebundene Kapital, inklusive Kosten für Wertminderung durch Schwund, Veralterung etc., und die Versicherung von Vorräten und Räumen.

Lagerhaltungskostensatz = Zinssatz des gebundenen Kapitals + Lagerkostensatz

Statische Bestellmengenrechnung (Klassische Losformel)

Statische Bestellmengen bedeuten, dass eine "Optimale" Bestellmenge bestimmt wird, welche dann immer in diesem Volumen bestellt wird. Es handelt sich um die frühesten Überlegungen, das Losgrößenproblem zu lösen. Siehe Hauptartikel: Klassische Losformel.

Lagerkennziffern

durchschnittlicher Lagerbestand = (Jahresanfangsbestand+Jahresendbestand)/2
Lagerumschlagshäufigkeit = Jahresbedarf/durchschnittlicher Lagerbestand
durchschnittliche Lagerdauer = 360/Lagerumschlagshäufigkeit
Lagerzinssatz = (durchschnittliche Lagerdauer*Jahreszinssatz)/360

Kostenverlauf grafisch darstellen

weitere Formel aus der Finanzmathematik: 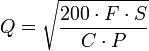$Q=\sqrt{{200 \cdot F \cdot S}\over{C \cdot P}}$ mit:

Q	optimale Bestellmenge bei jeder neuen Order
F	Kosten pro Jahr
S	Jahresumsatz
C	Bestandhaltungskosten in %
P	Kaufpreis

Dynamische Bestellmengenrechnung

Verfahren der dynamischen Bestellmengenrechnung werden verwendet, wenn der zukünftige Bedarf nicht konstant ist, d.h. starken Schwankungen unterliegt. Das Optimum wird bei diesen Verfahren nicht analytisch, sondern durch eine schrittweise Näherung errechnet, was in der Praxis meistens ausreicht. Im Folgenden werden nun verschiedene Verfahren vorgestellt.

Gleitendes wirtschaftliches Bestellmengenverfahren

Beim gleitenden wirtschaftlichen Bestellmengenverfahren wird der Bedarf in Teilperioden gegliedert, das Optimum liegt in der Gesamtperiode mit den geringsten Stückkosten. Die Periodenbedarfe werden so lange kumuliert, bis die Stückkosten wieder steigen.

Optimale Bestellmenge = kumulierter Bedarf bis zu jener Teilperiode, für die ein Minimum gilt von:

(Bestellkosten + kumulierte Lagerhaltungskosten) / kumulierter Bedarf

Beispiel

Bestellkosten: 90 GE

Lagerhaltungskosten pro Stück und Monat: 0,2 GE

Berechnung der Bestell- und Lagerhaltungskosten/Stück:

1. Periode: (90 + 120 x 0,5 x 0,2) / 120 = 0,85

2. Periode: (90 + 120 x 0,5 x 0,2 + 38 x 1,5 x 0,2) / (120 + 38) ≈ 0,72 usw.

Monat	Bedarf (Stk.)	Bestellmenge (Stk.)	Lagerdauer (Monate)	Lagerhaltungskosten/Monat	Kum.	Bestellkosten	Bestell- u. Lagerhaltungskosten/Stk.
1	120	181	0,50	120 x 0,50 x 0,20 = 12	12	90	102 / 120 = 0,85
2	38		1,50	38 x 1,50 x 0,20 = 11,40	23,40		113,40 / 158 = 0,72
3	15		2,50	15 x 2,50 x 0,20 = 7,50	30,90		120,90 / 173 = 0,70
4	8		3,50	8 x 3,50 x 0,20 = 5,60	36,50		126,50 / 181 = 0,70
5	60		4,50	60 x 4,50 x 0,20 = 54	90,50		180,50 / 241 = 0,75
5	60		0,50	60 x 0,50 x 0,20 = 6	6	90	96 / 60 = 1,60
6	3		1,50	3 x 1,50 x 0,20 = 0,90	6,90		96,90 / 63 = 1,54
7	75		2,50	75 x 2,50 x 0,20 = 37,50	44,40		134,40 / 138 = 0,97
…

Ab der 5. Periode steigen die Stückkosten wieder, daher lohnt es sich nicht diesen Bedarf zu Beginn der 1. Periode einzulagern. Die optimale Bestellmenge in der 1. Periode beträgt daher 181 Stück. Mit der 5. Periode beginnt der Rechenprozess von neuem, bis zum nächsten Minimum.

Kostenausgleichsverfahren

Im Kostenausgleichsverfahren wird der Punkt ermittelt, in dem Bestell- und Lagerhaltungskosten ungefähr gleich hoch sind. Beim Rechenvorgang wird die Bestellmenge so lange erhöht, bis die kumulierten Lagerhaltungskosten die Bestellkosten überschreiten.

Optimale Bestellmenge = kumulierter Bedarf bis zur Teilperiode, für die gilt:

Kumulierte Lagerhaltungskosten ≈ Bestellkosten

Beispiel

Monat	Bedarf (Stk.)	Bestellmenge (Stk.)	Lagerdauer (Monate)	Lagerhaltungskosten/Monat	Kum.	Bestellkosten
1	120	241	0,50	120 x 0,50 x 0,20 = 12	12	90
2	38		1,50	38 x 1,50 x 0,20 = 11,40	23,40
3	15		2,50	15 x 2,50 x 0,20 = 7,50	30,90
4	8		3,50	8 x 3,50 x 0,20 = 5,60	36,50
5	60		4,50	60 x 4,50 x 0,20 = 54	90,50
6	3		0,50	3 x 0,50 x 0,20 = 0,30	0,30	90
7	75		1,50	75 x 1,50 x 0,20 = 22,50	22,80
…

Bei der Bestellung in der 1. Periode wird für die Perioden 1-5 bestellt, weil bei Miteinbezug des Bedarfes der 6. Periode die Lagerhaltungskosten die Bestellkosten schon übersteigen. Die optimale Bestellmenge beträgt 241 Stück.

Kostenausgleichsverfahren mit Look-ahead

Beim Kostenausgleichsverfahren kann es passieren, dass ein sehr kleiner Bedarf, der sehr niedrige Lagerhaltungskosten verursacht, eine Bestellung auslöst. Um Kosten zu sparen, kann daher eine Look-ahead-Abfrage angewandt werden. Mit Anwendung dieser Methode wird überprüft, ob eine Verschiebung des ersten Teilbedarfes einer Bestellperiode in die vorangegangene Periode niedrigere Lagerhaltungskosten verursacht. Ein Look-ahead kann auch bei anderen Verfahren angewendet werden.

Beispiel

Woche	Bedarf (Stk.)	Bestellmenge (Stk.)	Lagerdauer (Wochen)	Lagerhaltungskosten/Wochen	Kum.	Bestellkosten
1	120	244	0,50	120 x 0,50 x 0,20 = 12	12	90
2	38		1,50	38 x 1,50 x 0,20 = 11,40	23,40
3	15		2,50	15 x 2,50 x 0,20 = 7,50	30,90
4	8		3,50	8 x 3,50 x 0,20 = 5,60	36,50
5	60		4,50	60 x 4,50 x 0,20 = 54	90,50
6	3		5,50	3 x 5,50 x 0,20 = 3,30	3,30
7	75		0,50	75 x 0,50 x 0,20 = 7,50	10,80	90
…

Mit einem Look-ahead erreicht man hier eine Kostenersparnis von 12 GE, da der Bedarf der 6. Periode bei der ersten Bestellung miteinbezogen wird: (0,30 + 22,50) - (3,30 + 7,5) Die optimale Bestellmenge beträgt 244.

Stück-Perioden-Ausgleichsverfahren

Auch beim Stück-Perioden-Ausgleichsverfahren wird das Optimum dadurch ermittelt, dass der Punkt errechnet wird, in dem Bestell- und Lagerhaltungskosten etwa gleich hoch sind. Im Gegensatz zum Kostenausgleichsverfahren ist jedoch eine tagesgenaue Berechnung der Bestellmenge möglich.

Zuerst müssen die spezifischen Lagerhaltungskosten je Stück und Periode errechnet werden.

Spezifische Lagerhaltungskosten = Lagerhaltungskosten / Stück x Tage

Der Quotient aus Bestellkosten und spezifischen Lagerhaltungskosten ergibt die optimalen Stück-Tage.

Optimale Stück-Tage = Bestellkosten / spezifische Lagerhaltungskosten

Ein Wert von 100 Stück-Tagen bedeutet, dass 2 Stück in 50 Tagen die gleichen Lagerhaltungskosten verursachen wie 50 Stück in 2 Tagen.

An dem Punkt, an dem die errechneten Stück-Tage überschritten werden, ist die optimale Bestellmenge erreicht.

Beispiel

Einstandspreis: 10; Lagerhaltungskostensatz: 24%; Bestellkosten: 90; Periode: 20 Fabriktage pro Monat SLHK = 10 x 0,24 / 240 = 0,01; Optimale Stück-Tage = 90 / 0,01 = 9000

Fabriktage	Bedarf (Stk.)	Bestellmenge	Lagerdauer (Monate)	Stück-Tage	Kum.	Optimale Stück-Tage-Menge
20	120	241	0,50	20 x 120 x 0,50 = 1200	1200	9000
20	38		1,50	20 x 38 x 1,50 = 1140	2340
20	15		2,50	20 x 15 x 2,50 = 750	3090
20	8		3,50	20 x 8 x 3,50 = 560	3650
20	60		4,50	20 x 60 x 4,50 = 5400	9050
20	3		0,50	20 x 3 x 0,50 = 30	30	9000
20	75		1,50	20 x 75 x 1,50 = 2250	2280
…

Die optimale Stück-Tage-Menge wird in der 5. Periode leicht überschritten. Die optimale Bestellmenge beträgt daher 241 Stück.

Das Losgrößenmodell von Wagner und Whitin

Wird auch als Kürzeste-Wege-Verfahren (Wagner-Whitin-Algorithmus) bezeichnet und gehört den dynamischen (Periodenbedarf schwankt) Modellen der Losgrößenplanung an. Der Planungszeitraum wird in diskrete Perioden unterteilt. Dabei ist die Höhe der Bedarfsnachfrage aus jeder Periode bekannt.

Bei periodenweiser Produktion fallen (bekannte) Rüstkosten an und die Nachfrage wird aus der laufenden Produktion oder aus dem Lagerbestand (keine Fehlmengen) abgeleitet.

Problem

Zielkonflikt zwischen Beschaffungskosten und Lagerkosten:

• werden in geringen Zeitabständen kleine Mengen eingekauft so resultieren steigende Beschaffungskosten (fixe Bestellkosten, keine Rabatte)
• werden in großen Zeitabständen große Mengen eingekauft so resultieren steigende Lagerkosten (großer Lagerbestand, hohe Kapitalbindung)

Mängel des Modells

Das Modell der Optimalen Bestellmenge ist ein theoretischer Ansatz und bildet nicht die Realität ab. Für die Bedürfnisse in der Praxis ist dieses Modell somit zu knapp gehalten. Damit das Modell in der Theorie funktioniert, gelten die folgenden Prämissen:

• der Bedarf je Periode bekannt und bleibt im Zeitablauf gleich groß
• die Lagerabgangsgeschwindigkeit ist konstant
• die Auffüllzeit für das Lager ist = 0, somit ist die Auffüllgeschwindigkeit unendlich hoch
• es sind keine Fehlmengen vorhanden
• es wird nur ein Lager mit unbegrenzter Kapazität betrachtet
• der Lagerkostensatz ist der Höhe nach bekannt und bleibt konstant
• Bestellvorgänge verursachen lediglich bestellfixe Kosten
• der Einstandspreis der Güter ist konstant
• Änderungen in Güte und Qualität sind ausgeschlossen

Des Weiteren sind in der Realität innerhalb einer Planungsperiode nur ganzzahlige Lösungen möglich. Vernachlässigt wird unter anderem auch möglicher Schwund und Verfall von Gütern. Mengenrabatte und Teillieferungen sowie Bildung von Sicherheitsbeständen sind im Modell auch nicht berücksichtigt.

Siehe auch

• Bestellung
• Bestellzeitpunkt
• Stückkosten
• Einstandspreis
• Andler-Formel
• Bestellrhythmusverfahren
• Bestellpunktverfahren
• Beschaffungslogistik
• Materialwirtschaft

Literatur

• Horst Hartmann: Materialwirtschaft. Dt. Betriebswirte- Verlag. Gernsbach 2002, ISBN 3886400948
• Oskar Grün: Industrielle Materialwirtschaft. In: Marcell Schweitzer (Hrsg.): Industriebetriebslehre. 2. Auflage. München 1994, S.447-568, ISBN 3-8006-1755-2