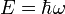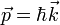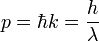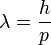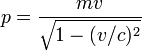De-Broglie-Welle

Materiewellen wurden 1924 von Louis-Victor de Broglie postuliert, der damit den Welle-Teilchen-Dualismus zum allgemeinen Prinzip erhob. Nach der Entdeckung der Quantelung des Lichts durch Albert Einstein bei der Untersuchung des Photoeffekts entstand das Dilemma, ob Licht als Welle oder Teilchenstrom beschrieben werden soll. Dabei entstand der Begriff des Welle-Teilchen-Dualismus. Louis de Broglie folgerte, wenn Photonen Teilchen- und Wellencharakter zeigen, dass dann auch klassische Teilchen ein solches Verhalten zeigen müssten.

In der Quantenmechanik wird davon ausgegangen, dass ein Quant keinen fest definierbaren Ort hat. Es ist nur möglich, eine Aufenthaltswahrscheinlichkeit anzugeben, die durch eine Wahrscheinlichkeitswelle beschrieben wird. Die Wahrscheinlichkeitswelle muss einer Wellengleichung folgen (zum Beispiel Schrödingergleichung oder Dirac-Gleichung). Eigenschaften, die man sonst klassischen Teilchen zuordnet, werden mit Wellenpaketen erklärt.

Siehe auch: bornsche Wahrscheinlichkeitsinterpretation

1927 gelang Clinton Davisson und Lester Germer der Nachweis der Welleneigenschaften von Elektronen durch Interferenzversuche an einem Nickel-Einkristall. De Broglies Wellenlängenformel fand dabei Bestätigung. Noch eindrucksvoller ist der Doppelspaltversuch mit Elektronen, den Claus Jönsson 1960 an der Universität Tübingen realisierte. Ähnliche Interferenzexperimente existieren mittlerweile für weitere Elementarteilchen, für ganze Atome und sogar Moleküle. Für seine Theorie erhielt Louis de Broglie 1929 den Nobelpreis für Physik.

Die De-Broglie-Wellenlänge

Nach de Broglie kann einem Teilchen eine Welle zugeordnet werden, die durch die Wellenlänge λ charakterisiert werden kann. Wir betrachten als Beispiel das Photon, das in der Maxwellschen Theorie des Elektromagnetismus als Wellenpaket interpretiert werden kann. Ein Photon besitzt keine Ruhemasse, aber Energie E und einen Impuls p :

$E = \hbar\omega$

und

$\vec{p} = \hbar \vec{k}$

Dabei ist 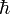$\hbar$ das reduzierte Plancksche Wirkungsquantum, ω die Kreisfrequenz und 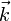$\vec{k}$ der Wellenvektor der Materiewelle. Für den Impuls eines Photons ergibt sich wegen der Definition des reduzierten Planckschen Wirkungsquantums auch ein Ausdruck für die Wellenlänge λ:

$p = \hbar k = \frac{h}{\lambda}$

Louis de Broglie verallgemeinerte diese Gleichung für beliebige Teilchen:

$\lambda = \frac{h}{p}$

wobei p hier für den relativistischen Impuls des Teilchens steht^[1]:

$p = \frac{mv}{\sqrt{1-(v/c)^2}}$

Mit der Wellenlänge λ können Streuverhalten und Interferenz von Teilchen erklärt werden. Die Wellenlänge und damit die Größe der beobachteten Effekte hängt von der Geschwindigkeit und der Masse des Teilchens ab. Deswegen sind Materiewellen nur bei sehr schweren oder schnellen Teilchen (zum Beispiel Elektronen) leicht zu beobachten. Durch Interferenzexperimente mit Fullerenen wurde die Gültigkeit der Theorie der Materiewelle auch für größere Moleküle nachgewiesen.

Quellen

1. ↑ Licht und Materie, Louis de Broglie, H. Goverts Verlag Hamburg 1939, S.163

• Broglie, Louis de, The wave nature of the electron, Nobel Lecture, December 12, 1929

• Siehe auch: Thermische De-Broglie-Wellenlänge